Связь экономики и физики: Аналогии между поведением цен на рынке и теорией колебаний

Данная заметка является продолжением публикаций: Аналогии экономики с термодинамикой и механикой

                                                                                           Связь экономики и физики: Метод научного познания 

                                                                                           Связь экономики и физики: Аналогии между механикой и микроэкономикой

Эти публикации являются популярным изложением книги: И.Г.Царев Математика и физика для экономистов.

В этой заметке мы рассмотрим поведение цен на рынке. Сразу хочу сказать всем любителям биржевых спекуляций, я не считаю возможным давать прогнозы или предсказания поведения цен. С моей точки зрения прогнозировать эти изменения можно с тем же успехом, как предсказывать мелкие и большие землетрясения земной коры при помощи уравнений Ньютона. В этой заметке я попробую построить некую общую модель, при помощи которой можно будет «понять и объяснить» некоторые черты поведения цен на рынках, а также решить возникающие при этом затруднения.

Эта заметка является продолжением дискуссии, разгоревшейся при обсуждении предыдущей статьи, и ее написание является отступлением от плана публикаций. Напомню суть дискуссии. Мой оппонент утверждал, что цены являются «фантазией», «виртуальной реальностью», «обманом», что цены не имеют отношения к товару, а является субъективным представлением каждого отдельного человека и их следует исключить из модели «реальной экономики». Я, в свою очередь, считал нелепой гипотезу, что товары вступают в процесс обращения без цены, и  более того, полагал неправильным придумывать экономику без цен, а деньги без стоимости, так как цена объективна, а субъективны представления людей о её величине. Исчерпав «философские» аргументы, что моя гипотеза «шизофренична» и, по сути, является «бредом сумасшедшего», оппонент заявил, что если моя модель не в состоянии делать прогнозы, то «её практическая ценность равна нулю», а я «развел бурю в стакане воды». Я напомнил, что теория вероятностей и математическая статистика также не способны делать прогнозы на выигрыш в казино, о чем «выпускник МФТИ, МГУ и плехановки» не может не знать. Но это не повод считать, что практическая ценность этих дисциплин равна нулю, а создавшие их математики развели бурю в стакане воды. После этого я был обвинен в переходе на личности, и дискуссия завершилась.

Столь бурно обсуждаемая проблема заслуживает более подробного освещения.

Самое первое затруднение экономической науки заключается в том, чтобы обосновать право на свое существование. В отличие от взаимодействия природных объектов экономика сталкивается с тем, что в ней взаимодействуют экономические субъекты, которые имеют свои субъективные представления о характере этих взаимодействий. Помимо субъективных экономических отношений, в которые вступают экономические субъекты, они еще имеют субъективные представления о таком свойстве экономических объектов, как их цена. Разрешение противоречия между объективностью цены и субъективными представлениями о ней участников рынка будет первой нашей задачей.

Тот факт, что цены претерпевают значительные изменения, не только не подвергается сомнению в экономической науке, но и является основой существования фондового рынка. Классическое утверждение А. Маршалла заключается в следующем: «Когда спрос и предложение пребывают в равновесии, количество товара, производимого в единицу времени, можно назвать равновесным количеством, а цену, по которой он продается, равновесной ценой. Такое равновесие является устойчивым, т.е. цена при некотором отклонении от него будет стремиться к возвращению в прежнее положение подобно тому, как маятник колеблется в ту и другую сторону от своей низшей точки».

Однако причина этих постоянных колебаний обойдена вниманием экономистов и подробно не рассматривается. Обычно экономисты считают достаточным объяснение, что колебания цены связаны со случайными актами обмена. Но ведь если эти колебания не затухают со временем в точке равновесия, значит точка равновесия на самом деле не является устойчивой. В то же время колебательное движение происходит не произвольно, а вокруг этой самой неустойчивой равновесной точки, т.е. само движение – устойчиво. Таким образом, второй нашей задачей будет «понять и объяснить» что заставляет цены колебаться.

Обычный диапазон колебания цены укладывается в несколько процентов относительно среднего значения. Таким образом, в случае «общего положения» (т.е. в большинстве случаев, за исключением некоторых особых) цены колеблются «не очень сильно». В теории колебаний такой случай общего положения называется мягкой потерей устойчивости – когда точка равновесия неустойчива, а устойчивы небольшие колебания около этой точки. В качестве третьей задачи мы выпишем характерные математические уравнения для этого случая.

В некоторых особых случаях происходит жесткая потеря устойчивости, когда система скачком большой амплитуды переходит к новой равновесной точке и начинает совершать колебания уже вокруг этого нового положения равновесия. Подобное поведение цен характерно для внезапных кризисных явлений, каким был, например, скачок доллара к рублю после знаменитого выступления Сергея Кириенко в августе 1998 года. Такой внезапный ответ системы на плавное изменение внешних условий называется в теории колебаний также катастрофой. При этом говорят, что один из параметров  системы при своем плавном изменении перешел через критическое значение. Уравнения для случая жесткой потери устойчивости будут нашей четвертой задачей.

1. Для решения первой задачи – разрешения противоречия между объективностью цены и субъективными представлениями о ней участников рынка предположим, что цена экономического объекта определяется двумя параметрами. Первый объективный параметр называется стоимостью или овеществленным в экономическом объекте трудом. Второй субъективный параметр является неким консолидированным представлением людей о величине этой стоимости.

Как один из вариантов объединить эти два параметра в одном выражении – записать цену в виде комплексного  числа z в показательной форме:

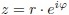
где модуль комплексного числа r – стоимость (овеществленный труд), аргумент φ – представления людей о величине этой стоимости.

Может показаться странным, что переменные величины, которыми мы собираемся обозначать цены благ, могут принимать мнимые значения. Однако даже ближайшее рассмотрение марксистской трактовки цены показывает, что дедушка Маркс интуитивно чувствовал этот характер цены: «Цена, или денежная форма товаров, как и вообще их стоимостная форма, есть нечто, отличное от их чувственно воспринимаемой вещественной формы, следовательно, – форма лишь идеальная, существующая лишь в представлении» [Маркс, Капитал, Т.I, с. 105]. «Следовательно, возможность количественного несовпадения цены с величиной стоимости … заключена уже в самой форме цены. …

Но форма цены не только допускает возможность количественного несовпадения величины стоимости с ценой, т.е. величины стоимости с ее собственным денежным выражением, – она может скрывать в себе качественное противоречие, вследствие чего цена вообще перестает быть выражением стоимости, хотя деньги представляют собой лишь форму стоимости товаров. Вещи, которые сами по себе не являются товарами, например совесть, честь и т.д., могут стать для своих владельцев предметом продажи и, таким образом … приобрести товарную форму. Следовательно, вещь формально может иметь цену, не имея стоимости. Выражение цены является здесь мнимым, как известные величины в математике. С другой стороны, мнимая форма цены – например цена не подвергавшейся обработке земли, которая не имеет стоимости, так как в ней не овеществлен человеческий труд, – может скрывать в себе действительное стоимостное отношение или отношение, производное от него» [Маркс, Капитал, Т.I, с. 112]. «В выражении стоимость труда понятие стоимости не только совершенно исчезает, но и превращается в свою противоположность. Это такое же мнимое выражение, как, например, стоимость земли. Но такие мнимые выражения возникают из самих производственных отношений» [Маркс, Капитал, Т.I, с. 547].

2. Чтобы «понять и объяснить», какая сила заставляет цены колебаться, нужно вспомнить следующее положение «теории колебаний»: чтобы в системе возникли автоколебания, т.е. собственные периодические незатухающие колебания, необходимо наличие обратной связи, которая придает системе способность управлять поступающей извне энергией. Форма, амплитуда и частота колебаний при этом задаются самой системой. Следовательно, нам необходимо сделать некие предположения, которые смогли бы объяснить появление необходимых и достаточных условий для возникновения этих самых автоколебаний в экономической системе.

Источником энергии в экономике, без сомнения, является труд, а равновесное значение цены объекта, вокруг которого происходят колебания, является стоимостью. При этом смысл обратной связи в экономической системе, видимо, состоит в том, что участники рынка пытаются понять ситуацию, возникающую на рынке, и предпринять выгодные с их точки зрения действия. Это взаимодействие, в котором как ситуация, так и взгляды участников являются зависимыми переменными, называется, по терминологии Д. Сороса, «рефлексивностью». В качестве термина им использовано слово, которое французы употребляют для обозначения глагола, субъект и объект которого совпадают.

Запишем в качестве примера уравнения колебаний простейшей динамической системы, которая называется «математический маятник». Представим себе маленький грузик, который подвешен на невесомом стержне длиной R. Будем считать, что грузик совершает малые колебания x около своей точки равновесия, т.е. отклоняется от этой точки «не очень сильно» и x<<R. Если для простоты рассмотрения мы примем, что невесомый стержень имеет единичную длину, то получим выражение для малых колебаний: x<<1.

Величина отклонения от точки равновесия грузика x является нашей первой координатой, которая характеризует колебания системы «маятник». Как мы знаем из заметки «Метод научного познания» для перехода от механической системы «математический маятник» к динамической системе, нам для полного определения системы нужно выбрать вторую координату фазового пространства y, которая будет аналогом импульса или скорости движения грузика. При этом для простоты рассмотрения поместим начало координат нашей фазовой плоскости (двумерного фазового пространства) в точку равновесия грузика. Так как грузик совершает периодические колебания, то закон изменения координат фазового пространства удобно записать в следующем виде:

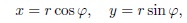
где φ называется «фазой» или «состоянием» нашей динамической системы.

При отсутствии трения фазовая траектория движения динамической системы «маятник» на плоскости x, y будет представлять собой замкнутый цикл с центром в начале координат (точке равновесия грузика). Длина радиус-вектора r является расстоянием от начала координат, до выбранной точки на этом цикле, а величина φ задает угол между осью абсцисс и радиус-вектором r. Площадь внутри замкнутого цикла является координатой действие I, а координатой угол является φ. Координаты x, y можно перевести в координаты действие угол I, φ при помощи так называемого «канонического преобразования» координат. Однако в данном случае неудобно рассматривать в качестве координаты «площадь», и мы при каноническом преобразовании будем переходить к координатам r, φ.

Если теперь представить нашу фазовую плоскость комплексной плоскостью, то мы можем объединить две наших фазовых координаты, записав комплексное число z, которое является точкой на цикле колебаний математического маятника или «состоянием динамической системой маятник»:

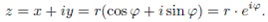
В результате мы получили то самое выражение, которые приняли выше для обозначения цены произвольного экономического объекта.

При отсутствии «трения» динамическая система маятник в разных переменных может быть записана в следующем виде:

Решение системы:

Если в системе возникает «коэффициент трения» γ (некое сопротивление среды), то в правой части к «силам тяжести» ωx и ωy добавляются «силы трения» γx, γy (или γr):

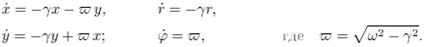
Решение системы:

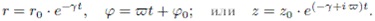
Подставив одно уравнение в другое, мы получим эквивалентное этим двум уравнениям первого порядка одно, так называемое, каноническое уравнение второго порядка для математического маятника с трением:

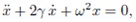
где выражение 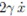  характеризует «силу трения», а выражение ω²x – «силу тяжести». 

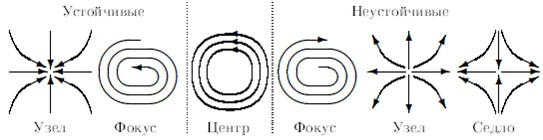
Выясним теперь поведение фазовых кривых при различном соотношении «параметров» системы: γ, ω.

Если система имеет «отрицательную силу тяжести» ω² < 0, то начало координат системы перестает быть «устойчивой точкой равновесия», а превращается в так называемую «параболическую точку» или седло (образ соответствует седловине горного хребта). Такое состояние нашей динамической системе соответствует верхнему положению маятника (когда невесомый стержень с грузиком на конце направлен строго вверх). Понятно, что любой толчок приведет к необратимому уходу системы из состояния неустойчивого равновесия, а фазовые кривые являются половинками координатных осей и гипербол и уходят на бесконечность.

В системах, где «сила трения положительна» γ > 0, будет происходить «затухание колебаний», а грузик под действием силы тяжести будет стремиться к «устойчивой» точке равновесия. В системах, где «сила трения отрицательна» γ < 0, будет происходить «раскачивание колебаний», а точка равновесия станет «неустойчивой».

Если γ = 0, то, как мы уже знаем, система совершает периодические колебания вокруг точки равновесия, фазовые кривые являются замкнутыми циклами (одномерным тором), а точка равновесия называется особой точкой типа центр.

Если 0 < γ² < ω­_­², то фазовые кривые будут представлять собой «логарифмические спирали». В зависимости от положительного или отрицательного значения коэффициента трения γ будет происходить «экспоненциальное затухание» или «экспоненциальное раскачивание» колебаний, фазовые кривые будут «накручиваться» на точку равновесия или, наоборот, «раскручиваться» из нее. А сама точка равновесия будет называться устойчивым (или неустойчивым) фокусом.

И наконец, если γ² > ω² > 0, то затухание (раскачивание) системы будет происходить очень быстро (быстрее, чем успевает произойти колебание). В зависимости от знака трения фазовые кривые будут сходиться (расходиться) к точке равновесия, которая будет называться устойчивый (неустойчивый) узел.

Как показал еще А. Пуанкаре, поведение фазовых кривых (фазовый портрет) в окрестности положения равновесия на фазовой плоскости в системах общего положения (т.е. в большинстве систем) ограничивается перечисленными случаями:

Положительной силой трения γ > 0 в экономической системе могут являться транзакционные издержки – издержки экономических субъектов по заключению контрактов. Транзакционные издержки в экономическую теорию ввел Рональд Коуз. Отрицательной силой трения γ < 0 в экономической системе могут являться «неверные» представления или ожидания участников рынка. При возникновении «паники» на рынке может появиться «отрицательная сила тяжести» ω² < 0, и произойдет «обрушение» системы биржевых торгов.

3. «Динамическую систему цена» можно записать в «более общем виде»:

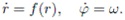
Функция f (r), находящаяся в правой части первого уравнения, может быть исследована разложением в ряд при помощи «метода Ньютона», о котором упоминалось в заметке «Метод научного познания». В данном случае речь идет о том, что эту функцию можно разложить в степенной «ряд Тейлора», который был изобретен Ньютоном и опубликован его учеником Тейлором. Так как мы рассматриваем колебания в окрестности точки равновесия, то как было сформулировано выше r << 1. Поэтому в первом приближении колебания цен хорошо описываются «системой маятник». Добавление следующих членов степенного ряда «увеличивает точность» описания системы. В теории колебаний установлено, что для описания систем типа «осциллятор» значение имеют только члены ряда с нечетными степенями.

Как мы знаем, для того чтобы равновесная цена «потеряла устойчивость» нам в окрестности точки равновесия необходим «неустойчивый фокус». Однако, размах «устойчивых колебаний» около точки равновесия должен быть «не очень большой». Этот тип колебаний называется мягкой потерей устойчивости и характерен для поведения цен на рынках.

Рассмотрим динамическую систему следующего типа:

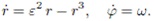
В данном случае размерность r выбрана таким образом, чтобы коэффициент при кубическом члене уравнения r³ был равен единице. Таким образом, мы ввели еще одну «силу» в нашу динамическую систему, которая имеет кубическую зависимость от диапазона колебания цены около точки равновесия. Назовем эту силу коллективными «опасениями» участников рынка, которые особенно проявляются тогда, когда диапазон колебаний цены r становится слишком велик.  Когда значения r достаточно маленькие, то кубический член практически не дает вклада в движение системы, а поведение системы определяется «неустойчивым фокусом» ε² r.

Если мы запишем уравнение:

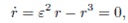
то вычислив его корни r­_i­, мы отыщем возможные «равновесные состояния» нашей «динамической системы цена». Нетрудно заметить, что кроме r­_0­ =0 таким корнем будет величина r­_1­ = ε. Это означает, что вклад кубического члена уравнения становится существенным и система достигает новой точки равновесия – так называемого предельного цикла с радиусом r­_1­ = ε.

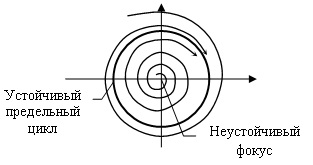
Раскручивающиеся из начала координат неустойчивые фокусы будут наматываться на цикл радиуса ε «изнутри». За пределами этого цикла ситуация меняется на противоположную, – основной вклад в движение системы дает уже кубический член r³. В результате образуется «устойчивый фокус», который наматывается на цикл радиуса ε «снаружи». Таким образом, при превышении «коэффициента отрицательного трения» γ­₂ в виде «неверных ожиданий» участников рынка над «коэффициентом положительного трения» γ­₁ в виде транзакционных издержек система цена обретает колебания диапазона ε² = γ­₂ – γ­₁, который задается разницей этих коэффициентов. При этом колебания цены стабилизируются в данном диапазоне из-за «опасений» участников рынка при слишком больших колебаниях цены.

Этот тип системы называется автоколебательной системой, а процесс называется мягкой потерей устойчивости динамической системы цена.

4. Рассмотрим теперь ситуацию, когда динамическая система цена получает очень сильный одномоментный «толчок» в виде некого действия или заявления крупного политика или чиновника. В этом случае «опасение» участников рынка меняет знак на противоположный. Теперь уже большинство участников уверены, что цена обязательно «прыгнет за флажки» привычного диапазона и стабилизируется на каком-то другом уровне. Это состояние системы называется жесткая потеря устойчивости и описывается уравнением:

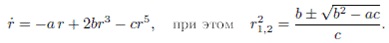
Возникновение такой ситуации в системе цена возможно при определенных значениях параметров системы a, b и c (все значения параметров положительны). Если вынести r за скобки, то в скобках получится обычное квадратное уравнение -a+2bx-cx², с r²=x. Если при вычислении корней квадратного уравнения дискриминант ac – b² будет отрицательным, то система приобретает два новых цикла, из которых маленький называется неустойчивый предельный цикл, а большой – устойчивый предельный цикл:

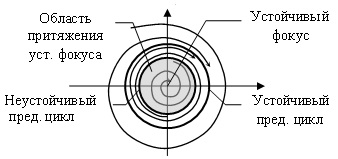
При «обычных условиях» эта система никак себя не проявляет, так как даже теоретически возможные движения системы около положения равновесия гасятся транзакционными издержками. При «толчке» больше чем r­_1­ «опасения» участников рынка стабилизируют систему в районе r­­_­2­. Таким образом, фазовый портрет системы состоит из трех областей. Расположенные «внутри» маленького цикла фазовые траектории сматываются с него и наматываются на начало координат. Фазовые траектории «между циклами» сматываются с маленького и наматываются на большой цикл. Фазовые траектории «снаружи» большого цикла наматываются на него.

Неустойчивый предельный цикл r­_1­ не соответствует, конечно, автоколебательным процессам. Он является границей, разделяющей «области притяжения» (аттракторы) устойчивого автоколебательного режима на предельном цикле r­­_­2 и устойчивого состояния равновесия в начале координат. При достаточно сильном «толчке» в системе сразу возникают автоколебания с ненулевой амплитудой.

В заключение следует сказать, что мы рассмотрели весьма небольшой математический аппарат теории колебаний и смогли при этом получить удовлетворительные примеры поведения цен, которые могут быть выражены в математической форме. В частности мы совершенно не касались случаев резонанса и рассмотрения непрерывного спектра частот.

Что касается конкретных значений для частот колебаний цены ω, то следует отметить их «фрактальность». Это означает, что любая малая часть графика цены похожа на весь остальной график. Эта особенность была замечена в начале 90-х годов прошлого века и отражает свойство фрактала – объекта, любая часть которого похожа на него самого. Например, хвойное дерево – это фрактальная форма. Оно представляет собой сеть ветвей, качественно подобных форме всего дерева, но каждая отдельная ветвь непохожа на другие. Хвойное дерево обладает глобальной структурой и локальной случайностью. В общем, мы знаем, как выглядит хвойное дерево, и можем предсказать его общую и глобальную форму с высокой степенью точности. Однако мы не знаем длину и диаметр каждой ветви.

В отношении колебаний цен фрактальность означает, что имеется «широкий спектр» частот F(ω). Возникновение спектра частот, по-видимому, обусловлено предпочтениями случайных групп экономических субъектов. Анализ этого спектра представляет собой задачу исследования.