Три маленьких вопроса
Представьте прямую, находящуюся в пространстве (не на плоскости). Представьте точку на этой прямой.
Вопрос 1: Сколько перпендикуляров можно провести к прямой через эту точку?
Запишите себе ответ на бумажку.
Вопрос 2. Сколько не перпендикуляров (т.е. под произвольными углами) к прямой можно провести через эту точку?
Ответ тоже запишите на бумажку.
Вопрос 3. Какой ответ больше – первый или второй?





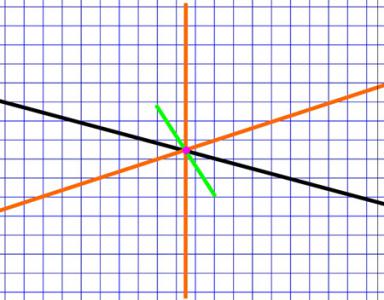
Комментарии
С утречка,шоб не расслаблялись
Охранник на входе с утра поздравил с Новым Годом, а сейчас у меня "обед" со снегопадом)))
мнооого лет назад, в сумерках, не сразу понял, почему тополиный пух прилипает к лобовому стеклу - оказалось, пух летел вместе с легким снегом. вы там держитесь.
а здесь море уже +18 - чего и вам желаю. ))
Уже вроде тает))) Завтра - лето!
Первый курс, вроде бы второй семестр. Матфака.
Я про
бесконечностиответы...Хорошо тем, кто на матфаке учился - им всё рассказали. А мне - презренному гуманитарию - как быть?
А попробуйте разъяснить, евонный и ихний - это единственной и множественное число одной и той же сущности, или принципиально разные словоформы?
Всё в мире относительно! Потому и тут надо бы относительно контекста посмотреть - ихое всехное оно, или егойное конкретно, а вы просто вежливеете?
Вы от ответа не уходите!
Народ хочет (и имеет право!) знать - что первично, смысл или придание смысла? в терминах Великой Теоремы Ауэрса...
Не помню формулировку теоремы, увы. Но наверняка она интересная и расплывчатая. Мне самой рекомендуете перечитывать Стругацких в стопицццот первый раз или датите незамутненную формулировку сразу?
Гы... пугать своей бандой это моветонное некомильфо... однако.
Это химические элементы.
Это из области
- Слушай, нахерачиться это глагол ?
- Нахерачиться, Саня, это цель !
Поверить на слово.
Там верно ответили, мощность двух этих множеств одинакова (этот раздел математики так и называется — теория множеств). Сорри, но всё же есть вещи, которые «на пальцах» трудно объяснить.
Во-первых, мощность не одинакова. Второе больше первого на подмножество совпадающее с исходной линией. И на пальцах тоже всё объяснимо: перпендикуляр это именно перпендикуляр к исходной прямой, а любой угол (второе множество) это в том числе и нулевой.
Учить вам математику, не переучить.
Вот извините, но Вы неправы.
Этим множества одинаковой мощности, как ни смешно. Математика — да, смешная наука.
Кстати, подозреваю, что и то, и это множество равно мощности континуума.
Думается что второе множество все-же больше. Оба бесконечны :). Из остатков знания помню что множество натуральных меньше множества вещественных, самое толстое - множесто всех множеств :). Перпендикуляры проводятся в 3х мерном пространстве на плоскости перпендикулярной прямой. Их мощность равна вещественному множеству. А вот мощность остальных прямых - это еще можество вещественных плоскостей. Наверно все-же это больше первого :) А так - хрен его знает, надо уже доказывать и анализировать
"Какая бесконечность больше?"
Стесняюсь, но спрашиваю - А вам зачем оно нужно? Крокодил не ловится?
Да причем тут крокодил! Не растет кокос, ема-е!
два этих континуума равномощны
У нас ТМ вроде как на третьем была. Но у нас был факультет «естественных наук».
Оба множества равномощные
Так-то оно так, но вот первое множество всего-лишь малая часть второго)))) Или нет?
Множество четных натуральных чисел равномощно множеству всех натуральных чисел. Или нет?
Точно не знаю, ибо не учили такому, но подозреваю, что равномощно. Но вопрос я ставила не в парадигме мощности множеств, а чисто количественно, так сказать)))
Оба множества бесконечные
....но бесконечны по разному:)))
А так как не сказано о каком пространстве речь (фамилии Евклид там не написано, не говоря об иных), то полагаю предполагать нужно пространство с бесконечным количеством измерений - тогда всё ещё веселей. Это в качестве субботнего.
Я вывела некие леммы, связанные с размерностью пространства и как в них можно соразмерять бесконечности - к этому пост и вела. Посмотрим, что там дальше.
На бесконечностях рулит взаимно-однозначное соответствие. Можем его для каких-то множеств ввести - они равномощные, нет - значит одна бесконечность больше другой. В примере - два множества мощности континуум, вот если бы в качестве второго было множество кривых, которые можно провести через точку, то да, такая бесконечность больше
Я тут в комментариях столько за последний час начиталась, что всяко-разно мне нужна пауза, что бы подумать)))) Пост получился очень полезным для меня.
Разных бесконечностей вообще мало - в реальной жизни нас касаются всего три варианта - счетное множество (множество натуральных чисел), континуум (множество точек на прямой), и два в степени континуум (множество всех кривых линий на плоскости), более мощные множества - это скорее абстракция уже.
Эйлер и Ньютон смотрят на вас из глубины веков недоуменно =)))
Ниоткуда они не смотрят, окститесь. Они давно разложились.
Может еще и вопросы линейности интерпретации времени добавим? +)
Нет.
Конечно, да, поскольку между ними можно установить взаимно-однозначно соответствие.
Перспективный чат детектед! Сим повелеваю - внести запись в реестр самых обсуждаемых за последние 4 часа.
Берем шар диаметром 20 мм. Проводим через его центр плоскость в пределах шара толщиной в 1 мм. Шар будет (например по объему) больше плоскости. А потом их увеличиваем до бесконечности. И они стали равны - как так?)))
Нет, предел отношения м.2 к м.1 это бесконечность. А если наоборот, то 0. Первое есть подмножество второго, => второе больше первого.
Ошибка в рассуждениях в том заключается, что вы в штуках считаете. Если считать в штуках, например в количестве точек, то отрезок будет равен лучу, луч будет равен прямой, прямая будет равна плоскости, а плоскость будет равна вселенной.
Согласитесь, оно всё же от подхода зависит. Возьмем например отрезок [0,1] и луч. С одной стороны, точек и там и там R. С другой, мера первого на прямой - 1, второго - inf.
К тому же если вселенная это хотя бы 2^R, то она будет больше плоскости.
Неверный подход даёт неверный результат. Верный подход - даёт верный результат.
Вот у вас 2 сумки яблок. В одной - мелкие, в другой - крупные. В каждой сумке одинаковое число - пусть по 10 штук. Но та, где крупные - в 2 раза тяжелее.
Ну и как сравнивать будем ? По массе или по количеству ? И то и другое сравнение - абсолютно верное.
Или вообще - по магазинной цене ? А вот там вообще мелкие яблоки могут быть в 3 раза дороже за килограмм, и более лёгкая сумка окажется в полтора раза дороже. И это тоже верное сравнение.
Совершенно верно! Потому я про прямую в посте спрашивала (количественно), а не про шар с плоскостью, т.к. и шар и плоскость толщиной в 1 мм при бесконечном расширении станут равны. Но у меня есть промежуточный вариант, где такой "фигни" не произойдет и там получается одна бесконечность больше другой, т.к. вторая - подмножество первой. а это уже говорит о том, что и математика кое в чем не менее "чудесная", чем физика.
Бесконечность - хитрая штука.
Если ее поделить пополам, то будет не пол бесконечности, а все та же исходная бесконечность...
Да, есть "дурная" бесконечность Гегеля, приводящая к Ничто,т.е. к смерти, и есть "эфирная" бесконечность Менделеева, приводящая к Все( буква йо! ), т.е. к жизни.
Страницы