Я продолжаю тему о предрассудках в современной физике.
Сегодня я собираюсь поднять вопрос о том, как формируется из фотонов изображение на экране.
Происхождение некоторых предрассудков связано с наглядной, но неудачной аналогией с взаимодействием волн на поверхности жидкости, которую Томас Юнг в начале XIX века использовал для пояснения интерференции света:

На рисунке изображены круговые волны, хотя на самом деле в опытах по интерференции свет от щелей и отверстий к экрану идет узкими лучами.
Именно с этой картинкой связан предрассудок, будто интерференционные минимумы (темные полосы на экране) появляются по причине того, что волны от разных щелей приходят в данную точку экрана в противофазе. После открытия фотонов такое объяснение стало неправдоподобным, так как гасить друг друга на экране фотоны не могут – это противоречит закону сохранения энергии.
После открытия фотонов в начале XX века физики должны были переосмыслить объяснения результатов различных опытов по интерференции, которые ранее давала волновая теория света: луч теперь должен рассматриваться не как единая волна, а как совокупность фотонов.
Однако в случае с фотонами физики удивительным образом запутались и сами себя запугали до потери способности к рациональному мышлению.
Только в последнее время теоретики начинают потихоньку осознавать, что фотон – это не элементарная частица, а неделимый на части радиоимпульс.
Если фотоны не могут друг друга гасить, то как объяснить появление интерференционных минимумов на экране, на который попадают фотоны?
Очевидный вариант: фотоны как радиоимпульсы могут при определенных условиях взаимодействовать друг с другом и менять направление движения в результате подобного взаимодействия.
При каких же условиях возможно взаимодействие между фотонами?
Если проанализировать результаты экспериментов по наблюдению интерференции света, которые физики проводят уже более трехсот лет, то можно сделать следующие выводы:
1) Длины волн фотонов должны совпадать или отличаться незначительно.
2) Направления движения фотонов должны совпадать или отличаться незначительно.
3) Плоскости поляризации фотонов не должны быть перпендикулярными друг другу.
Незначительно – это насколько?
То, что некоторые вопросы до сих пор не имеют внятного ответа, объясняется именно наличием предрассудков, передающихся из поколения в поколение.
После изобретения лазеров во второй половине XX века появилась возможность сильно упростить схемы некоторых экспериментов.
В частности, экспериментальным путем можно довольно просто оценить максимальную величину угла, при которой проявляется взаимодействие между фотонами.
В качестве примера используем классический опыт, в котором свет проходит через два узких круглых отверстия:
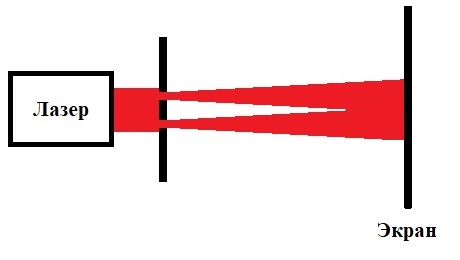
Я воспроизвел этот опыт, для чего использовал лазерный модуль R-80 с мощностью излучения 80 мВт и длиной волны 655 нм.
Диаметр отверстий в препятствии на пути лазерного луча составляет 0,6 мм, расстояние между отверстиями – 2,5 мм, расстояние от отверстий до экрана – 4 метра.
В результате на экране была получена следующая картина:
Для того, чтобы убедиться, что в данная картина является результатом взаимодействия фотонов, исходящих от разных отверстий, перекроем одно из них, например, правое.
Результат будет следующий:
Вернемся к предыдущей картинке и попробуем определить величину угла между направлениями движения фотонов по формуле для равнобедренного треугольника: расстояние между отверстиями – 2,5 мм, расстояние от этих отверстий до экрана – 4 м, значит величина угла – 0,04 градуса.
А теперь усложним схему эксперимента для того, чтобы попытаться определить максимальную величину угла между направлениями движения фотонов, при которой все еще сохраняется возможность взаимодействия между ними. Установим между отверстиями и экраном линзу, позволяющую увеличить изображение на экране:
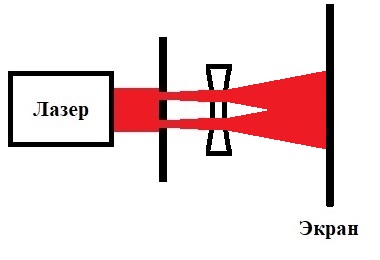
Например, при расстоянии 50 см от отверстий до линзы и 50 см от линзы до экрана можно увидеть следующую картину:
Здесь мы видим четкие интерференционные полосы только в центре.
Расстояние между отверстиями – 2,5 мм, расстояние от отверстий до линзы – 50 см, величина угла – 0,3 градуса.
Таким образом, взаимодействие между фотонами возможно, когда они движутся рядом друг с другом и расхождение между направлением их движения не превышает нескольких десятых долей градуса.





Комментарии
С таблицей умножения тоже не всё в порядке
Это вы о чем?
Двести лет копятся предрассудки в электродинамике.
Физикам просто лень разгребать эту мусорную кучу.
не надо врать. нам не лень- но мы знаем, что интеграл Френеля абсолютно точно описывает результаты наблюдения любых интерференционных картин. И я Вам уже приводил пример взаимодействия фотонов под сильно разными углами- голографические пластинки- на этих пластинках прекрасно интерферируют фотоны, прилетающие под углами в десятки градусов. То, что Вы поставили свой собственный эксперимент- это хорошо, но тот уровень обработки данных, который Вы приводите- вызывает грусть и уныние. Ваша линза не только расфокусирует (или фокусирует, наоборот) тонкие пучки света от отверстий. Она еще их и отклоняет! и угол отклонения, создаваемый этой линзой- сильно больше, чем угол расфокусировки. Так как Вы даже не озадачились вопросом измерения фокусного расстояния Вашей линзы- то и ожидать от Вас оценок углов расфокусировки и углов отклонения лучей не приходится, но для любознательных читателей расскажу- классический интеграл Френеля точно и полностью позволяет рассчитать интерференционную картину рассматриваемого эксперимента- оптические пути лучей с учетом увеличения оптического пути в стекле линзы совершенно спокойно вычисляются любым студентом третьего курса, которому читают оптику- если не на бумажке- так численно в маткаде или матлабе или на питоне.
второе- то, что у нас до сих пор есть непонятки с тем, что такое фотон и что он из себя представляет на глубинном уровне (какая там у него волновая функция, например)- не отменяет того, что корпускулярно-волновой дуализм на сегодняшний день- это самое полное и точное описание физической реальности. Да, наша макроскопическая интуиция не позволяет нам представить интерференцию одиночных фотонов- она не укладывается в голове- в нашем бытовом опыте такого нет. А эксперимент нам показывает именно интерференцию одиночных фотонов- как будто фотон один и там и тут одновременно. Мы (физики, которым лень разгребать и прочее бла-бла-бла) очень четко понимаем, что наш математический формализм позволяет очень точно рассчитывать результаты экспериментов, и что мы не понимаем, что стоит за этим математическим формализмом. Мы придумываем всякие вроде бы понятные варианты понимания- типа там волны-пилота, нелокальностей и всяких вычурных конструкций типа реальности виртуальных путей. НО! мы точно экспериментально множество раз проверили, что интеграл Френеля работает всегда и везде. В интерференции на двух отверстиях, на двух щелях, на трех щелях и на многих щелях, в пленках и каналах, в волноводах и в дифракции на круге и полуплоскости, в интерференции на решетках и на аморфных структурах, в многолучевой голографии и в лазерной интерферометрии и вообще везде, куда мы смогли дотянуться, и даже в экспериментах с одиночными фотонами интеграл Френеля работает всегда! мы также знаем, что если мы вдруг начинаем контролировать, через какое отверстие в сабжевом эксперименте проходит фотон- то интерференция исчезает. Мы не понимаем, как фотон "чувствует"- мониторим мы второе отверстие или нет, но мы знаем, что он "как-то это чувствует"- волна-пилот, кстати, предлагает кривовастенькое объяснение этого "чувствования". Однако, понимание границ нашего понимания и понимание того, где начинается наше непонимание- не отменяет того, что интеграл Френеля работает, и что волновая оптика точно описывает все наблюдаемые нами эксперименты. Че там? Кучу надо разгребать? проблема в том, что Вы даже не способны дойти до того места, откуда будет видна так куча, которую надо разгребать. А то, что Вам кажется надо разгребать- это мираж лично Вашей способности к восприятию сложной информации. отакафигня, малята.
В своей статье я рассматриваю вопрос, при каких условиях фотоны могут взаимодействовать именно между собой, а не с участием атомов вещества.
Вы говорите, что современный математический аппарат дает исчерпывающие ответы на вопросы о фотонах?
Какой размер имеет область локализации фотона в пространстве, если измерять ее в длинах волны, соответствующей этому фотону?
Какая у этой области «длина» и «толщина»?
Я подозреваю Вас в невнимательности. Я в комменте написал, что мы не знаем до сих пор волновую функцию фотона. Есть работы по расчету этих волновых функций, и есть результаты этих расчетов, но они не общепризнанные, поэтому официально волновая функция фотона, движущегося в пространстве- нам неизвестна (ну или я отстал от времени в этой теме- что, кстати, весьма не исключено). Так вот- раз не знаем волновую функцию- то и толщину, длину, ширину и объем фотона мы тоже не знаем. а вот интеграл Френеля- знаем. Мы, кстати, даже не знаем, локализован ли фотон во времени! представляет, Аспе еще в 1982м году поставил эксперименты, из которых мы, ленивые физики, вообще засомневались в том, что фотон во времени-то как-то локализован. А потом пришел Цайлингер в 1998, и еще больше заставил нас сомневаться- в его экспериментах фотон сейчас точно знал, что будет с его братом-близнецом потом, хотя это "потом" определялось случайно и потом- после уничтожения первого фотона! еще через 17 лет тот же Цайлингер, но уже с огроменной шоблой соавторов поставили еще пачку экспериментов- сильно более изысканных и сильно более надежных, чем в 98м- и опять у них фотоны летали не то в прошлое, не то будущее, не то вообще были размазаны по пространству и времени и по разным Эвереттовским вселенным сразу. А в 2022м году даже Нобелевскую премию выписали за эти квантовые парадоксы с нарушением причинно-следственных связей в жизни фотонов. Мы ваще не отдупляем, что из себя представляет фотон! Но прекрасно отдупляем, что интеграл Френеля- работает всегда и везде. И даже для этих квантовых запутанных извращений. Развлекайтесь :) фамилии я Вам привел, нагуглить смогете? Если с английским туго- то гуглите на русском про "квантовый ластик".
Господа физики, поздравляю, вы впадаете в мистицизм!
А происходит это потому, что гипотез придумано намного больше, чем экспериментов для их проверки!
Тот эксперимент, описание которого я привел в своей статье, в принципе допускает и другой вариант реализации: можно разделить луч на две части при помощи полупрозрачного зеркала и при помощи зеркал скрестить друг с другом именно лучи.
Проводился ли когда-либо такой эксперимент?
Наблюдается ли взаимодействие между лучами?
Насколько острым должен быть угол между лучами, если взаимодействие наблюдается?
Этот "эксперимент" проводится в любом волноводе и имеет численный выход в виде КСВ - коэффициенте стоячих волн.
То, что Вы пытаетесь придумывать - придумывать не нужно, ибо реализовано в куче приборов с оптическими интерферометрами, например, в прямом оптическом допплеровском гетеродине.
То, что Вы пытаетесь выдать за некое "незнание физиков" - Ваше личное незнание. Причём, Вы правы, впечатляющих масштабов.
Допустим, что два рупорных излучателя испускают направленные радиоволны на одной и той же частоте, но со сдвигом по фазе. В некоторой точке пространства эти волны пересекаются под очень острым углом (десятые доли градуса).
Будут ли волны взаимодействовать друг с другом в том смысле, что после взаимодействия направление радиолучей изменится?
Нет, конечно.
И конечно, нет - только при интенсивностях, при которых взаимодействие линейно (например, в воздухе нельзя доводить до напряжённостей пробоя в воздухе). При нелинейщине может быть всякое, тут уже нужно смотреть на конкретику.
технически, радиофотон одного пучка может краткосрочно развалиться на электронно-позитронную пару, и в этот момент эта пара может провзаимодействовать с радиофотоном второго пучка (поглотить его, например)- и тогда мы будем наблюдать именно что взаимодействие пучков фотонов. Но при энергиях радиофотонов и их плотностях потоков вероятность такого распада за время жизни вселенной пренебрежимо мала и он не наблюдается никем и никогда (одно событие за миллиард лет мы заметить не можем никак ваще). А вот на БАКе на высокоэнергетических пучках было заявление о том, что наблюдали рассеяние фотонов на фотонах- как раз в согласии с квантовой теорией и через механизм распада гамма-кванта на электронно-позитронную пару с последующим взаимодействием этой пары с другим гамма-квантом. Но это принципиально не то взаимодействие пучков фотонов, которое обсуждает kgv.
неа, никуда мы не впадаем. Мы ставим эксперименты по исследованию окружающей нас действительности, данной нам в ощущениях. И видим, что эта действительно устроена весьма нетривиальным образом. Интересным, увлекательным, но нетривиальным от слова совсем.
про Ваше предложение с разделением лучей и "проводился ли когда такой эксперимент"- я Вам в который раз повторяю- голография- узнайте, что это за слово, что оно значит, и как делаются голографические фотографии. Да, проводился. Да, проверено, что лучи, приходящие после полупрозрачного разделительного зеркала под любыми углами- от 0 до 180- интерферируют. Но не взаимодействуют. Интерферируют- это значит, что в точке пересечения этих лучей мы наблюдаем изменение пространственного распределения яркости света. Не взаимодействуют означает, что после расхождения этих лучей все их параметры остаются точно такими же, как и до пересечения, и никакого способа определить, было ли пересечение этих лучей или нет- у нас нет, то есть, свойства самих пучков после того, как они разошлись в пространстве- остаются абсолютно неизменными. А значит никакого взаимного влияния друг на друга они не оказывают.
А при малых углах (десятые и сотые доли градуса между лучами) эксперимент проводился?
интерферометр Майкельсона. Углы в минуты и секунды (углы не в десятых градуса меряют, а в минутах и секундах угловых)- интерферируют. Я Вам, как обычно, сведения из учебника физики за второй курс технического ВУЗа привожу, то есть, те данные, которые шатателю основ физики должны быть априори известны, иначе он (шататель) выглядит как бы это сказать.... бледновато.
вообще, ВУЗовский курс лабораторных по физике предполагает эксперименты по волновой оптике- наблюдение колец Ньютона, интерферометрию (определение сверхмалых перемещений, например, при изгибе толстой балки), двухщелевой эксперимент и опыты с интерференцией поляризованных пучков (для этого в лабораторных комнатах есть четвертьволновые пластинки, вращатели из всякого исландского шпата и шпинели и поляризационные фильтры разной природы). так вот этот корпус детских экспериментов закрывает вопросы интерференции на углах от нуля до 60градусов- на всем диапазоне углов! надо было просто учиться и занятия не пропускать.
Мало придумано демонстрационных экспериментов!
Ничтожно мало с учетом того, что дифракцию и интерференцию физики начали исследовать еще в XVII веке.
Не вижу я в методических указаниях по проведению лабораторных работ описания демонстрационных экспериментов, показывающих школьникам и студентам сам процесс формирования картины: «Смотрите, дети, вот так формируется дифракционная картина от одного отверстия, а вот так – интерференционная картина от двух отверстий».
Картина формируется далеко не сразу.
Диафрагма с отверстиями должна крепиться к лазеру и вместе с лазером постепенно отодвигаться от линзы. Расстояние же от линзы до экрана должно оставаться постоянным.
Я предложил свой вариант демонстрационного эксперимента и пусть кто сможет, сделает лучше.
Вы не видите указаний к проведению? А их и не надо. зачем студентам в мелких группах ставить двухщелевой эксперимент? его показывают сразу всему потоку в большой аудитории. без всяких указаний. как и эксперименты Фарадея или опыты с биением звука расстроенных камертонов.
второе- Мало демонстрационных экспериментов.... мало для чего? для Вас? ну, может быть. А вот для конкретно меня- почему-то вполне достаточно было этих экспериментов. и в аудитории, и в лаборатории. и дифракцию, и интерференцию, и голографию и интерферометрию и прецизионные измерения с помощью света я ручками потрогал, кругополяризованные пучки покрутил, интерференцию поляризованных пучков посмотрел, угол Брюстера померил и много еще чего поделал сам руками, на физ-техе Томского госуниверситета- на простенькой и сердитенькой экспериментальной базе. Поступайте на ФТФ ТГУ- Вам тоже покажут.
Будем снисходительными к автору. Всё же, согласитесь, если бы не он, то где бы нам удалось пересечься? Ну, не на профессиональных англоязычных форумах жи...
Автор не понимает, как волна может быть одновременно и... частицей... то есть, колебать только один поплавок из множества поплавков. И его можно понять. В повседневной жизни такого не случается... )
Я считаю, что фотон – не частица, а неделимый на более мелкие части радиоимпульс. Отсюда и вытекают мои вопросы о размерах области локализации этого сгустка энергии в пространстве.
Окей. Расскажите нам, что такое радиоимпульс?)
Лучше – покажу!
Рисунок из статьи
О РАЗМЕРЕ И ОБЛАСТИ ЛОКАЛИЗАЦИИ ФОТОНА
А по вертикали какая величина откладывается?)
Процитирую авторов статьи:
Это поле ПАКЕТА! волнового ПАКЕТА! читайте внимательнее и пытайтесь вникнуть в то, что там написано. Это сложно (особенно с учетом того, что авторы там местами сами себе противоречат, а местами- явную лажу выдают- когда свойства sinc например описывают- ооочень знатно налажали, прям в букваре налажали- а рецензенты пропустили... что тоже какбы намекает).
Если Вы внимательно прочитаете статью, на которую ссылаетесь, то Вы увидите, что авторы нашли решение уравнения Шредингера для волнового пакета! с разбросом частот в пакете в dk в виде sinc(dk*x)- а эта функция, внезапно- определена и ненулевая на всей числовой оси! у нее бесконечная область поддержки. А далее авторы еще и прямым текстом говорят (страница 21, первое предложение, как раз описание рис.1, который Вы скопипастили)-
это решение какого-то уравнения из какой-то волновой оптики с какими-то квантовыми уточнениями для волнового пакета для определения длины когерентности этого пакета, а не форма фотона. У них же кстати в статье на странице 20, второй абзац, сказано, что найти волновую функцию, квадрат модуля которой дает вероятность нахождения фотона в точке х- нельзя. То есть, переводя на русский- решение уравнения Шредингера для фотона найти нельзя, потому что решение уравнения Шредингера- это и есть эта волновая функция, дающая вероятность нахождения частицы в точке х. Получается, что в этой вот одной фразе авторы Вашей ссылки всю квантовую физику сразу и бесповоротно опровергли. А это не то что Нобелевская премия- это Нобелевская премия десять лет подряд. А может и просто- обычная ошибка в научной статье на русском языке в третьесортном журнале с плохим рецензированием (а Краткие сообщения по физике ФИАН в 2019м году были Q4, с 2020 едва вылезли в Q3. для тех, кто понимает).
Меня удивило в статье другое: нарисовав картинку, авторы так и не указали в выводах длину фотона в длинах волн. Это константа или нет?
Как может быть константой длина фотона?)
Длина фотона в длинах волн – постоянная или нет?
На приведенной картинке, например, длина импульса составляет десять периодов колебаний. Но почему их именно десять – непонятно. Авторы статьи нарисовали картинку кое-как?
Атом излучает фотон в течении некоторого времени. Исходя из этого, да, можно говорить о длине фотона... для данного, конкретного, случая. Но, не более того!
Например, в случае излучения атомом фотона видимого света "длина" фотона будет около 100 000 длин волны данной частоты.)
определенно нет, не 100000 длин волн. потому что для видимого света длина волны- порядка 0,5мкм- 5*10-7м. 100000 длин волн- это почти 5*10-2м= 5см. Мы абсолютно точно знаем, что фотоны преломляются в пленках толщиной в сотые доли миллиметра и даже в микроны, а значит и длина этих фотонов не может быть больше чем эти самые единицы микрон- сотые доли миллиметра. Поэтому из общих теоретических соображений следует, что если у фотона и есть какой-то размер- то он сравним по порядку величины с длиной волны этого фотона. В противном случае фотон перестает быть элементарной частицей и начинает иметь какую-то внутреннюю структуру, чего у элементарных частиц быть не может (они потому и элементарные). Дополнительная аргументация- сверхкороткие радиоимпульсы. Для частоты 3ГГц на практике удается создать сверхкороткие радиоимпульсы длиной в 0,5нс. а это- 1.5 длины волны.
Существуют ли радиоимпульсы, обладающие свойством фотонов – неделимостью на части?
То есть такой импульс либо целиком поглощается, либо целиком отражается, либо огибает препятствие, но в последних двух случаях его энергия не меняется?
Вы как-то разделяете энергию импульса и его длительность? сверхкороткий радиоимпульс- это огромная пачка фотонов, летящих рядом в очень коротком пакете. важно- это именно волновой пакет! то есть, пачка фотонов- оооочень большая, потому что энергия одного радиофотона- h*nu- настолько мала, что мы не можем задиагностировать ее доступными нам средствами и сгенерировать одиночный такой фотон тоже не можем- мы не умеем создавать такие малые порции энергии- они на много порядков меньше энергии тепловых флуктуаций электронов в проводах. поэтому мы можем сделать только мощный волновой пакет из большого числа радиофотонов. короткий во времени и пространстве, но из большого числа фотонов. И выделить из этого пакета потом одиночные фотоны, чтоб проследить их судьбу- нам технически невозможно. поэтому- радиоимпульсов, обладающих свойством фотонов- не существует. отражаются и огибают препятствия радиоимпульсы без изменения энергии отдельных фотонов, но с поглощением части этих фотонов препятствием и изменением полной энергии всего волнового пакета.
Для определения того, что из себя представляет фотон, мы использовали пробный электрический заряд. Чтобы понять суть эксперимента, возьмём листок в клеточку...
Итак, рисуем окружность радиусом в 5 клеточек. И рисуем в её центре (-) или (+). Это пробный электрический заряд. Надеюсь, с этим всё понятно?
И вот, стоило только одиночному фотону провзаимодействовать с этим зарядом, как он тут же смещался... на одну клеточку. В какую сторону? Это зависело от знака заряда и от поляризации фотона.
И вот что интересно. Каждый раз заряд смещался только на целое число клеточек! Ну, в зависимости от числа фотонов, которые провзаимодействовали с ним в данный момент времени. Какой размер у клеточки? Намного меньше диаметра протона. Примерно, в 1020 раз. Да, смело берите 20 порядков, не ошибётесь!)
врете, батенька. Поглощение фотона электроном приводит не к смещению электрона, а к изменению его импульса! то есть, к появлению у него добавочной скорости. не было никакого пробного электрического заряда. и смещение электрона не измерялось, и никакого смещения на целое число клеточек тоже не наблюдалось- и до сих пор не наблюдается, хотя поиски этих клеточек идут, но пока безуспешно. не дискредитируйте физику своими сочинениями.
Да, спасибо, дружище, за высокую оценку моего скромного вклада в наше общее дело. Однако, продолжим...
Нарисуем рядом с первым кругом ещё один. Таким образом, перед нами уже 2 пробных заряда. И на них падает фотонная волна. И если интенсивность этой волны равна 1 фотону, то придёт в движение только один из них. Если интенсивность равна 2 фотонам, тогда возможны варианты:
1. Сместятся оба заряда;
2. Сместится левый заряд, но уже на 2 клеточки;
3. Сместится правый заряд, тоже на 2 клеточки.
Аналогичные рассуждения можно провести и для интенсивности волны, равной 3 фотонам, 4 фотонам, 5 фотонам и так далее. Алгоритм, я надеюсь, вы поняли?)
Это оч. древний эксперимент, проведённый мною совместно с Аленом Аспэ ещё во время нашей совместной учёбы на факультете теор. физики в Сорбонне. У нас получилось, что в половине всех случаев смещались оба заряда. Ну, при интенсивности фотонной волны, равной двум фотонам. В чём же дело, почему 1/2, а не 1/3?
Дело в том, что если пронумеровать фотоны, то надо будет учитывать, что левый и правый пробные заряды будут смещаться и от фотона №1, и от фотона №2. Что же будет, если вместо двух фотонов интенсивность фотонной волны будет равна четырём фотонам? Давайте посчитаем...
Кароч, с ростом числа фотонов вероятность их равномерного распределения возрастает! Что уж говорить про обычную интенсивность света, измеряемую триллионами фотонов! То есть, световая волна начинает себя вести как классическая волна. Что хотелось бы ещё отметить?
Перед нами типичный пример квантовой суперпозиции! Когда амплитуды складываются, но не смешиваются! Подумайте над этим... )
А по вашему частица это такой "шарик"?
Вам вот с этим товарищем нужно познакомится
https://aftershock.news/?q=node/1342409&full&ysclid=lsk1wzbgia942694838
Особенно про "разжижающие" атом фотоны
фотон- действительно не частица. Он- КВАНТ! электромагнитного излучения. Квантовая физика говорит, что кванты- это вот такие странные объекты физической реальности, которые ведут себя одновременно в чем-то как волны, а в чем-то- как частицы. Так вот фотон- ведет себя в опытах по дифракции и интерференции как кусочек волны, а вот в опытах по фотоэффекту или по генерации лазерного излучения- как частица. Не "он есть волна и частица", а он ведет себя тут- как волна, а тут- как частица. Это как трансветсит- он ни баба, ни мужик, но если смотреть на него сверху- то выглядит как баба, а если смотреть снизу- то как мужик. так и с фотоном- ни волна и ни частица, но выглядит как и то и то одновременно.
Думаю, замоделить в "Земаксе" опыт господина kvg1967 и показать, что результат такой же.
А то у человека предрассудки, что у физиков предрассудки - тогда детерминированный цифровой болван пусть объяснит.
Для любого разумного это подсказка о том что в процессе создания полос принимают участие не только фотоны, но и какие то вторые-третьи агенты/сущности в эксперименте. Скажем среда, края материала щели и так далее...
Что подтверждается тем что те же полосы можно получить ещё кучей способов...
Таблица умножения - это частное решение распределения значений при десятиричной системе исчисления.
Фактически это не закон и не даже не теория. Это таблица частных условий предполагаемых числовых рядов.
А не является ли отверстие 0.6 мм линзой?
Нет.
На краях отверстий – дифракция.
Вот если вы замените фотоны на электроны то... получите такую же картинку просто по тому что:
С электронами тоже все непросто:
ГДЕ У ОТДЕЛЬНО ВЗЯТОГО ЭЛЕКТРОНА ВОЛНОВЫЕ СВОЙСТВА?
Для этого нужно "эти" электроны отстреливать по отдельности и регистрировать куда они "шлепаются"
Ученые уже проводили такие эксперементы и картинка та же, электроны разлетаются на экране по мin/max (нужно только найти эти работы и эксперементы)
Перечитаю позже
Для этого нужно "эти" электроны отстреливать по отдельности и регистрировать куда они "шлепаются"
Ученые уже проводили такие эксперементы и картинка та же, электроны разлетаются на экране по мin/max (нужно только найти эти работы и эксперементы)
Я перечитал и "подозрительна"...
Прямо в 1 главе, отдельные электроны всё равно оказываются там где максимумы (но в 2 и 3 все объясняют что "это не то и не так")
/Любая движущаяся частица (например, электрон) ведёт себя не только как локализованный в пространстве перемещающийся объект - корпускула, но и как волна, причём длина этой волны даётся формулой λ = h/р /
В научпопе говорят, что фуллерен о 40 атомов ведёт себя так же и чуть ли не некоторые белки. Осталось вирусы сквозь щель запустить и там уже до многоклеточных не далеко. Вот тебе квантовый мир в макромире...
Перспективный чат детектед! Сим повелеваю - внести запись в реестр самых обсуждаемых за последние 4 часа.
Автор, спасибо. Продолжайте. Я тоже считаю, что квантовая вся эта чушь (да и не только квантовая*) - это какое-то ЛГБТ в науке. Кто-то вдруг сказал, что оно правильно, и все поддержали. Хотя многим понятно, что это извращение, но молчат.
* Я до сих пор не могу осмыслить, что мы все постоянно падаем. Что у каждого своя яма есть, в которую он проваливается. Тогда направление падения у каждого своё. У каждого листочка, камешка, человека, метеорита. Но когда рисуют искажённые пространство и время вокруг массивных объектов - оно симпатично выглядит, но совсем ведь не так должно быть по их же теории. Не шар на одеяле, а всё стянуто внутрь. А у этого шара миллиарды объектов. И как всё это взаимодействует? Мне теория Ньютона и та больше нравится, хоть она основы не объясняет.
Страницы