Что делать?

Перейдём к практическим алгоритмам поиска оптимальной цены. Но сначала - о типах рынков.

Комрады в комментариях напомнили о давно читанной книге "Маркетинговые войны". А там есть одна хорошая цитата.

Самое первое, самое главное и самое важное в смысле последствий решение, которое должен принять государственный деятель и командир, это определить тип войны, в которую он погружается; здесь нельзя ошибиться, равно как и нельзя пытаться превратить войну во что-то противное ее природе.

Карл фон Клаузевиц

Самое первое, самое главное и самое важное при ценообразовании - определить тип войны рынка, на котором предстоит работать.

Используем аристотелевское членение один-несколько-много.

У нас может быть один продавец, несколько (ограниченное их количество) и много.

Рынок одного продавца называется монополией, рынок нескольких – олигополией, ну а там, где продавцов много – полиполией.

В чем различие между этими рынками? Наличие многих продавцов предполагает, что каждый участник рынка не может отслеживать действия всех вообще остальных участников. Даже если он реагирует на изменение цены нескольких своих соседей, такая реакция в общем объеме рынка будет незначительной. В результате, на рынке полиполии не будет ценовой реакции всего рынка на действия каждого отдельного участника.

Граница между рынками олигополии и полиполии будет определяться не формальным количеством участников, а степенью реакции на действия конкурентов. Даже рынок двух продавцов может рассматриваться как рынок многих продавцов, если они не устанавливают цены с оглядкой друг на друга.

Итак, с точки зрения количества продавцов, можно рассматривать такие типы рынков:

• Монополия;
• Олигополия;
• Полиполия.

Точно такое же разделение возможно и в отношении количества покупателей: может быть один покупатель, несколько и много.

Для них тоже есть термины, правда, менее известные – монопсония, олигопсония и полипсония.

Если наложить друг на друга обе эти шкалы, то получится вот такая таблица:

Покупатели	Продавцы
	Много	Несколько	Один
Много	Полиполия	Чистая олигополия	Чистая монополия
Несколько	Олигопсония	Олигономия	Ограниченная монополия
Один	Чистая монопсония	Ограниченная монопсония	Двусторонняя монополия

Для каждого рынка характерна собственная зависимость спроса от цены, и затраты, которые следует использовать в ценообразовании. Особенности всех типов рынков я рассматриваю в книге, в этой статье остановлюсь на двух - полиполии и чистой монополии. В следующей статье рассмотрю рынок чистой олигополии, когда следует принимать во внимание действия конкурента.

Как ни странно, рынки полиполии и чистой монополии схожи. Поскольку покупателей много, спрос с повышением цены постепенно (а не скачками) снижается. А поскольку роль действий конкурентов незначительна (либо конкуренты слишком мелкие, либо их нет вообще), то ею можно пренебречь. В результате конкуренция выступает как фактор внешней среды, один из многих.

Отбросим романизмъ, Клаузевица, маркетинговые войны, "справедливую цену" и прочие маркетинговые красоты. Перед нами стоит оптимизационная задача. Существует максимум некоей функции (текущей прибыли в нашем случае), можно показать, что при равномерном снижении спроса по цене такой максимум единственный. Нужно описать функцию, взять производную и приравнять нулю, как учили в школе.

Зависимость прибыли от цены можно записать следующим образом:

П = (P - Cv) * Q(P) - Cc

, где

• Q(P)- количество продаж, как функция цены,
• Сv— переменные издержки на единицу продукции;
• Сс— постоянные издержки

Взяв производную, и приравняв её нулю получаем для оптимальной цены выражение

P = Cv - Q(P) / Q'(P)

Что из этого следует? Во-первых, очевидные вещи.

Оптимальная цена никак не зависит от постоянных затрат. Это можно было видеть и из графиков, но здесь получено лишнее подтверждение.

Оптимальная цена зависит как от переменных затрат, так и от характера зависимости спроса от цены. Опять же, такой вывод был сделан из анализа традиционных методов ценообразования, здесь же он получен в явном виде.

Если нет ограничений (про ограничения я расскажу в одной из следующих статей), то оптимальная цена больше переменных затрат. Действительно, функция спроса всегда положительна. Производная, если спрос с повышением цены падает - величина отрицательная. минус на минус даёт плюс.

Во-вторых, подставляя в формулу различные математические функции спроса, можно вывести разное поведение оптимальной цены.

Так, если функция спроса гипербола, то оптимальная цена предполагает накрутку определённого процента к переменным затратам (подобно тому, как это делается в методе прямых затрат). Важное отличие - в методе прямых затрат процент рентабельности применяется ко всем товарам, либо к большим группам товаров, здесь же речь об индивидуальном проценте для каждого товара.

Если функция спроса - падающая экспонента, то наценка при оптимальной цене не относительная (в процентах к затратам), а абсолютная, в рублях. Это становится существенным при резком изменении переменных затрат. В книге я демонстрирую, что как раз такой вариант более вероятен.

Любопытные могут подставить всевозможные функции, параболу, линейную, хоть синусоиду - и посмотреть, к какому результату это приведёт.

Если мы примем какую-то математическую функцию в качестве зависимости спроса от цены, то результаты продаж по нескольким ценам (для гиперболы и падающей экспоненты - по двум ценам и более) дадут нам статистический материал для построения такой зависимости для конкретного товара.

Разумеется, лучше иметь не две, а как можно большее количество точек, для повышения достоверности результата. Ещё один момент - чем меньше разница цен, тем сильнее влияние на результат всевозможных случайных воздействий. Для того, чтобы определенная по двум точкам оптимальная цена была достоверной, разница между точками должна быть существенной. Однако, результатов любой распродажи достаточно для того, чтобы сделать предположение об оптимальной цене.

Более того, даже если товар продавался всё время по одной и той же цене, можно получить некоторый результат - ведь из-за инфляции реальная цена при этом меняется. Правда, хоть сколько-нибудь вменяемым этот результат может быть только если инфляция достаточно высока, либо если товар продаётся по этой цене очень долго.

Анализируя продажи при разных ценах можно обнаружить множество интересных обстоятельств (даже помимо самого нахождения оптимальной цены).

Однажды ко мне обратился директор сети магазинов товаров по ремонту и строительству в Поволжье с просьбой проанализировать цены на его товары. Были данные по продажам, полученные при заметном изменении цены, на распродажах и т.д. Обработка данных напрямую давала странный результат – получалось, что спрос очень слабо, а то и вообще не зависит от цены.

Но когда я разделил данные по сезонам картина прояснилась. Получалось, что осенью-зимой оптимальная наценка должна быть гораздо выше, чем весной-летом.

– Почему так получается? Что, весной и летом покупают малообеспеченные, пенсионеры? - спросил я директора сети.

– Нет, как раз наоборот, обеспеченные. Приходят профессиональные строители, которые закупают большие объёмы, но которые считают каждую копейку в цене, и которые, прежде чем купить, обследуют весь рынок, разыскивая наиболее дешёвое предложение.

– Так, значит, нужно осенью и зимой ставить большую наценку, а летом минимальную.

Директор удивился.

– Разве так можно?

А вот ещё один, свежий, пример.

Магазин торговал в течении месяца со скидками от 15 до 40%, потом по исходным ценам. Это позволило построить зависимость спроса от цены для разных товаров. Один из них (условно, Товар1) был представлен несколькими номенклатурными позициями в разных ценовых диапазонах. Привожу получившиеся графики.

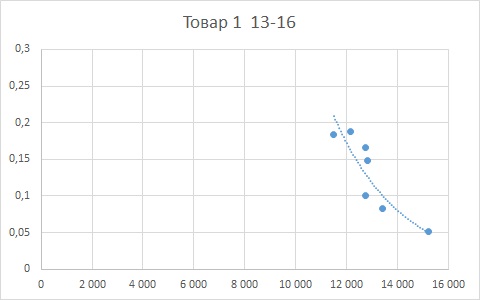
Диапазон 13-16 тысяч рублей. По расчётам, оптимальным было бы делать скидку 16,6%.

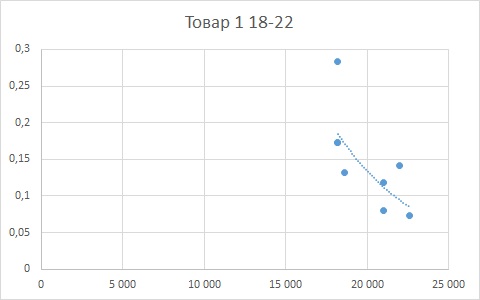
Диапазон 18-22 тысячи рублей. По расчётам, оптимальным было бы делать скидку 17,71%.

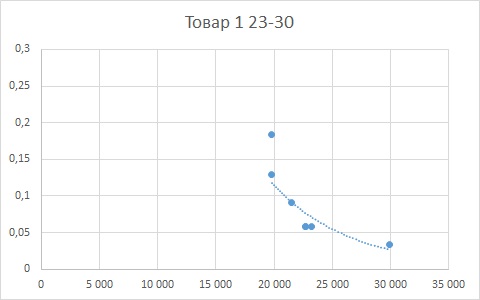
Диапазон 23-30 тысяч рублей. По расчётам, оптимальным было бы делать скидку 7,33%.

Диапазон 31-36 тысяч рублей. Спрос практически не зависит от цены.

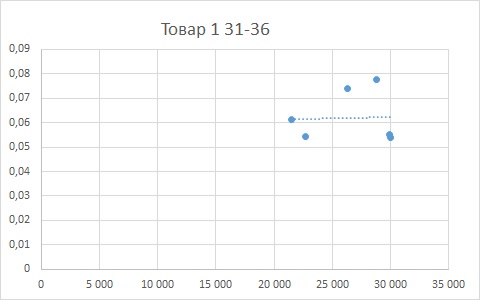
Даже визуально видно, что с переходом в более высокий ценовой диапазон зависимость спроса от цены снижается. Более состоятельные покупатели  меньше обращают внимание на скидки, а больше на качество. И для диапазона 31-36 есть смысл делать не скидку, а наценку (в разумных пределах, конечно).

Может быть, такие выводы можно было бы сделать, сегментировав потребителей, выяснив их предпочтения, готовность к покупкам, проведя анкетирование и т.д. Но по итогам продаж это и так видно, без сложных исследований. А главное - результаты получаются, и постоянно уточняются оперативно, в ходе продаж, причём с увеличением статистики постоянно повышается достоверность результатов.

Приглашаю вас на свой канал, посвящённый ценообразованию.