Камрады ! Нужна ваша помощь.
Эта нерешённая задачка не даёт мне покоя, поскольку время от времени всплывает в памяти. Проработав 18 лет в Хьюстоне, в рамках Программы МИР-Шатл, а потом и Международной Космческой Станции, я неоднократно предлагал решить её американцам, инженерам НАСА. Безуспешно... Хотя, что с них взять - НИ ОДИН из них не смог ответить мне на простой вопрос насчёт их (нелепой) шкалы температур Фарентгейта: Какое природное явления в этой шкале взято за "0" и какое - за "100" ?. Приводил им в пример шкалу Цельсия - что там взято за 0 и что за 100 Невероятно, но никто из них (сходу, без Педивикии) не знал ответа на вопрос о шкале Фарентгейта. И это - сотрудники НАСА. Хотя, что с них взять - 2/3 из них не знает имя человека, полетевшего в космос первым.
Отработал я, значица, на НАСУ, вышел на пенсию, переехал во ХлорИду.
Все свои пенсионные накопления за 18 лет вбухал на первый взнос, чтобы купить дом (в рассрочку на 25 лет.)
И живу я теперь, в получасе езды от космодрома, что на мысе Канаверал.
Моим соседом оказался бывший учитель математики. Предложил ему эту задачку.
Задачу эту он решить тоже не смог. Кстати, замечательный человек, большая умница, с прекрасным чуством юмора.
Надо заметить, что в омеричке, хорошие соседи - это большая редкость. В основном - стукач на стукаче.
К этому их приучают со школы. В том числе и стучать на своих родителей.
Поэтому стукачество - у американцев в крови "с младых ногтей".
Сразу вспомнил примечательный случай по этой части. Насчёт стукачества.
Дело было в Хьюстоне, в период работы по Программе "МИР-Шаттл".
По работе познакомился я с французским астронавтом/космонавтом Жаном Лу Кретьеном.
В своё время Жан Лу дважды летал в космос на советском Союзе Т-6 (1982 г.) и Союзе ТМ-7 (1988 г.) и даже проходил подготовку к полётам на космическом корабле «Буран» (1990-1993 г.г.) А в начале 1997 г., когда я с ним пересёкся по работе, Жан Лу проходил в Хьюстоне подготовку для полёта на Шаттле ( STS-86). На время пребывания в Хьюстоне он с женой сняли дом, недалеко от Космического центра им. Джонсона (JSC). Надо отметить, что Жан Лу неплохо владеет руским языком.
Сказывается длительное пребывание в СССР, жена у него, кстати - русская.
Поэтому он унаследовал много руских привычек (в том числе и употребление водки).
И вот Жан Лу рассказывает, что заехав в дом он, как водится на новоселье, устроил небольшую вечеринку для людей, живущих в домах, непосредственно граничаших с его домом, чтобы познакомится. С одним из этих соседей они подружились (типа) и тот стал по вечерам частенько заходить к гостепреимному Жан Лу, потрындеть и выпить водочки (как я уже упоминал - привычка которую Жан приобрёл в СССР) ... И вот однажды, этот сосед, заметив, что трава на заднем дворе у Жана намного выше нормы, пишет об этом донос в Home Owner Assosiation (типа Правления ЖСК в СССР). Те, (проверив сигнал) выписывают Жану штраф в $100 за нарушение правил "ЖСК".
И вот Жан Лу рассказывает мне (на неплохом русском языке):
"Можешь себе педставить, этот 3,14дор (сосед), опять, как ни в чём ни бывало, приходит ко мне вечером, пить мою водку !"...
Пардон - отвлёкся. Нахлынули воспоминания...
А что ещё делать, как не педаваться воспоминаниям... когда ты на пенсии,
В догонку - о стукачестве на работе. Вот уж где оно процветает ! Вот уж где надо держать язык за зубами.
Стоит сказать что нибдь такое этакое (о работе, о политике) - через полчаса об этом становится известно начальству.
Со всеми вытекающими...
Возвращаюсь к основной истории с задачкой:
Дело было в 10 классе. Учился я тогда в 38-й средней школе.
Это та, что была около Тучкова моста, на Васильевском острове в Ленинграде.
Теперь там её уже нет, с начала 90-х там громадный пизнисс центр (месторасположение уж больно "фартовое")
И вот однажды, к нам в класс входит незнакомый нам мужичок и говорит нам:
"Я ваш новый учитель по математике.
Моя фамилия - Пузыня...
Даю три минуты на смех, после чего выгоняю из класса !"
Имени/отчества этого Пузыни я уже не помню (он замещал нашу математичку примерно месяц)
Но нам он понравился. Очень классный преподаватель. Через несколько дней, под конец урока, он подкинул нам интересную задачку, которую надо было решить чисто геометрическими методом. Никакой, панимаш, там - тригонометрии:
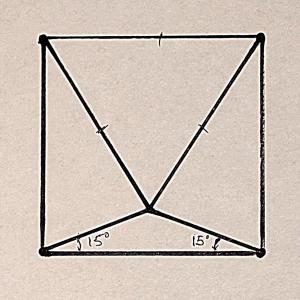
Имеется квадрат. Из нижних его углов, под углом в 15 градусов роводятся две прамых линии до их пересечения.
Точка пересечения соединяется с двумя верхними углами квадрата.
Доказать (чисто геометрическими методами), что получившийся треугольник является равносторонним.





Комментарии
Задачу решать не буду, а зарисовки давайте! :)
Жанровые зарисовки из американЬской жизни находятся в тексте статьи.
Про соседей и про повальное стукачество (со школьной скамьи)
Странно, что Вы их не заметилои
Заметил, давайте ещё...
По изначальному предложению ноль по шкале Фаренгейта определялся по самоподдерживающейся температуре смеси воды, льда и хлорида аммония (соответствует примерно −17,8 °C), а +96 °F — температуре тела здорового человека
То есть идея была в том, чтобы уличные температуры там, где жил сам Фаренгейт, были только положительные и меньше 100
А из каких соображений был взят именно хлорид аммония? Всяческих смесей придумать можно много у которых интересные свойства есть. Кстати, за 100 была принята температура здорового человека, просто слегка ошиблись.
Видимо в аптеках тогда свободно продавался.
Вытирайте пыль с бритвы Окаямы чаще.
Равновесную смесь воды со льдом даже без аптеки получить можно, поэтому - убери от меня бритву, гад...
Это не моя....
Что касается квадрата- втыкаем ногу циркуля в две верхние точки и засечки от радиусов дуг сойдутся в центральной точке.
Что касается температуры 100 град по Фаренгейту, то это температура тела его жены.
(Ответы настолько просты, что кажется что они должны быть неправильными.)
Здоровая была видать жена, щитовидка хорошо работала.
можно без зарисовок Высота треугольника h = b/2*tg(a), где h высота b основание а - угол.
Предположим, что треугольник равносторонний с углом 60 градусов, Второй треугольник равнобедренный с углом 15 градусов, Тогда b -сторона квадрата и основание обоих треугольников, а высота обоих треугольников в сумме тоже должна быть равна b.
Считаем b/2(tg(60)+tg(15))=h1+h2= b/2*2 = b.
Все доказано.
А чего тут доказывать?
Признак подобия, по двум сторонам и углу между ними
Помедленеее пжалуста !
А зззаписываю ...
Аналитического решения без тригонометрии нет.
Потому как можно составить 3 уравнения с 4-я неизвестными углами:
1 - Сумма углов верхнего треугольника равна 180
2 - Сумма верхнего угла левого треугольника и левого угла верхнего треугольника равна 90
3 - Сумма 2-х неизвестных углов левого треугольника равна 105
Дел
Ну, и ... ?
Представим решение задачи, или щёки от величия надувать будем ?!
Мне же самому интересно узнать решение этой задачи.
Поэтому я и представил её тут.
А ниччо что там примерно 30 градусов углы обозначены как 15 градусов?
А ниччо, что там нет равнобедренного треугольника, если его мерять чисто геометрическими методами?
Сторона тругольника равна стороне квадрата. Вписывается в окружнсть. Дальше считаем углы 15 - 75 -90. И получаем внутренние углытреугольника по 60 градусов.
Для начала с чего бы вдруг строна треугольника равна стороне квадрата?
Задачку нужно решить, а не проверить решение.
(на картинке опечатка, надо (180-30)/2= 75 градусов)
Все правильно. Но ТС просил решить задачу в прямом направлении.
есть разные методы решения задач и доказательств теорем. Например, доказательство от противного. Предположем что этот треугольник не такой, парам-парам вышла ерунда, значит теорема верна. Я сделал построения, получил чертёж как в условии задачи. Задача доказана.
Из условия задачи, у тебя:
1. только два нижних угла нижнего треугольника (третий угол вычисляется);
2. внешний контур - квадрат;
3. точка пересечения прямых.
Все. Из этого надо получить соотношение сторон верхнего треугольника, и получив в результате то, что они одинаковые --> сказать: "да треугольник равносторонний".
Или равенство всех его углов
Ответ у доски (выполняется поверх чертежа в условии задачи):
1. Проведём дополнительные построения, возмём циркуль и получим точку С.
2. Посчитаем углы и получим угол CBF равный 15 градусов
3. Угол 15 градусов удовлетворяет условиям задачи. Задача доказана.
Поэтому выше написал: Аналитически без тригонометрии не решается.
А нам не надо аналитически. Посмотрите условия задачи.
"Доказать (чисто геометрическими методами), что получившийся треугольник является равносторонним."
Правильно. Геометрическим методом, но не графическим методом.
Правильное решение, ошибок не вижу. Если верно это решение, то обратное решение тоже верно!
А вы уверены что нет других вариантов нарисования этих треугольников, дающих 15 градусов?
В квадрате и с описанным вариантом? Да, уверен. Во всех квадратах ьакие треугольники будут пожобны а значит углы будут равны.
Вот нарисуйте не исходя из заранее принятия равносторонности - и посмотрим ))
Решение от обратного, на первой странице комментов с чертежем.
Прямое решение -- хз.
От обратного это не решение. Это как бы вы подставили в квадратное уравнение один из корней, убедились что он подходит и сказали, я его решил, проигнорировав существование второго корня. А тут может бесконечное множество решений? И равносторонний треугольник всего-лишь одно из них? Вот поэтому задачу нужно решать а не проверкой заниматься. И доказательство от противного должно звучать по иному - допустим что не существует единственного решения, которым является равносторонний треугольник.... и тд
Это Евклидова геометрия. А то что вы написали совсем из другой сферы знаний.
Стоит один раз доказать что если углы по 15 то треугольник равносторонний и все, иных вариантов нет. Не понимаю на каком основании вы эту чушь пишите:
И решение от отбратного это однозначно решение, и оно геометрическое.
Может и есть прямое решение, но мне лично лень тратить полдня-день на это.
Доказательства нет у вас а ерунду пишу я? Оригинально)))
Еще раз для тупых, как минимум тупых в геометрии. Решение приведено выше. Оно геометрическое и верное. Если оно не верно -- опровергните, геометрическими верными утверждениями, а не "а может тут возможно целое множество углов"...
Доказываю. Существует бесконечное множество равносторонних треугольников, не удовлетворяющих условиям задачи.
Для тупых
Ага. Существует. Где-то там, вне этого квадрата, либо с углами не 15 град. Если угол 15 град, то только такие треугольники как на чертеже.
Тебя по геометрии не атестовали видать, ибо знаний на уровне азов ноль. Ты вообще Евклидову геометрию не понимаешь.
Окружность это кривая равноудалённая от центра. Две окружности начерченные из углов квадрата пересекаются в единственной точке С (в поле квадрата). Это аксиома, она не требует доказателства.
Через две точки можно провести только одну прямую. Эго аксиома с которой начинается изучение геометрии. Через точки В и С можно провести единственную прямую и угол у неё будет 15 градусов. 15 градусов в геометрии всегда равны друг другу, это не градусы Цельсия и Фаренгейта!
Поэтому задача решена и доказана.
Подгон ответа под вопрос
Эээ.... считаются углы у боковых треугольничков, выясняется, что они равнобедренные.
Извиняюсь, если кому-то проспойлил....
И как выяснить, что они равнобедренные?
углы одинаковые
докажите, что одинаковые.
Одесса чья?
Задача оказывается легко и просто через углы...
Во во, столько народу об эту задачу зубы обламало а тут - "да нехрен делать!"
Это слова.
Приведите подробное докозательство со всеми геометрическими построениями, пожалуйста
Я не знаю что у вас там за народ её решал, скорее просто видимо им было лень. Но действительно, через углы решается она просто мгновенно. Надо просто заметить равенство двух боковых треугольников и записать всё суммы углов которые получаются при пересечениях внутри квадрата, а так же вытекают из сумм углов получившихся треугольников.
Страницы