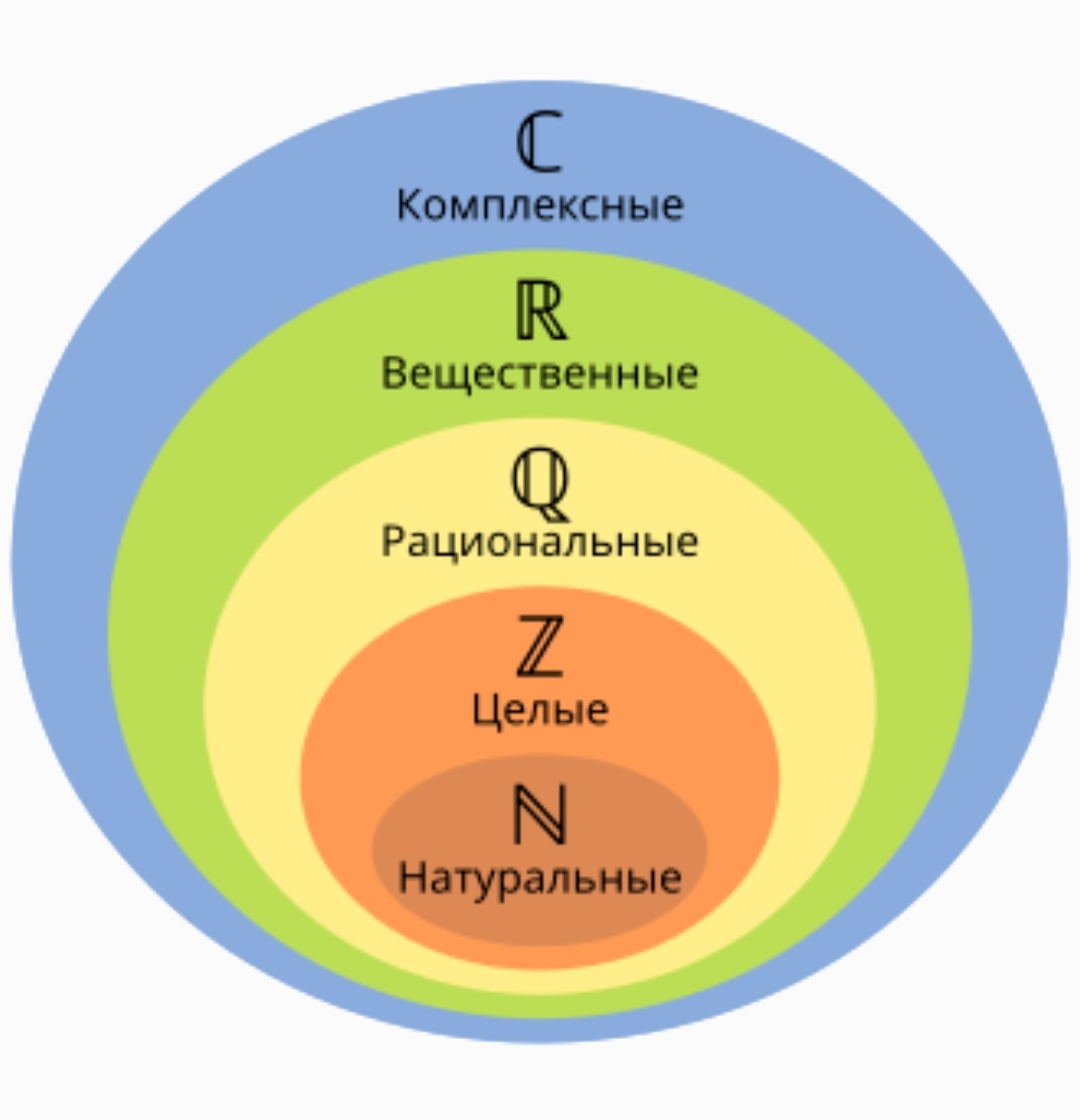
Вы когда-нибудь слышали о мнимых, или как ещё говорят, комплексных числах? Они — бедные родственники в программе математического образования. Действительно, очень часто для школы их считают слишком сложными, а для университета — слишком простыми. То есть в школе вам о них не факт, что расскажут, а когда вы придёте в универ, вам скажут: «Ну как вы знаете, это комплексные числа».
Комплексное число или мнимое — это число, которое не имеет аналогов в нашем реальном вещественном мире. Например, квадратный корень из минус единицы. Действительные числа мы с вами наблюдаем каждый день, например, π, золотое сечение или просто количество людей в очереди за булочками. И, несмотря на свою такую нереальность, они очень важны для науки. Так, например, они лежат в основе одной из главных физических теорий. Какой именно, спросите вы? Расскажем в конце.
Как и зачем учёным пришлось извлекать квадратные корни из отрицательных чисел.
Всем привет! Поехали! История мнимых чисел берёт своё начало аж в 1494 году. Именно в этом году Лука Пачоли*, более известный как учитель математики Леонардо да Винчи*, публикует книгу «Сумма арифметики, геометрии, пропорции и пропорциональности» — полный сборник всех математических сведений, которые были известны во времена Ренессанса в Италии. В этой книге есть часть, посвящённая кубическим уравнениям.
ax3+bx2+cx+d=0
Люди пытались решить это уравнение более 4000 лет: греки, вавилоняне, персы, египтяне, арабы — все предпринимали попытки его решить, но так и не достигли результата. Именно поэтому Пачоли пришёл к выводу, что не существует формул, с помощью которых можно было бы находить корни кубического уравнения. Для нас это может прозвучать странно, потому что если мы, например, уберём ax3, то мы получим обычное квадратное уравнение, которое мы научились решать ещё в восьмом классе.
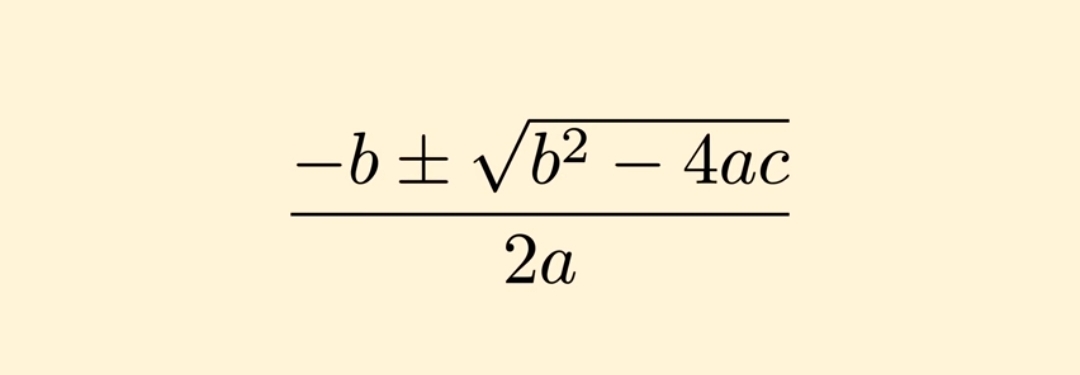
В школе нас часто учат только формулам, зачастую готовым, совершенно забывая тот факт, что в древние времена математики использовали для решения уравнений геометрические фигуры. В те времена на самом деле не было математических символов, то есть переменную не обозначали за букву «X», всё описывали с помощью фигур и слов.
Для примера возьмём уравнение:
x2 + 26x = 27
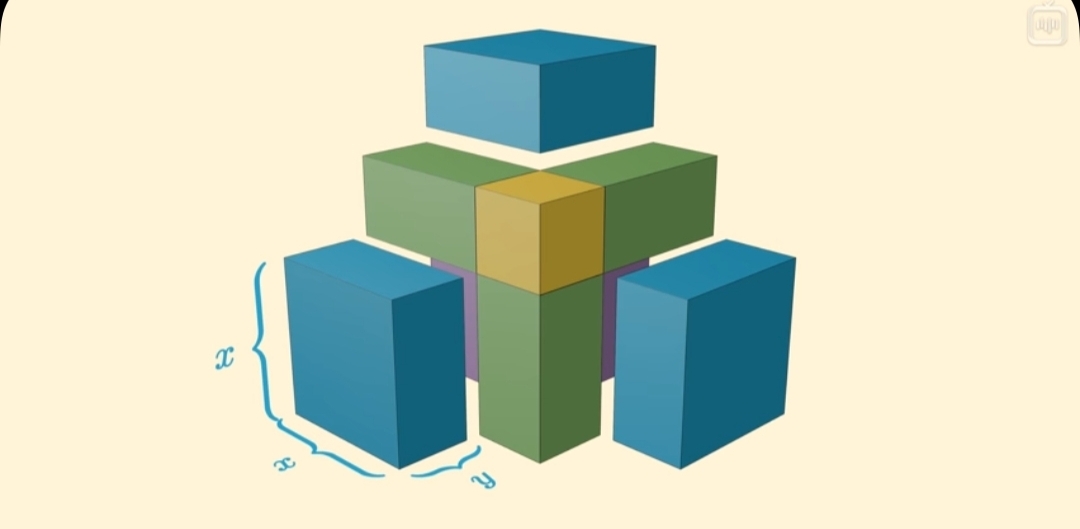
Древние математики представляли бы себе реальный квадрат со стороной «X», а под «26x» они понимали бы прямоугольник с шириной, равной 26, и высотой, равной «X». И согласно уравнению сумма этих площадей равна 27.

Мы можем взять прямоугольник с площадью «26x» и разрезать его пополам. Теперь у нас есть два одинаковых прямоугольника с площадью «13x».

Мы можем расположить все фигуры так, чтобы у нас получился практический квадрат, для которого не хватает вот этой ещё одной части.

Но мы знаем, что недостающая часть — это квадрат со стороной 13. Так как я добавляю квадрат с площадью 132, то мне нужно прибавить 169 к обеим частям уравнения, чтобы баланс во Вселенной не нарушился.

Теперь у нас есть квадрат с площадью 196. Корень из 196 равен 14, а это значит, что сторона квадрата – 14 и «Х=1».

Это прекрасный и очень наглядный способ решать квадратные уравнения, но, к сожалению, он не является полным. Мы с вами знаем, что квадратные уравнения всегда имеют два корня. Первый из них мы уже нашли — это «Х=1», а вот второй корень... Ну, если вы, например, сами решите это уравнение с помощью дискриминанта, вы найдёте, что он будет равняться «-27».
Согласитесь, с помощью одной лишь геометрии длин площадей объёмов отрицательные числа ну никак не получить. Что сделали древние? Всё очень просто — гениальный выход! Они на протяжении нескольких тысяч лет просто игнорировали существование отрицательных чисел. Наверное, они были немножко физиками и могли сказать: «не физично». Поэтому для самых первых математиков, чистых и прикладных, отрицательные числа попросту не существовали. А значит, и не существовал общий вид квадратных уравнений, потому что из общего вида то получались бы отрицательные корни, которые не существуют, которых нет, просто нет.
Зато вместо него было шесть версий квадратного уравнения. Они были составлены так, чтобы коэффициенты в них всегда были положительными.
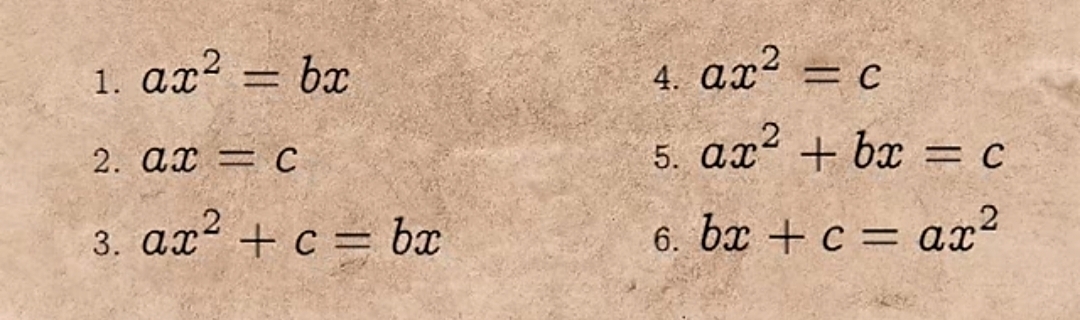
Помимо квадратных уравнений учёные пробовали иметь дело и с кубическими.
Чем ниже человек душой,
тем выше задирает нос.
Он носом тянется туда,
куда душою не дорос.
Вот такие персидские частушки. Причём здесь стихи, подумали вы? Всё дело в том, что их автор, Амар Хаям, был ещё и математиком. Собственно, в XI веке именно он вывел 19 видов кубических уравнений, в которых коэффициенты всё так же всегда были положительными.
Помним, отрицательных чисел у нас не существует. Некоторые из них он всё-таки смог решить с помощью кривых второго порядка — гиперболы и окружности, но своей цели нахождения общего решения кубического уравнения он тоже не смог достичь.
Через 400 лет, и за 4000 километров решение этой проблемы постепенно начало формироваться. В 1510 году в Италии математик Сципион дель Ферро** находит надёжный способ, с помощью которого можно решить неполное кубическое уравнение — это уравнение, в котором отсутствует квадратный член и.. никому ничего не говорит. Почему?
Оказывается, что если учитывать исторический контекст, то его поведение очень легко можно объяснить. В те времена быть математиком было очень тяжёлой работой. Если вы получали какой-нибудь результат, то другие математики могли прийти к вам и бросить вам вызов. Интересно, били ли они друг друга своими математическими заметками по лицу?
Математические дуэли
В те времена были распространены математические дуэли. Если какой-то математик не нравился вам, например, как личность, или наступил вам на ногу, когда вы спускались со своей кареты, то вы смело могли, так сказать, бросить ему вызов и отомстить обидчику интеллектуально.
Эти математические дуэли — это было такое мероприятие, где встречалось два математика, и они обменивались списком задач. Кто решил большее число задач из этого списка, собственно, тот и был победителем, а второй был проигравшим и с позором уходил, потому что проводились эти дуэли на глазах у многочисленной публики. Причём среди этой публики были не только математики и учёные, а очень даже именитые люди.
В те далёкие времена, да, в отличие от нынешних, для людей было нормально даже если ты не математик, не биолог или не химик, интересоваться точными естественными науками для того, чтобы быть всесторонне образованным и развитым. Собственно, почему я это говорю? Потому что теоремы и труды математические, которые мы сейчас знаем, были выполнены не профессиональными математиками, то есть людьми, у которых профильное образование было совершенно иным.
Например, тот же самый Ферма был юристом, а все свои утверждения, которые, так сказать, он сформулировал, теоремы, и та же самая великая теорема Ферма — это просто были его заметки на полях книги по математике, которую он читал, а на жизнь он зарабатывал юриспруденцией.
Вот часто ли вы видели юриста в нынешнее время, который на полях книги формулирует теоремы, причём такие, что их потом по 300 лет не могут доказать? Собственно, наш дель Ферро был не прочь поучаствовать в таких математических дуэлях и, зная, что никто в мире не может решить неполное кубическое уравнение, он держит своё решение в секрете, чтобы на случай дуэли он мог эту задачу дать противнику и быть уверенным, что он её точно не решит.
Лишь в 1526 году, уже будучи на смертном одре, он открывает секрет своему ученику Антонио Фиору**. Фиор не был таким же талантливым, как дель Ферро, но он был молодым и амбициозным. После смерти дель Ферро 12 февраля 1535 года Фиор бросает вызов математику Никола Фонтана Тарталья**, который недавно переехал на родину Фиора в Венецию.
Никола Фонтана всю жизнь знал, что его зовут Никола Тарталья, но что он фонтан, точно не знал. Когда он был ребёнком, его ранил французский солдат, что сделало его заикой. Именно поэтому его и называли Тарталья, что на итальянском означает «заика».
Тарталья рос в бедности, поэтому, как и многие математики того времени, он был самоучкой. Его путь становления математиком был полон препятствий, и сейчас его, пусть даже невысокое положение, находится под угрозой. Ему брошен вызов молодым Фиором. По традиции Фиор предложил Тарталье 30 задач.
Мы с вами помним, что Фиор умел решать неполные кубические уравнения и считал, что никто больше в мире решить их не сможет. Собственно, поэтому каждое из этих тринадцати заданий было связано с необходимостью решить неполное кубическое уравнение.
Сейчас важно уточнить одно правило математических дуэлей: тогда вы могли дать своему противнику только те задачи, которые сами могли решить. Ну иначе какая это дуэль? Если вы просто перекинете списком нерешаемых задач, это не выявит победителя.
Собственно, поэтому Тарталья практически до конца срока испытаний не приступал к решению этих задач. Он считал, что сам Фиор не может их решить и хотел его в этом изобличить. Но тут до Тартальи доходят слухи о том, что у Фиора есть решение. Он умеет их решать. И, по легенде, ночью, до того как нужно уже было предъявлять свои решения, Тарталья садится решать кубическое уравнение, и магия! Он справляется! У него получается решить кубическое уравнение, но находит он решение не неполного кубического уравнения, а кубического уравнения в общем виде.
Это был тот самый момент истины, потому что древние греки умели решать квадратные уравнения, а вот с кубическими не справились даже арабы, которые на тот момент считались чуть ли не королями арифметики.
Наступает день X, Тарталья и Фиор встречаются и на глазах у большой толпы обмениваются решениями. Тарталья, так сказать, открыв уже свой новый метод, решает все 30 уравнений Фиора. А вот Фиор не смог решить ни одной задачи, которую предложил ему Тарталья, хотя и владел формулами дель Ферро. В общем, излишняя самоуверенность Фиора ни до чего хорошего не довела.
Так как же Тарталья смог решить задачу, которую не могли решить на протяжении тысячелетий? Чтобы сделать это, он по сути расширил метод, который мы с вами уже до этого обсуждали. Только мы использовали квадраты, а он использовал кубы.
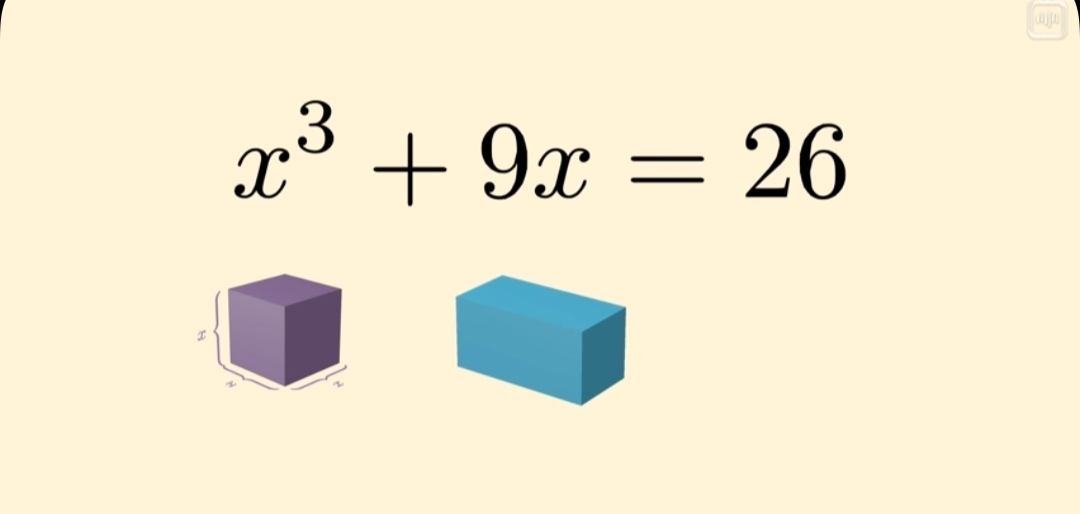
Мы не будем вдаваться в технические аспекты его решения, лишь отметим главную идею: с помощью перестановки различных кубов и параллелепипедов, ну и небольших вспомогательных арифметических действий, Тарталья пришёл к выводу, что неполное кубическое уравнение можно свести к квадратному, которое на тот момент легко уже могли решить.
Таким образом, Тарталья становится вторым человеком в истории, который смог решать неполные кубические уравнения, и его гениальность заключалась в том, что для того, чтобы не пользоваться каждый раз геометрией, не рисовать эти кубы, он свой метод, так сказать, преобразовывает в алгоритм.
По сути, он создаёт формулу, с помощью которой можно вычислять корни. Но вот что самое интересное: он записывает свой алгоритм не с помощью формул, как это мы делаем сейчас, а в форме стихотворения.

Необычно, не правда ли? Вот попробуйте, например, алгоритм решения квадратного уравнения записать в стихах. Если у вас получится, мы обязательно его опубликуем за вашим, конечно, авторством во всех социальных сетях. Дерзайте, а мы возвращаемся к истории.
Победа делает Тарталью своего рода знаменитостью. Все хотят узнать, как же он нашёл решение неполного кубического уравнения. Особенно сильно в этом был заинтересован Джероламо Кардано***, учёный, живший в Милане.
Как вы уже можете догадаться, Тарталья отказывается раскрыть свой секрет Кардано. Но Кардано был весьма настойчив. Он писал Тарталье письма: то с угрозами, то с лестью, то с просьбами — что он ему только не писал. Но, по итогу, рыбка попалась на крючок. Кардано удалось заманить Тарталью в Милан с помощью денег.
Именно там, 25 марта 1539 года, Тарталья раскрывает свой секрет Кардано, но лишь после того, как тот поклялся, что никому не расскажет его метод и никогда его не опубликует. Кардано был очень рад своим новообретённым знаниям и пользовался ими в качестве развлечений. Ну вот такое хобби было у человека — решать кубические уравнения. А какое у вас? Но, несмотря на это, у него была более возвышенная цель. Он хотел найти решение полного кубического уравнения, и он его находит. А именно, он находит метод, с помощью которого полное кубическое уравнение можно было бы свести к неполному, которое затем можно было бы решить с помощью метода Тартальи.
Несмотря на то что по факту именно Кардано научился решать полные кубические уравнения, я позволил себе до этого сказать, что их научился решать Тарталья. Всё-таки отдадим ему должное, что Кардано научился сводить кубические уравнения произвольного вида к неполным, которые всё-таки Тарталья научился решать самостоятельно. А Кардано, по сути...
Слушайте, знаете, мне пришла интересная аналогия: Тарталья — он как чистый математик, он что-то открыл, доказал. А вот Кардано — он как прикладной математик, он прикрутил. Собственно, это так и было.
Кардано очень обрадовался. Ну согласитесь, было бы странно, если бы он не обрадовался, что смог решить задачу, которая была неподвластна самым лучшим умам человечества на протяжении тысячи лет. Ну и, конечно же, он хочет опубликовать свою работу. Единственное, что его сдерживает — это клятва, данная Тарталье. Ну, собственно, можно было бы подумать, что на этом всё и закончилось, но, как мы знаем, мы сегодня умеем решать кубические уравнения. Почему? А всё потому, что в 1542 году Кардано отправляется в Болонью и встречает там математика, который оказывается зятем уже известного нам Сципиона дель Ферро, который когда-то и раскрыл метод решения неполного кубического уравнения своему ученику Антонио Фиору.
Кардано находит этот метод решения неполных кубических уравнений в старых записных книжках дель Ферро. Оно опередило решение Тартальи на несколько десятилетий, и теперь, по мнению Кардано, он может опубликовать заметки дель Ферро, тем самым не нарушая клятву, данную Тарталье.
(Решил задачу трёх тел.. 😹)
Спустя 3 года Кардано публикует книгу «Арс магна» — обновлённый сборник всей известной математики на тот момент. Интересно, что название книги «Арс магна» с латинского переводится как «высокое искусство». Вот как тогда относились к математике!
Несмотря на то что Кардано признаёт вклад Тартальи, дель Ферро, Тарталья всё равно остаётся недовольным, и он пишет оскорбительные письма в адрес Кардано. И отчасти Тарталья был прав, ведь общее решение кубического уравнения до сих пор называют формулой Кардано.
«Арс магна» — это было феноменальное достижение математики на тот момент, ведь с появлением этой книги происходит некоторая математическая революция. Если до этого превалировала геометрия создана, ну или открыта, да, более корректно, греками, то в этот момент у нас геометрия отходит на второй план, и на первый план выходят символы алгебры.
В процессе написания «Арс магна» Кардано приходит к выводу, что существуют такие кубические уравнения, которые нельзя решить с помощью известного ему метода. Например,
x3 = 15x + 4
Что же с ним не так? Оказывается, что если это уравнение решать по методу Кардано или Тартальи, то появляются корни из отрицательных чисел.
В те времена к самим отрицательным числам относились так себе, а тут надо ещё из них корни извлекать. Представляете шок публики того времени?
Кардано спрашивает Тарталью, что с этим делать, но Тарталья намекает ему, что Кардано недостаточно умный для того, чтобы пользоваться даже своей формулой. Помним, что Тарталья был обижен на Кардано. Он попросту тоже не знал, что с этим делать. Чтобы решить это уравнение, Кардано возвращается обратно к геометрии и пробует метод с кубами, который приводит его к квадратному уравнению.
Это квадратное уравнение создаёт геометрический парадокс. Кардано находит часть квадрата, которая должна иметь площадь равную 30, а стороны равны пяти. Мы легко можем найти площадь всего квадрата 5 * 5 = 25.

Таким образом, чтобы числа сходились, Кардано каким-то образом должен добавить отрицательную площадь.
Во́т откуда происходит концепция корня из отрицательного числа! Чисто из геометрических соображений должна была появиться отрицательная площадь.
Честно говоря, несмотря на то что до записи этого видео я знал некоторые аспекты истории развития комплексных чисел, но вот как это было связано с квадратами и кубами, я знал не в полной мере. И поэтому при записи данного видео мне самому, как математику, было крайне интересно посмотреть на историю развития. Ставьте лайк, если вам тоже! Оценим, так сказать, совместную работу всей команды Лаплас, нам будет приятно.
Но оказывается, что это не первый раз, когда появлялся корень из отрицательного числа в математике. На самом деле, ещё в книге «Арс магна» возникает такая задача: нужно найти два числа, которые при сложении равны 10, а при умножении дают 40.
x + y = 10
xy = 40
Из этих двух уравнений можно сделать квадратное уравнение:
y = 10 - x
x (10 - x) = 40
x2 + 40 = 10x
Если решать это квадратное уравнение, то как раз-таки и появляется корень из отрицательного числа.
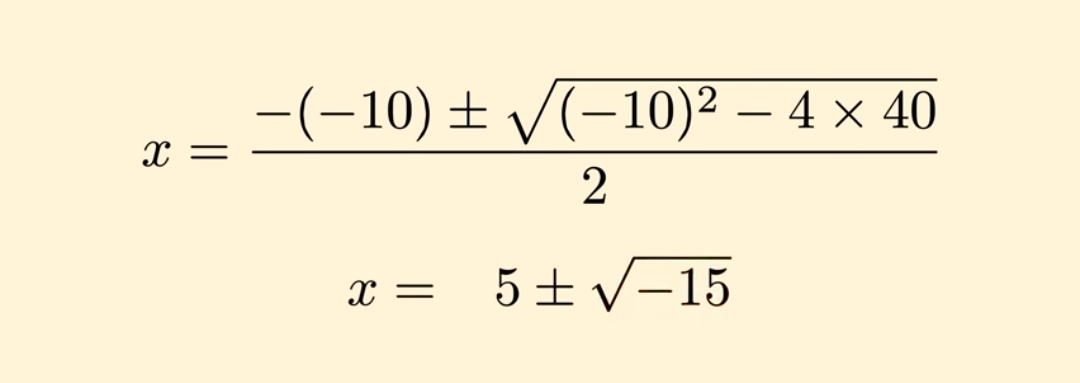
Поэтому математики того времени делают очевидный вывод: решения у этого квадратного уравнения не существует. Вот и всё, потому что тогда математики считали, что корень из отрицательного числа — это признак отсутствия решения у уравнения.
Но это кубическое уравнение имело одно отличие. При переборе значений можно увидеть, что существует решение: X = 4.
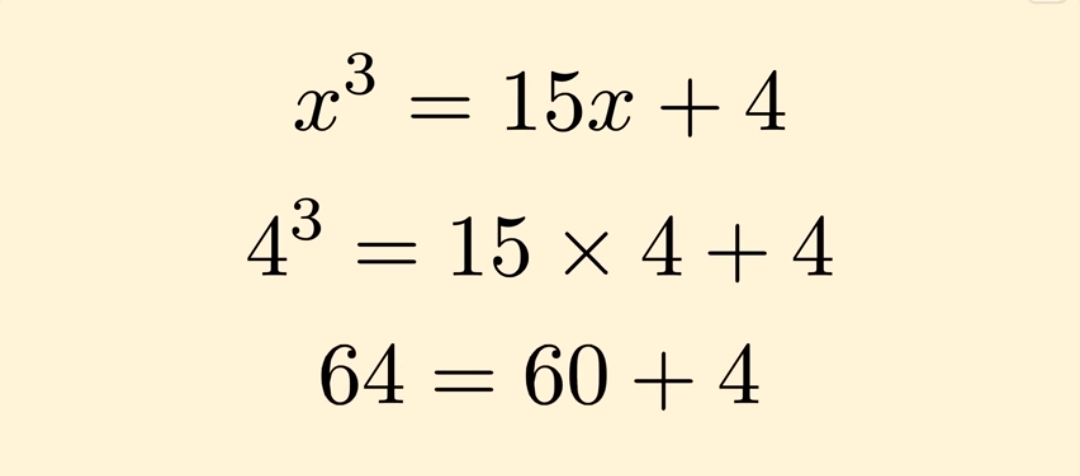
Так почему же способ, который до этого всегда работал на кубических уравнениях, тут ломается? Так как сам Кардано не смог ответить на этот вопрос, он достаточно ловко увиливает от него в своей книге «Арс магна», говоря, что корни из отрицательных чисел просто не имеют смысла, бесполезно их извлекать.
Через 10 лет после Кардано Рафаэль Бомбе, итальянский инженер, продолжает его работу, ничуть не пугаясь корней из отрицательных чисел и, так сказать, отбрасывая геометрическую интерпретацию арифметики.
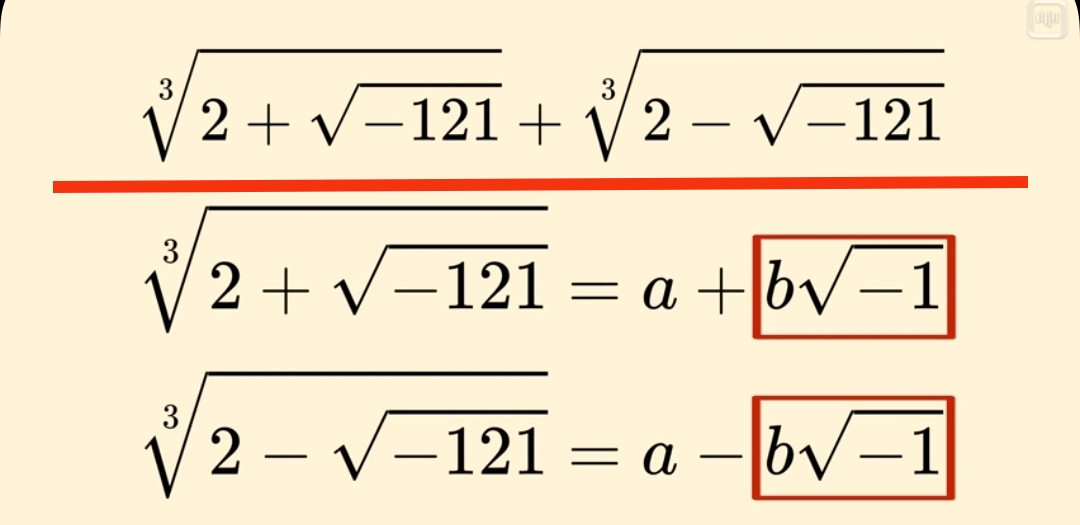
Он пытается найти решение у этой задачи, зная, что корень из отрицательного числа не является ни положительным, ни отрицательным. Он проводит некоторые вычисления, которые включали в себя произведения обычных чисел с комплексными, как мы называем их сейчас, и с помощью такого произведения обычного числа с корнем из отрицательного числа Бомбе находит решение этого кубического уравнения.
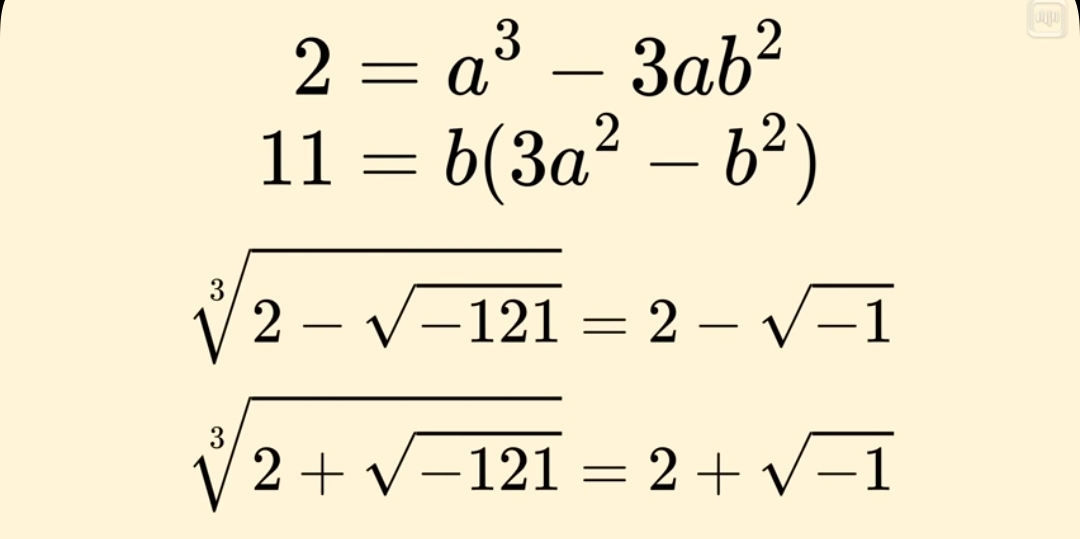 Это выглядит как настоящее чудо! То есть оказывается, что метод Кардано работает, но при этом нужно забыть про геометрическую интерпретацию уравнений и в некотором смысле формально работать с корнями из отрицательных чисел.
Это выглядит как настоящее чудо! То есть оказывается, что метод Кардано работает, но при этом нужно забыть про геометрическую интерпретацию уравнений и в некотором смысле формально работать с корнями из отрицательных чисел.
Отрицательные площади, которые до этого не существовали, должны быть просто промежуточным шагом для получения решений таких уравнений.
Благодаря Бомбе последующие несколько сотен лет математика начинает активно преобразовываться. Франсуа Виет вводит символические обозначения для алгебры, что приводит к завершению традиции решения математических проблем с помощью слов и рисунков.
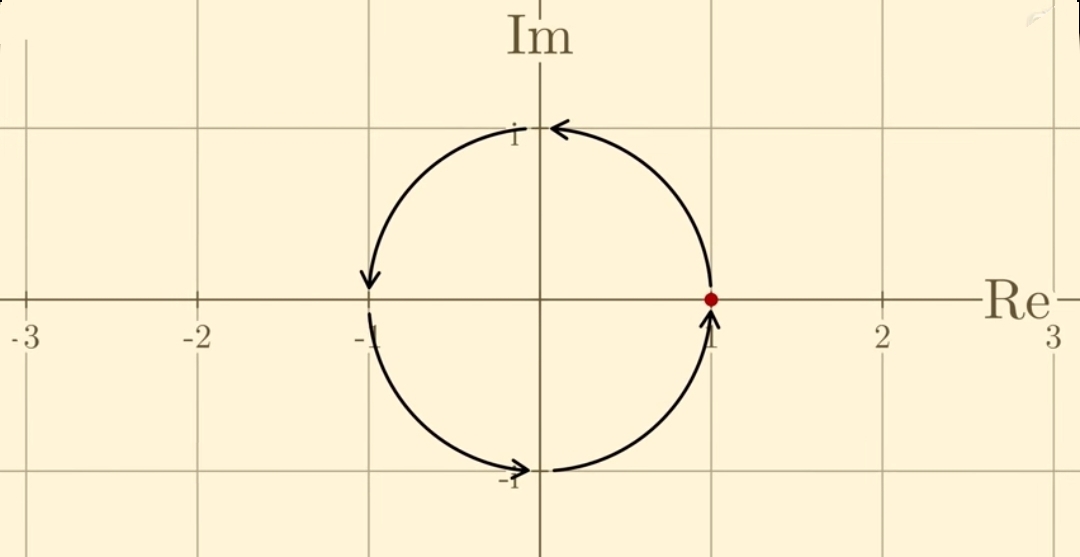
Рене Декарт часто использует корни из отрицательных чисел в своих работах, что приводит к их популяризации. Несмотря на то что он осознаёт их пользу, он называет их nombres imaginaires (воображаемые/мнимые числа). Так получилось, что это название к ним прилипло.
В дальнейшем Леонард Эйлер представляет корень из минус единицы как уже хорошо нам известную букву i.

При сложении обычных чисел и буквы i появляется новый вид чисел — комплексные.
Именно кубические уравнения привели к появлению таких чисел, и это способствовало отделению алгебры от геометрии. Это был очень важный шаг в истории математики, и именно эта идея в дальнейшем привела к формулам для нахождения всех трех решений кубического уравнения. Это было только началом.
Переоценить пользу мнимых чисел очень сложно. Да просто невозможно! Кстати, помните, мы говорили про одну физическую теорию, которая базируется, основывается на мнимых числах? Так вот, они используются в уравнении Шрёдингера — основном уравнении квантовой механики, и именно они во многом определяли развитие физики, химии и электротехники.
Достаточно вспомнить фазовые диаграммы — они есть в каждом учебнике по электротехнике, и вы можете быть уверены, что мнимые числа сыграли не последнюю роль и ещё найдут много применений. А кому же находить эти применения, как не вам, дорогие прикладники, дорогие наши ученики, товарищи? Ну а на сегодня всё! Не забываем ставить лайки, подписываться на канал и оставлять комментарии. Это поможет продвижению этого видео, чтобы оно попало в рекомендации к интересующимся людям. Ну а в комментариях можете написать, что из сегодняшнего видео вы узнали нового. Я, например, из этого видео, честно скажу, знал не всё, хотя и достаточно глубоко интересуюсь историей математики. Так что будем рады обратной связи!
Известная дружба Леонардо да Винчи и математика Луки Пачоли, завязавшаяся во время их службы у Миланского герцога Лодовико Моро в 1496-1499 гг. Сведения об их творческом сотрудничестве сохранились в трудах Луки Пачоли, в частности в его сочинении "О божественной пропорции", а также в недавно опубликованной рукописи "О возможностях чисел" ("De viribus quantitatis"). Несколько упоминаний о Пачоли содержат записи Леонардо. Они важны для понимания роли известного математика в совершенствовании математических знаний Леонардо, не получившего, как известно, систематического образования. В отечественной историографии творческое содружество двух ярчайших деятелей итальянского Возрождения не было предметом специального исследования (1). В обширной зарубежной литературе о Леонардо да Винчи крайне мало, однако, работ о его связях с Лукой Пачоли (2). Нам эта тема представляется заслуживающей особого внимания.
Сведения о биографии Луки Пачоли скудны. Родился он около 1445 г. в Богро Сан Сеполькро (близ Ареццо) в пополанской семье. Здесь начались его занятия математикой в мастерской знаменитого художника и математика Пьеро делла Франческа. В 1464 г. Пачоли получил место преподавателя математики в доме венецианского купца Антонио Ромпиачи. В Венеции он посещал публичные лекции по математике Доменико Брагадино, а в поездках на Ближний Восток (за счет Ромпиачи) получил возможность познакомиться с весьма развитыми здесь математическими науками. В Венеции Пачоли написал первую работу по математике - учебник по коммерческой арифметике (ныне утрачена). С 1470 г. Пачоли жил в Риме, где был принят (не позднее лета 1471 г.) в доме Леона Баттиста Альберти как почетный гость. Дружба с Альберти, известным гуманистом, архитектором и математиком, повлияла на научные взгляды Пачоли. Спустя много лет он напишет в сочинении "О божественной пропорции" об Альберти как "о человеке великой проницательности и учености" (3).
В 1477 г. Пачоли принял монашеский сан, вступив в орден францисканцев-миноритов (теперь он именовался фра Лука из Борго), что позволило ему читать лекции в школах и университетах Италии. Он стал странствующим профессором математики (таков был его официальный статус) и в течение многих лет читал курс по арифметике и алгебре в университетах Перуджи, Рима, Неаполя, Флоренции. В 1486 г. фра Лука из Борго получил степень доктора теологии и начал готовить сводный труд по математике, который завершил в 1493 г. В 1494 г. при его непосредственном участии была напечатана в Венеции в типографии Паганино Паганини "Сумма арифметики, геометрии, учения о пропорциях и отношениях". Второе издание "Суммы" вышло в 1523 г., и в течение полувека труд Пачоли был самым обстоятельным и читаемым сочинением по математике. "Сумма" содержала ряд трактатов по арифметике, алгебре, а также о впервые изложенной им теории и практике двойной бухгалтерии, предназначенной для оформления торговых книг.
Написанная на итальянском языке, "Сумма" сразу принесла Пачоли славу ученого-математика. Книгой заинтересовался и Миланский герцог Лодовико Моро (Лодовико Сфорца), решивший пригласить автора для чтения лекций по математике в университете Павии (расположенная недалеко от Милана, Павия была в те времена главным научным центром герцогства). Пачоли принял предложение Лодовико Моро, предоставившего ему кафедру математики. Его лекции начал посещать Леонардо да Винчи, служивший у герцога в качестве инженера-мелиоратора (4). В Милане Пачоли начал работу над сочинением "О божественной пропорции", иллюстрации к которой попросил сделать Леонардо.
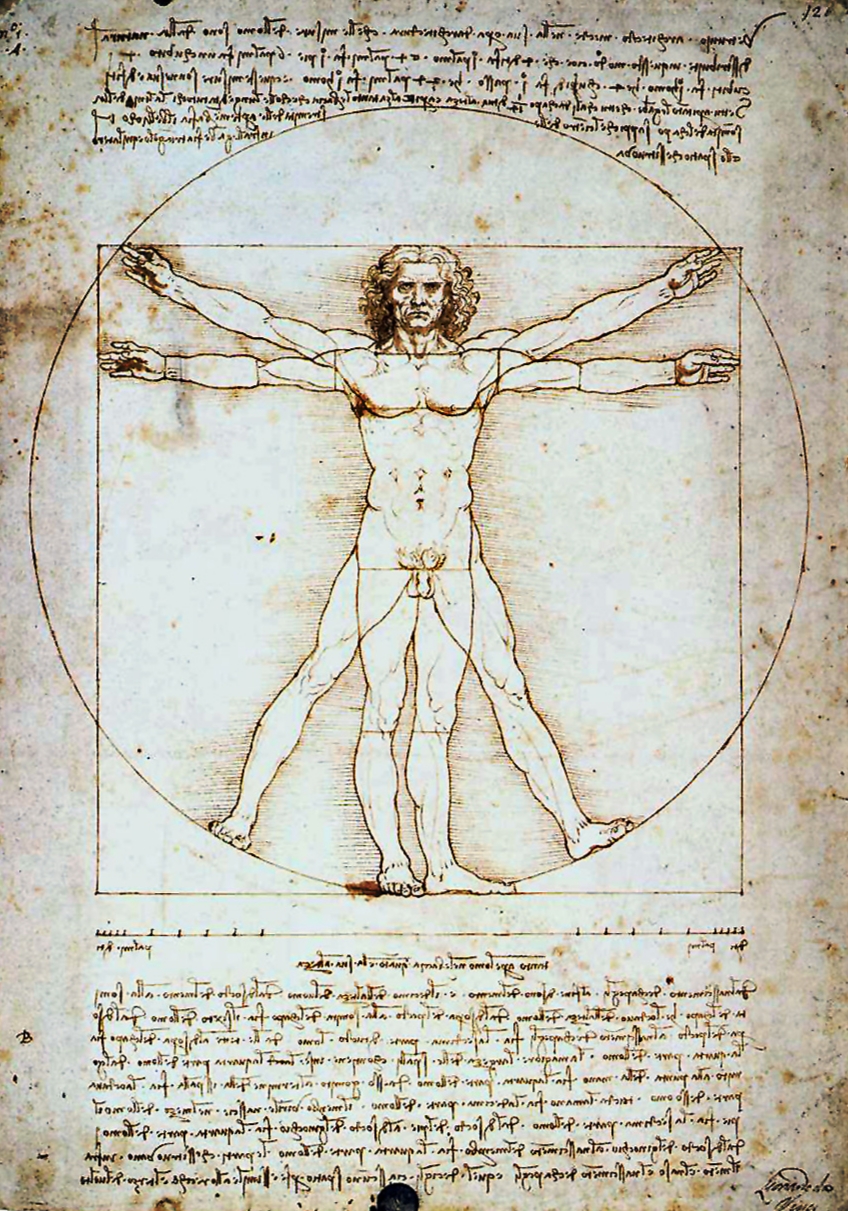
Золотые пропорции человека, «Vitruvian Man». Леонардо да Винчи (1451—1519) вместе с Фра Лука Пачоли (1445—1514), одним из ведущих ученых Ренессанса, были увлечены золотым сечением и вместе написали диссертацию «The Divine Proportion (Божественная пропорция)» , которая была опубликована в Милане в 1509 с иллюстрациями Леонардо. Среди изобилия исследований да Винчи в одном из его журналов Vitruvius's De Architectura есть знаменитый «Vitruvian Man» — изучение пропорций человека. Этот рисунок и сопровождающий текст иногда называют «Canon of Proportions (канон пропорций)» (1492, перо, чернила, акварель, бумага, 34.3 х 24.5 см., Gallerie dell'Academia в Венеции). Леонардо изображает обнаженную мужскую фигуру в двух наложенных положениях с разведенными руками, одновременно вписанную и в круг, и в квадрат. Центр круга, находящийся в пупке, делит тело на большую и меньшую верхнюю часть в золотой пропорции. Вероятно, да Винчи был первым, кто назвал эту пропорцию «золотое сечение» (лат. «sectio aurea»).
Природа распорядилась в строении человеческого тела следующими пропорциями: длина четырёх пальцев равна длине ладони, четыре ладони равны стопе, шесть ладоней составляют один локоть, четыре локтя — рост человека. Четыре локтя равны шагу, а двадцать четыре ладони равны росту человека. Если вы расставите ноги так, чтобы расстояние между ними равнялось 1/14 человеческого роста, и поднимите руки таким образом, чтобы средние пальцы оказались на уровне макушки, то центральной точкой тела, равноудаленной от всех конечностей, будет ваш пупок. Пространство между расставленными ногами и полом образует равносторонний треугольник. Длина вытянутых рук будет равна росту. Расстояние от корней волос до кончика подбородка равно одной десятой человеческого роста. Расстояние от верхней части груди до макушки составляет 1/6 роста. Расстояние же от верхней части груди до корней волос — 1/7. Расстояние от сосков до макушки составляет ровно четверть роста. Наибольшая ширина плеч - восьмая часть роста. Расстояние от локтя до кончиков пальцев — 1/5 роста, от локтя до подмышечной ямки — 1/8. Длина ладони — это 1/10 роста. Начало гениталий находится как раз посредине тела. Стопа — 1/7 часть роста. Расстояние от мыска ноги до коленной чашечки равно четверти роста, а расстояние от коленной чашечки до начала гениталий также равно четверти роста. Расстояние от кончика подбородка до носа и от корней волос до бровей будет одинаково и, подобно длине уха, равно 1/3 лица
отсюда
Их творческое сотрудничество привело к тесной дружбе, так что, когда Милан в 1499 г. был взят французами (в 1494 г. начались Итальянские войны), они вместе покинули город и отправились сначала в Венецию, а затем во Флоренцию. В 1506 г. Леонардо вернулся в Милан, где стал служить у короля Людовика XII, а Пачоли в течение нескольких лет жил во Флоренции, но ездил читать лекции в университеты Пизы, Перуджи, Болоньи. В 1508-1510 гг. Пачоли находился в Венеции, где готовил к изданию свой перевод сочинений Евклида по геометрии. В 1510 г. Пачоли в Перудже читал лекции по математике, а в 1511 г. вернулся на родину, в Борго Сан Сеполькро, где стал настоятелем францисканского монастыря. Однако слава Пачоли-математика по-прежнему была велика: в 1514 г. папа Лев X пригласил его в Рим для чтения лекций. В 1517 г. Пачоли скончался и был похоронен в Борго Сан Сеполькро, в церкви Сан Джованни (5).
В мастерской Пьеро делла Франческа, где он обучался в юности, и позже Пачоли многое черпал из практики инженерного и художественного ремесла. И свои труды по математике он рассматривал как возможный ответ науки на сложные задачи, выдвигавшиеся практикой. Эту позицию раскрывают его собственные признания в предисловиях к "Сумме" и сочинению "О божественной пропорции". Об этом свидетельствует и чрезвычайно широкое распространение его трудов, написанных на итальянском, а не на латыни, как это было принято в науке той поры. Показательно, что в "Сумме" некоторые разделы он давал в латинском и итальянском вариантах. Пачоли мечтал освободить науку - а главной в ней он считал математику - от схоластической абстрактности и обогатить практику научной теорией. Поэтому итальянский язык для сочинений по прикладной математике он выбирал не случайно: практикам он был более доступен, чем латынь.
Вдохновляла Пачоли и другая идея - стремление показать универсальный характер математических знаний, математики как "всеобщей закономерности", которую можно применить ко всем вещам. Это убеждение фра Луки основывалось на философии Платона, его учении о математике как некоем опосредующем звене между миром идей и материей, а также на неоплатонизме Марсилио Фичино и Джованни Пико делла Мирандола, проникнутом пифагорейскими и каббалистическими представлениями о роли числа. Однако его мало привлекал в целом умозрительный характер философии флорентийских неоплатоников (6).
Как показал Л. Ольшки, Пачоли был хорошо знаком с математическими идеями Платона по его "Тимею". По примеру пифагорейцев Платон полагал, "что четыре или пять стихий состоят из правильных тел. Он представлял себе, что однородная, составляющая тело мира материя, сгущаясь известным образом в небольшие, невидимые тетраэдры, образует стихию огня, а в гексаэдры - стихию земли... Между этими крайними телами помещались затем в виде связующих звеньев икосаэдр и октаэдр, причем первый получил форму стихии воды, а второй форму стихии воздуха. Пятое из правильных тел, додекаэдр, представляло, по мнению пифагорейцев, эфир и символизировало у Платона упорядоченную форму мирового целого. Переход одной стихии в другую изображался в виде преобразования правильных тел друг в друга. Таким образом платоновская физика сливалась со стереометрией" (7). И у Пачоли, разделявшего эти пифаогорейски-платоновские представления, стереометрия оказывалась главным звеном его математических изысканий.
Античные идеи легли в основу учения о пропорции, которому Пачоли уделял особое внимание. В "Сумме" он отмечал: философы "хорошо знали, что без учения о пропорции невозможно познание природы; действительно, всякое наше исследование направлено на то, чтобы установить отношение вещей друг к другу" (8). Пачоли была близка высказанная в "Тимее" мысль Платона, что с пропорциями мы имеем дело "не только в области чисел и измерений, но и в музыке, в географии, в определении времени, в статике и Динамике, во всех, следовательно, искусствах и науках" (9). На точном знании пропорций покоится линейная и воздушная перспектива, равно как и правдивое изображение человеческого тела. Особый интерес Пачоли проявлял к архитектурным пропорциям: в возведенной Брунеллески церкви Сан Лоренцо во Флоренции он видел наиболее совершенный пример правильного Применения пропорции в современном ему зодчестве (10).
Главная посылка философских взглядов Пачоли - идея рациональности божественного творения, к которой причастен и человеческий ум. Выражением рациональной связи между Богом, миром и человеком является число, поэтому и познание структуры вещей, т.е. наука, обращено к изучению количественных закономерностей, а значит, связано с математикой, полагал он.
Пачоли мечтал сделать учение о пропорции доступным для практического применения в работе художников и архитекторов. Уже в "Сумме" этой энциклопедии математических знаний, он поднимает вопросы, основательно забытые в средние века, но актуальные для технических и художественных ремесел эпохи Возрождения (11). Он воскрешает интерес к геометрии, особенно к учению о многогранниках, а также формулирует ряд важных положений об универсальности пропорций, о пропорциональности как натурфилософской закономерности. Этот труд свидетельствует об огромной научной эрудиции Пачоли-математика, хорошо знакомого с сочинениями Евклида и Боэция, Леонардо Пизано (Фибоначчи) и Бьяджо Пелакани да Парма, Джордано Неморарио и Региомонтана, равно как и глубокие познания в области философии. В учении о пропорции он опирается не только на Евклида и Боэция, но подкрепляет теоретическую часть ссылками на Платона, желая подчеркнуть значение пропорциональности как принципа природы, как естественного и эстетического канона. Такая "спаянность" математики и философии была присуща не только "Сумме" Пачоли, но и другому значительному его сочинению - "О божественной пропорции" и может рассматриваться как принцип научного метода фра Луки из Борго.
"О божественной пропорции" - математический труд, специально посвященный рассмотрению проблем, в решении которых нуждались инженеры и художники: это проблемы пропорции и построения правильных многоугольников и многогранников. Интерес к ним Пачоли проявил и в "Сумме", но в этой работе он усилил философскую основу математической теории, демонстрируя приверженность платоновско-пифагорейской концепции чисел (12).
Книга "О божественной пропорции", написанная Пачоли в Милане (он завершил ее в 1498 г.), была напечатана позже, в 1509 г., в Венеции. 60 цветных иллюстраций к ней выполнил по просьбе Пачоли Леонардо да Винчи. Иллюстрации представляли собой комплекс трехмерных рисунков в стереометрии.

Пачоли хвалит их как "выполненные весьма совершенно в перспективном построении" (13). Среди этих рисунков были так называемые правильные тела - пять многогранников, которые Платон определял как формы пяти естественных элементов: пирамида - огня, куб - земли, додекаэдр - неба, октаэдр - воздуха, икосаэдр - воды. Леонардо нарисовал их во всех возможных вариантах. Безусловно, столь мастерски выполненные иллюстрации повышали научную ценность книги и делали ее более привлекательной для читателя.
Сочинение "О божественной пропорции" состоит из трех частей: "Компендия о божественной пропорции", "Трактата об архитектуре" и "Небольшого трактата в трех частях". В первой части, воздав хвалу математике, Пачоли излагает теорему о "божественной пропорции", смысл которой заключается в следующем: постоянная пропорция возникает при таком разделении сегментов на две части, когда квадрат, построенный на большей его части, равен прямоугольнику, имеющему в качестве сторон весь сегмент и меньшую его часть. Такая пропорция известна как "золотое сечение". Пачоли именует эту математическую закономерность "превосходной", "божественной" пропорцией, усматривая в ней ряд черт, сходных с высшей божественностью. Это, во-первых, единичность, или исключительность, Бога; во-вторых, его троичность и соответственно наличие трех пределов в пропорции; наконец, неизменность Бога и пропорции; отмечает он и другие подобия. Превосходные свойства данной пропорции подчеркиваются, по мысли Пачоли, и безграничностью ее возможностей, поскольку, не зная ее, невозможно обнаружить многого, достойного восхищения, как в философии, так и в других науках (14).
Принцип золотого сечения был открыт в древности, возрождён в период Ренессанса и до сих пор является одним из самых известных изобразительных канонов. Скептики считают его популярным мифом, а последователи — раскрытым секретом идеала.
Правило золотого сечения
Золотое сечение — это такое отношение частей к целому, когда большая часть относится к меньшей так же, как целая к большей. Это отношение составляет 1,618. У прямоугольника, построенного по этому правилу, меньшая сторона будет 1, а большая — 1,618. Линия горизонта будет располагаться не посередине работы, а чуть выше. В процентном значении части будут относиться друг к другу как 62% на 38%.
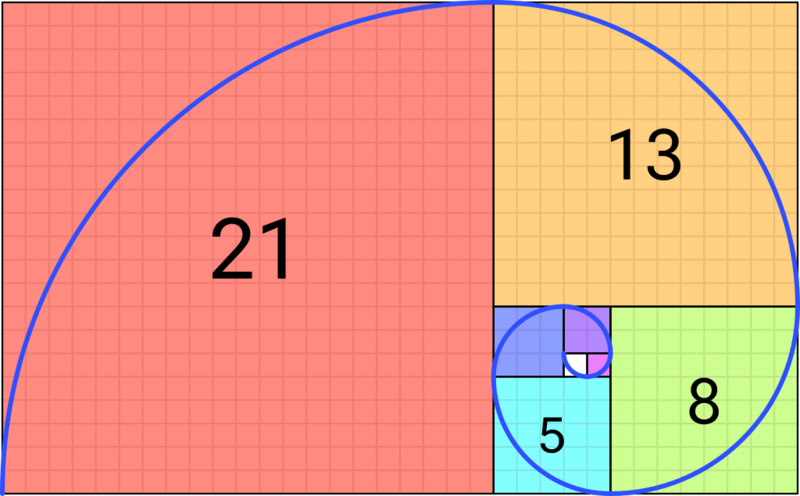
отсюда
Изученная ещё в работах математиков и философов Древней Греции, формула золотого сечения снова стала властвовать над умами творцов в период Возрождения. Этому есть объяснение — закончилось время, которое мы сегодня знаем как Средние века: мышление человека перешло из плоскости мистического в рациональное. Всё можно объяснить математически, научно и даже зыбкое понятие прекрасного разложить на составляющие — в этом были уверены передовые художники Возрождения.
В то время теорию золотого сечения выразил монах Лука Пачоли в книге «Божественная пропорция» (1509), иллюстрации к которой создал Леонардо да Винчи. Пачоли видел в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой — Отца, а целое — Святой дух.
Леонардо да Винчи применял этот изобразительный принцип в своём творчестве. Его «Тайная вечеря» вся состоит из элементов, вписанных в геометрические фигуры, построенные по правилу золотого сечения.

Изображение: Dr. Elliot McGucken
После да Винчи в картинах мастеров золотое сечение стало основой композиции. Процесс создания живописного полотна уже не обходился без решения геометрических задач: например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретённый им пропорциональный циркуль.
Примеры работ с применением правила золотого сечения
Древние египтяне явно владели знаниями о правиле золотого сечения (которое тогда так ещё, конечно, не называлось) — об этом свидетельствует пирамида Хеопса, возраст которой оценивается примерно в 4500 лет. Соотношение высоты пирамиды Хеопса к основанию равняется 14/22, что очень близко к каноническому соотношению.
Древнегреческий Парфенон — памятник античной архитектуры, расположенный на афинском Акрополе, — также был построен в соответствии с этим принципом. Отношение высоты к ширине фасада храма приближается к числу 0,618. Те же соотношения прослеживаются в древнеримских арках и акведуках, их замечают в сводах Сикстинской капеллы.

Фасад Парфенона идеально вписывается в канон
Фото: Wikimedia Commons
Принципы золотого сечения его адепты отмечают в природе: в рисунке раковин моллюсков, в расположении лепестков в цветке, семян подсолнечника, в узорах паутины и в форме куриного яйца.
Альтернативные концепции красоты
Сейчас обоснованность использования принципа золотого сечения подвергается критике. Не существует ни одного научного эксперимента, который бы доказывал, что этот канон действительно эстетически более притягателен для человеческого глаза, чем какое-либо другое сочетание пропорций и измерений.
Кит Девлин, профессор математики Станфордского университета, — один из главных скептиков его ценности. Он считает, что многие исследователи слишком часто искали золотое сечение там, где оно не предполагалось, и выдавали приближенные значения за точные. Девлин называет золотое сечение мифом поп-культуры.
В мире возникали и альтернативные концепции «поиска» красоты. Например, древнегреческий скульптор Поликлет создал трактат, в котором описывал правила, по которым можно точно построить изображение человеческого тела. По расчётам скульптора, главная мера, которой нужно оперировать, — отношение размера головы к росту всей фигуры: в идеальном теле оно должно составлять пропорцию 1:8.
Построение частей тела, по Поликлету, также вычислялось по формуле, в основе которой лежали пифагорейские соотношения большого квадрата на диагонали малого квадрата. Чтобы визуализировать свой канон, Поликлет создал статую «Дорифор» («Копьеносец») — воплощённый в бронзе пример мужского тела.

Статуя «Дорифор» из Национального археологического музея Неаполя. Оригинал в бронзе не сохранился: нам доступны только реконструкции и реплики
Фото: Wikimedia Commons
Один из основоположников модернизма, архитектор Ле Корбюзье разработал собственную систему пропорционирования, которая отталкивалась от замеров тела взрослого человека, но одновременно опиралась на шкалу «золотых отрезков». Он применял её при проектировании сооружений.
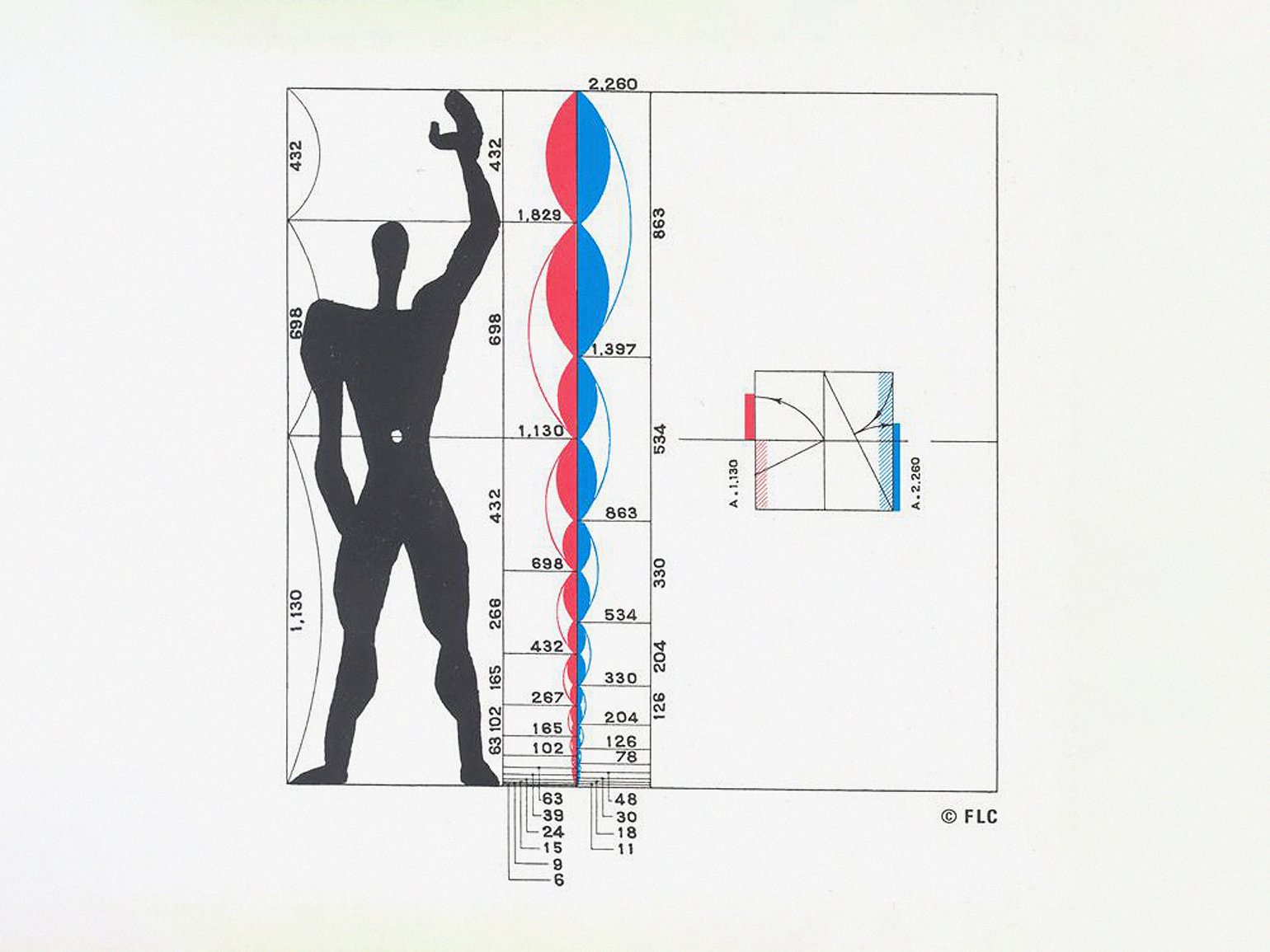
Система пропорций Ле Корбюзье называется Le Modulor — модулёр или модюлор
Изображение: Fondation Le Corbusier
Золотое сечение в современном дизайне
Простейшее правило идеальной пропорции, которое мы чаще всего видим на картинах, макетах, полиграфической продукции, — деление пространства на девять частей. Поворачивая прямоугольник макета в каждом из направлений по вертикали и горизонтали, проводится линия по каноническим пропорциям 62% на 38%. Если объяснять проще: линия на листе проходит не посередине, а чуть выше. Лист нужно перевернуть и снова нарисовать линию, и так четыре раза. В точках пересечений линий располагают композиционно значимые элементы — именно туда прежде всего падает взгляд зрителя.
Часто правило золотого сечения применяют и при создании макета. Макет, ширина и высота которого находятся в «золотой» пропорции 1,618 (960 на 594 пикселя), разбивается на две части с соотношением 1 к 1,168: большую и меньшую.
Основное изображение и текст ставят в больший прямоугольник так, чтобы пространство или «воздух» между ними располагались по невидимым линиям золотого сечения. «Шапка» журнала, подписи под фотографиями, адрес в письмах располагаются в меньшем прямоугольнике.

Модульная сетка, построенная на основе канона
Источник: BONT / Adrián Somoza / Dribbble
Если следовать логике скептиков, то золотое сечение можно тем или иным способом найти в любом удачном дизайне. Сообщить о популярной концепции иногда полезно при разговоре с заказчиком, во время публичной защиты своего проекта. Работает ли золотое сечение или его значение сильно преувеличено — об этом до сих пор спорят художники и дизайнеры.
skillbox - Мария Лащева
Рассмотрев 13 следствий из теоремы о постоянной пропорции, Пачоли переходит к изложению принципов построения правильных многогранников, доказывая, что их существует в природе только пять. Он определяет отношение между сторонами правильных многогранников и диаметром сферы и исследует, каким образом можно вписать один многогранник в другой. Правильные тела Пачоли вслед за Платоном соотносит с основными элементами - стихиями мира: землей, водой, огнем, воздухом и небом (15).
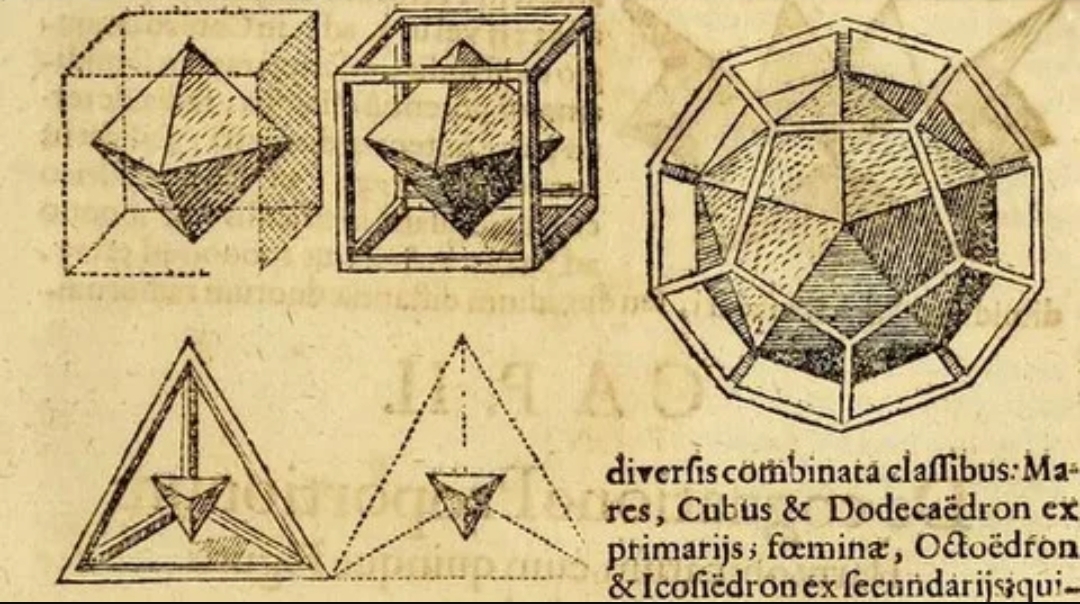
Во второй части сочинения Пачоли ведет речь о колоннах, пирамидах, конусах и принципах их построения преимущественно на основе теории Витрувия, что имело важное значение для архитектурной практики того времени. Популярность архитектурной теории Витрувия была связана в значительной мере с публикацией в 1485 г. труда Альберти "О зодчестве". Пачоли обращает особое внимание на заключенный в архитектурных формах принцип красоты, выражающийся в "божественной пропорции". В приложении к своему сочинению он дает перевод с латинского на итальянский язык трактата "О пяти правильных телах" Пьеро делла Франческа, опубликованного в 1507 г. В трактате содержались указания на практическое применение теорем Евклида о правильных телах, было показано, как измерять и строить стереометрические тела (многогранники, сферы и т.д.). Все это прямо отвечало запросам зодчих и художников, что и побудило Пачоли включить перевод трактата своего учителя, к которому он всегда относился с большим почтением, в книгу "О божественной пропорции". Появились обвинения Пачоли в плагиате (первым это сделал Дж. Вазари), но следует заметить, что традиция создания научных трудов не исключала подобного рода включений. К тому же Пачоли осуществил перевод трактата Пьеро дел-ла Франческа во имя благой цели - сделать его более доступным для художников и архитекторов, которым прежде всего была предназначена его книга, о чем гласит ее подзаголовок (16).
Свой последний значительный труд по математике - "О возможностях чисел" ("De viribus quantitatis") - Пачоли завершил в 1508 г., подготовив рукопись к изданию, но по каким-то причинам не смог этого сделать. Впервые она была опубликована только в 1997 г. Это сочинение содержит арифметические и геометрические задачи, математические игры и разного рода загадки, Пословицы, басни (17). Этот труд Пачоли также предназначал для практическо го использования и писал его на итальянском языке, хотя, впрочем, не слишком совершенном. Здесь он вновь воздает хвалу рисункам Леонардо, сделанным для его книги "О божественной пропорции". Леонардо создал прекрасные фигуры многогранников - "высочайшего (уровня) легчайшие фигуры всех платоновских и математических тел, как правильных, так и производных (зависимых), рисунки которых выполнил в изометрической перспективе столь совершенно, что лучше сделать было бы невозможно, даже если бы к нам вернулись Апеллес, Мирон, Поликлет и другие" (18). И ностальгически замечает, что Леонардо выполнял рисунки "в те счастливые времена, когда мы вместе находились на службе в восхитительнейшем городе Милане" (19).
Это были годы тесного сотрудничества Пачоли и Леонардо. Чтобы выполнить свое обязательство по созданию иллюстраций к книге Пачоли, Леонардо должен был познакомиться с принципами построения правильных многогранников и с теорией пропорций в целом. Л. Рети обращает внимание на тот факт, что именно начиная с 1496 г. в рукописях Леонардо много места занимает геометрия. В манускрипте М и I, который датируется 1496-1499 гг., сотня страниц посвящена изучению первых книг и отчасти десятой книги "Элементов" Евклида. По мнению исследователя, в этом можно видеть несомненное свидетельство влияния Пачоли (20). В Милане Пачоли работал над переводом "Элементов" Евклида, так что вполне возможно предположить, что он консультировал Леонардо по проблемам геометрии, во всяком случае поддерживал его интерес к этой области математики. Впрочем, Леонардо да Винчи еще в молодости, во Флоренции, занимали проблемы перспективы, связанные с геометрией. Увлекала Леонардо и теория пропорций, овладеть которой он считал важной задачей для себя как художника. Размышлял он и о теоретической стороне пропорциональности. В пропорции он видел основу числовой гармонии, присущей мирозданию, и полагал, что она составляет суть "не только числа и размера, но также звуков, веса, времени и места, любой существующей в мире силы" (21).
Леонардо считал необходимым органическое соединение эксперимента с его математическим осмыслением - в этом он был пионером современного естествознания. Математика, по Леонардо, главная наука, способная придать результатам эксперимента достоверность и получить однозначную истину. Поэтому механику он называл раем математических наук. Такая позиция была близка к Пачоли, который полагал, что математика должна выражать всеобщую закономерность, применимую ко всем вещам. В сочинении "О божественной пропорции" он подчеркивал, что "математические науки наиболее истинны и имеют первую степень достоверности, им следуют и все другие естественные науки" (22). Леонардо отмечал в записках: "Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой"; "Пусть не читает меня в основаниях моих тот, кто не математик" (23).
Архимед и Евклид - античные столпы математики - были известны и в средние века, хотя к их трудам проявляли интерес скорее в плане теории, не в практическом преломлении. В эпоху Возрождения они стали основой не только для развития математической теории, но и широко использовались в прикладных целях, особенно труды Евклида. Сочинения Архимеда и Евклида хорошо знал Пачоли и часто ссылался на них. Возможно, под его влиянием они стали известны и Леонардо - ведь именно в Милане Пачоли занимался переводами Евклида. Конечно, главной школой формирования Леонардо-ученого была его практика художника и инженера. Следует помнить, что в Милане он состоят на службе у герцога в качестве инженера, ведавшего водными путями; он разработал ряд проектов по созданию каналов во владениях Лодовико Моро. Работал он по просьбе герцога и над его огромной конной статуей, что требовало детальных и точных математических расчетов. Отсюда, возможно, и интерес Леонардо к знаменитому профессору математики, лекции которого он стал посещать в университете Павии. и его стремление видеть в нем выдающегося специалиста в области прикладной математики. В записях Леонардо той поры читаем: "Научись умножению корней у маэстро Луки" (24). Есть сведения, что Пачоли помогал Леонардо в его расчетах грандиозной конной статуи Лодовико Моро. К. Педретти увидел множество перекличек в математических задачах, представленных в книге Пачоли "О возможностях чисел" (работу над ней он начал в Милане), с рукописями Леонардо времени их сотрудничества в Милане (25).
Лука Пачоли питал огромное уважение к Леонардо, высоко ценил разносторонность его таланта, о чем не раз упоминал в книге "О божественной пропорции". Так, говоря об авторе иллюстраций к ней, он пишет: `Таковые были сделаны достойнейшим живописцем, перспективистом, архитектором, музыкантом и всеми талантами одаренным Леонардо да Винчи" (26). Он писал о Леонардо как о "ненасытном в занятиях живописью, конструировании и ваянии" и завершившем уже "с всемерным старанием книгу о живописи и книгу о движении человеческого тела" (27). Пачоли выделял Леонардо среди яркого окружения герцога Лодовико Моро, при дворе которого работали выдающиеся художники, архитекторы, ученые (например, архитектор Браманте, историки Корио и Мерула, ученый Фацио Кар-дано и ряд других) (28). Изваянную статую герцога он называл "грандиозной и восхитительной", а "книгу о локальном движении от толчка и тяжести", над которой Леонардо работал в Милане, "бесценным трудом" (29). Дружбу Пачоли и Леонардо крепило тесное научное сотрудничество, взаимное глубокое уважение, совпадение позиций по многим проблемам науки. Судьба развела их в последние годы жизни, но взаимные симпатии и уважение сохранились, о чем свидетельствуют, в частности, последняя работа Пачоли "О возможностях чисел" и тот факт, что подлинники иллюстраций Леонардо он хранил у себя до конца дней (30). И если Леонардо да Винчи прославил эпоху Возрождения как ее универсальный гений, то Лука Пачоли стал выдающимся специалистом в одной области, подведя первые итоги развитию ренессансной математики. И в этом тоже была притягательная сила, способствовавшая их сближению и сотрудничеству
1 - Эта тема затронута лишь в работе: Зубов В.П. Леонардо да Винчи. 1452-1519. М.; Л 1961.
2 - См.: Ольшки Л. История научной литературы на новых языках. М.; Л., 1933. Т. 1; Raulich Н. Fra Luca Pacioli. Pr., 1940; Ricci DJ. Luca Pacioli, l`uomo e lo scienziato Sansepolcro, 1940; Pedretti C. Studi Vinciani: Documenti, analisi e inediti leonardeschi. Geneve 1957; Hart IB. The world of Leonardo da Vinci. L., 1962; The unknown Leonardo / Ed. By L. Red. N.Y., 1974; Kemp M. Leonardo da Vinci: the marvellous works of nature and of man. L. 1981.
3 - Цит. по: Гарэн Э. Проблемы итальянского Возрождения. М., 1986. С. 193.
4 - См.: Malaguzzi-Valeri Fr. La corte di Lodovico il Moro. Milano, 1915.
5 - В 1878 г. в Сансеполькро был воздвигнут памятник Пачоли. Надпись на нем гласит: "Луке Пачоли, который был другом и советником Леонардо да Винчи и Леона Баттиста Альберти, который впервые придал алгебре язык и структуру науки, который применил свое великое открытие к геометрии, а также изобрел двойную бухгалтерию".
6 - Как справедливо замечает В.Н. Лазарев, "Пачоли не довольствуется чистой символикой чисел. Математика приобретает в его глазах и самостоятельное, практическое значение" (Лазарев В.Н. Пьеро делла Франческа. М., 1966. С. 16).
7 - Ольшки Л. Указ. соч. С. 141-142.
8 - Там же. С. 122.
9 - Там же. С. 123.
10 - Там же.
11 - Pacioli L. Summa de arithmetica, geomctria, proportion e proportionalita. Kyoto, 1973. P. 2 (факсимильное изд. 1494 г.).
12 - Pacioli L. De divina proportione. Milano, 1956, а также: Urbano, 1969. Наш перевод на русский язык отрывков из сочинения Пачоли "О божественной пропорции" см. в кн.: Эстетика Ренессанса: В 2 т. М., 1981. Т. 2. С. 373-387. В 5-й главе Пачоли излагает взгляды Платона на математическую структуру мироздания и говорит о пяти правильных телах, соответствующих мировым стихиям (Там же. С. 377-378).
13 - Pacioli L. De divina proportione. P. 137.
14 - Пачоли Л. О божественной пропорции // Эстетика Ренессанса. Т. 2. С. 377-378. См.: "Commo senza la notitia de dicta proportione molte cose de admiratione dignissime in philosophia ne in alcun`altra scientia potrieno havere" (Pacioli L. De divina proportione. P. XV).
15 - См.: "Итак, указанные тела называются правильными, потому что у них равные стороны, углы и основания и при этом каждое из них содержится в другом, как это будет показано. Они соответствуют пяти простым телам самой природы, то есть земле, воде, воздуху, огню и пятой сущности - небесной силе, которая заключает в себе все прочие (тела. -Л.Б-)" (Эстетика Ренессанса. Т. 2. С. 383).
16 - В предисловии к "Трактату об архитектуре" (в составе книги "О божественной пропорции") Пачоли пишет, что хотел привести доказательства по вопросам перспективы "своего земляка и современника, главного знатока и учителя - Пьеро делла Франческа" (цит. по: Pedretti С. Op. cit. P. 45. Перевод наш).
17 - Pacioli L. De viribus quantitatis / Trascrizione di Maria Garlaschi Peirani dal codice n. 250 della Biblioteca Universitaria di Bologna. Prefazione e direzione di Augusto Marinoni. Milan, 1997.
18 - См.: "...con le supreme et legiadrissime figure de tutti li platonici et mathematici corpi regulan et dependenti, che in prospectivo disegno non e possibile al mondo farli meglio, quando bene Apelle Mirone, Policreto et gli altri fra noi tornassero..." (Ibid. P. IX).
19 - Ibid. P. X.
20 - См.: The unknown Leonardo. P. 69-70.
21 - Пачолли Л. О божественной пропорции. С. 358.
22 - Ср.: "… commo le discipline mathematici sono fondamento e scala de pervenire a la notitia de ongi altura scientia" (Pacioli L. De divina proportione. P. XII).
23 - Леонардо да Винчи. Избранные произведения: В 2 т. СПб.; М., 1999. Т. 1. С. 105 (52, 53).
24 - Цит. по: Pedretti С. Op. cit. P. 44.
25 - Ibid. P. 44-45.
26 - Цит. по: Зубов В.П. Указ. соч. С. 25.
27 - Ср.: "...al`opera inextimabile del moto locale de le percussioni e pesi e de le forze tutte, cioe pesi accidentali... havendo gia con tutta diligentia al degno libra de pictura e movimenti humani posto fine - quella con ogni studio ad debito fine attende de condure" (Pacioli L. De divina proportione. P. 4).
28 - Ibid. P. XI-XII.
29 - Ibid. P. 4.
30 - Pedretti C. Op. cit. P. 44.
отсюда
** Ферро и Фиор vs Тарталья vs Кардано и Феррари

«… У меня не было другого наставника, кроме спутника бедности – предприимчивости».
Никколо Тарталья
Никколо Тарталья – итальянский математик, инженер фортификационных сооружений, геодезист, имя которого неразрывно связано с разработкой способа решения кубических уравнений в радикалах. О жизни Тарталья известно не очень много. Хотя остались его сочинения, но очень мало сведений о его жизни.
Никколо Тарталья (Niccolò Fontana, Tartaglia) родился около 1500 года в Брешиа (Италия). Настоящая его фамилия - Фонтана. Отца своего, конного почтальона, который переправлял грузы и почту между Брешии и близлежащими городами, он звал по имени Микелетто (Micheletto). Хотя семья не была богатой, отец делал всё возможное, чтобы обеспечить жену, дочь и двух сыновей.
Никколо жил во времена так называемых Итальянских войн (1494-1559), которые вели между собой Франция и Испания за право владеть Италией.
Он лишился отца в раннем детстве, тот был убит при занятии города французскими солдатами (1506).
В 1512 году, во время взятия Брешии французами, когда Никколо с матерью спасался в соборе, он получил рану в нижнюю часть лица, вследствие которой произношение его стало неправильным. Выжил он только благодаря уходу матери. Увечье на вою жизнь лишило его возможности правильно произносить слова, и его стали звать "Тарталья". Тарталья – это прозвище, от итальянского слова tartaglia – заика.
В 14 лет он пошёл к учителю, чтобы выучить алфавит, но у него кончились деньги для оплаты за обучение на букве К. После этого он украл тетрадь с прописями и стал самостоятельно учиться читать и писать, используя из-за отсутствия бумаги в качестве грифельной доски надгробные плиты. Самостоятельно он овладел латинским и греческим языками.
Пристрастившись к математике и самостоятельно овладев ей, он сдал квалификационный экзамен на звание "магистра абака" (что-то вроде учителя арифметики) и стал сам преподавать другим, а впоследствии стал известным математиком своего времени. Преподавал в университетах Вероны, Брешии и Венеции.
Около 1500 года Сципион дель Ферро, профессор университета в Болонье, нашёл способ решения уравнений третьей степени, но сохранил своё открытие в тайне - таковы были тогда научные традиции. После его смерти секретом завладел один из его учеников - Антонио Мари Фиоре.
В 1534 году, уже имея семью и по-прежнему нуждаясь в деньгах, Тарталья переехал в Венецию, где стал давать публичные уроки математики в церкви Сан-Джаниполо и опубликовал свои научные работы.
Желая прославиться и заработать деньги, Фиоре в 1535 году вызвал на диспут Никколу Тарталью.
Во времена, когда жил Тарталья, обычным делом было проведение научных поединков и турниров, на которых учёные состязались между собой в том, кто быстрее и больше решит задач, предложенных противником. Победитель получал деньги, обретал славу, ему предлагали занять почётную, хорошо оплачиваемую должность.
Никколо узнал, что Фиоре владеет секретом решения кубического уравнения, который ему сообщил его учитель дель Ферро. Тарталья сел за письменный стол и за несколько дней до диспута нашёл способ решения уравнения третьей степени.
Поединок состоялся 12 февраля 1535 года. Каждому из состязающихся надо было решить по 30 задач вида и . За два часа Тарталья справился со всеми задачами, предложенными ему Фиоре, а тот не решил ни одной задачи противника. Победа была полной. Фиоре не мог поверить происходящему и обвинил Тарталья в краже формул, но доказать ничего не смог. К Тарталье пришли слава и почёт.
Джераломо Кардано и его ученик Феррари

Известный врач из Милана Джераломо Кардано в это время писал книгу по математике. Он был разносторонне одарённым учёным: был одновременно математиком и механиком, врачом и алхимиком, хиромантом и личным астрологом римского папы. Он обратился к Тарталье с просьбой сообщить ему формулы для решения уравнений третьей степени или написать в его книге своё собственное добавление на эту тему. Тарталья отказался. Но однажды, будучи в Милане, он открыл Кардано секрет, взяв с него клятву сохранять его. Кардано торжественно поклялся..
В 1545 году Кардано опубликовал своё «Великое искусство» («Ars magna»), положившее начало современному этапу развития теории уравнений. В предисловии к книге Кардано пишет: «В наше время Сципион дель Ферро открыл формулу, согласно которой куб неизвестного плюс неизвестное равен числу. Это была очень красивая и замечательная работа... Соревнуясь с ним, Никколо Тарталья из Брешии, наш друг, будучи вызван на состязание с учеником дель Ферро по имени Антонио Марио Фиоре, решил, дабы не быть побежденным, ту же самую проблему и после долгих просьб передал её мне».
Опубликованный Кардано в работе «Великое искусство» алгоритм решения уравнений третьей степени вошёл в историю математики как «формула Кардано».
В книге «Великое искусство» Кардано опубликовал и формулы решения уравнений четвёртой степени, принадлежащие Лодовико Феррари. За несколько лет до этого Кардано взял к себе в дом слугу – 18-летнего бойкого парня Лодовико, у которого оказались блестящие математические способности. Кардано занимался его образованием; Феррари и принадлежит это выдающееся открытие. В восемнадцать лет Феррари стал профессором Миланского университета.
В конце жизненного пути Кардано написал автобиографическую книгу "О моей жизни", в которой есть такие строчки: «Сознаюсь, что в математике кое-что, но в самом деле ничтожное количество, я заимствовал у брата Никколо». Возможно, его все-таки мучила совесть.
Вопрос о том, действительно ли Тарталья независимо открыл метод дель Ферро, неоднократно обсуждался. Высказывалось предположение, что на самом деле Тарталья каким-то образом получил доступ к записям дель Ферро. В качестве косвенных доказательств этой гипотезы историки ссылались на то, что других серьёзных математических достижений у Тартальи не было. Однако прямых свидетельств в пользу указанного предположения найти не удалось.
Тарталья написал книгу, изобразив Кардано человеком, лишённым моральных принципов. За своего учителя вступился Феррари. Он вызвал Тарталью на публичный диспут по "геометрии, арифметике или связанным с ними дисциплинам, таким как астрология, музыка, космография, перспектива, архитектура и др." Завязалась горячая дискуссия, за которой следила вся Италия. Это был первый в истории науки спор о том, надо ли сохранять научные открытия в тайне. На публичном диспуте в Милане победа осталась за Феррари. Тарталья жаловался, что не смог полностью изложить свои доводы из-за беспорядка, устроенного сторонниками Феррари.
В настоящее время большинство учёных сходится на том, что первым решение кубического уравнения нашёл дель Ферро; Фиоре узнал его от своего учителя; Тарталья переоткрыл формулу дель Ферро (такое нередко бывает в науке); Кардано же дал полную и исчерпывающую теорию решения любого уравнения третьей степени.
После конфликта с Кардано и проигрыша поединка его ученику Феррари (1548), авторитет Тартальи сильно уменьшился. Последние годы он занимался переводами Архимеда и Евклида на итальянский язык.
Учеником Тартальи был другой выдающийся учёный эпохи Возрождения – Джамбатиста Бенедетти, итальянский механик, математик, астроном, теоретик музыки, считающийся одним из предшественников Галилея в построении классической механики.
Работы Тарталья посвящены вопросам математики, механики, геодезии, баллистики, фортификации. В трактате "Новая наука" (1537) он впервые рассматривает вопрос о траектории выпущенного снаряда, причём утверждает, что траектория эта на всём её протяжении есть кривая линия. До него же учили, что траектория снаряда состоит из двух прямых, соединённых кривой линией; тут же он показывает, что наибольшая дальность полёта соответствует углу в 45°; кроме того, в этой книге рассматриваются различные вопросы об измерении поверхности полей.

Вместе с вопросами артиллерии Тарталья занимался также и вопросами укрепления городов и фортификацией вообще и в сочинении «Quesiti et invenzioni diverse» (1546) он предлагает даже особую систему фронта; он пишет также о топографической съёмке с помощью буссоли и излагает историю открытия им решения кубических уравнений. В сочинениях «La travagliata invenzione» и «Ragionamenti sopra la Travagliata invenzione» (оба 1551 года) говорится о разных изобретениях автора, которые он приписывает себе, но все они уже изложены в 1550 г. в книге Кардано «De subtilitate» и принадлежат последнему.
Тарталья перевёл на итальянский язык "Начала" Евклида – это был первый перевод этой книги на современный язык.
Публикуя свои книги «Новая наука» (1537 г.) и «Проблемы и различные изобретения» (1546 г.), Тарталья писал, что в них «... новые изобретения, не краденые ни у Платона, ни у Плотина, ни у какого иного грека или латинянина, а полученные лишь искусством, измерением и разумом». Книги написаны в форме диалогов, на итальянском языке.
Наиболее обширное сочинение автора называется «Большой трактат о числах и мерах» (1556–1560); в нём подробно рассматриваются многие вопросы арифметики, алгебры и геометрии. В частности, в работе приводится формула, иногда именуемая формулой Тарталья или Герона – Тарталья, но открытая художником Пьеро делла Франческа в XV веке, с помощью которой можно найти объём произвольного тетраэдра через шесть расстояний между его вершинами. Это трёхмерный аналог формулы Герона для площади треугольника.
По своим человеческим качествам Тарталья был далеко не безупречен, во взаимоотношениях он был труден. Бомбелли писал, что Тарталья «по натуре своей был так склонен говорить только дурное, что даже хуля кого - либо считал, что даёт ему лестный отзыв». Говорили, что «он временами был так возбуждён, что казался умалишённым».

Умер Н. Тарталья 13 декабря 1557 года в Венеции. Обстоятельства его смерти неизвестны.
Тарталья вместе с Кардано и его учеником Феррари проложили главную тропу на пути, по которому в дальнейшем стала развиваться алгебра.
Заслуги Н. Тартальи в геометрии скромнее. Но и они весомы: как уже отмечалось, он перевел на итальянский сочинения Евклида и Архимеда — с тем, чтобы все желающие, включая таких же бедняков, каким он был сам, могли прочесть труды блестящих древнегреческих геометров.
Геометрические предпочтения самого Тартальи близки по духу идеям арабского математика Абу-ль-Вафы (940–998), который большое внимание уделял построениям с помощью линейки и циркуля постоянного раствора.
Валентин МАТЮХИН - обзор - 31 мая 2020

Джероламо Кардано (1501-1576)
Когда в 1541 году испанский король Карл V, император Священной Римской империи, триумфально въехал в завоеванный Милан, ректор коллегии врачей Кардано шел рядом с его каретой. В ответ на оказанную честь он предложил снабдить королевский экипаж специальной подвеской из двух валов, качение которых не выведет карету из горизонтального положения. В империи тогда дороги были плохие. Ныне такая система подвески называется карданом.

Эпоха Возрождения вошла в историю человечества не только прекрасными творениями художников, архитекторов и поэтов. Именно в это время были сделаны и многие научные открытия, которые превзошли все достижения античных и арабских ученых. Среди других гигантов мысли Возрождения незаслуженно теряется имя Джероламо Кардано (1501-1576).
Это знаменитый итальянский врач, математик, механик и философ. Его предшественником в эпохе был Леонардо да Винчи, а за ним следовал другой титан – Галилео Галилей. Если не принимать во внимание человеческие пороки, слабости, предрассудки, а судить по разносторонним знаниям и занятиям, по оставленным потомкам достижениям, Кардано стоит наравне с этими гениями. Но в историю науки он вошел с неоднозначной оценкой. Вокруг его имени все еще кипят шекспировские страсти. Кое-кто и теперь пишет о «клятвопреступлении Кардано».
Кардано родился внебрачным сыном известного миланского юриста Фацио Кардано, друга Леонардо да Винчи. Хорошо еще, отец до смерти успел оформить отношения с его матерью. Хотя сын уже был достаточно взрослым, окончил университет в Павии, стал доктором медицины. Вообще, Кардано считал себя в первую очередь врачом. Причем, не просто хорошим, а выдающимся, не хуже Гиппократа, Асклепия, Авиценны, Парацельса. Это было в его характере. В самом деле, большая часть жизни его врачебная практика шла успешно, он лечил знатных людей, имел высоких покровителей. Он стал профессором медицины в старейшем болонском университете, писал сочинения по медицине и фармацевтике. Он стал известен во всей Европе. Кардано в своих трудах описал приемы излечения до пяти тысяч трудно излечимых болезней. Он был хорошим диагностом.
Занятия медициной не поглощали Кардано всецело. Он стал известным изобретателем. Про известный карданный вал мы уже говорили. Это приспособление имеет честь носить имя Кардано, хотя использовалось еще в древнем Китае. Он же придумал кодовый замок. Известно, что он доказывал невозможность вечного двигателя, изучал оптические, электрические, магнитные явления.
Об утешении. Страница из трактата. De Consolatione, Hieronymi Cardani (1542)
Литературная карьера ученого тоже многогранна. Он издал более трёхста книг: по медицине, математике, по философии, астрологии, этике. Его энциклопедические трактаты «О тонких материях» и «О разнообразии вещей», в которых дано полное изложение состояния естественных наук, долгое время использовались в Европе как учебники. Особой популярностью пользовалась книга «Об утешении», переведенная на английский язык. Считается, что именно она вдохновила Шекспира на написание «Гамлета», а сам Гамлет произносит монолог «Быть или не быть», держа эту книгу в руках.
Увлекся Кардано и математикой. История формулы Кардано является одной из драматичных историй математики. Каждому школьнику известна формула вычисления корней квадратного уравнения. Такая же формула существует и для уравнения третьей степени, и именно она называется формулой Кардано. В истории математики она известна как первое серьезное достижение европейских математиков после многовекового застоя.

Формула Кардано для вычисления корней кубического уравнения
Подумаешь, решил уравнение, скажете вы. Но это с точки зрения современного человека. Во времена Кардано не было ни символической алгебры, ни даже отрицательных чисел. Эта формула вывела его в число первых математиков Европы. Но ... Именно она и присвоение ей имени Кардано многократно обсуждались в истории математики, как пример сомнительной чести. Дело в том, что эти методы, хотя и в частных случаях, знал другой итальянский математик Никколо Фонтана, по прозвищу «Тарталья». Кардано долгое время безуспешно пытался завладеть его секретом, но, в конце концов, ему это удалось. Он клятвенно заверил Тарталью не разглашать тайну даже после своей смерти, а также не опубликовать, пока сам Тарталья не сделает этого.
Кардано не только разобрался в методе Тартальи, но и развил его дальше. Поэтому он посчитал себя вправе опубликовать общую формулу. Таким образом, эта формула появилась впервые в знаменитом творении Кардано «Великое искусство» (Ars Magna, 1545 г.). Это его главный математический труд, крупный шаг в новую алгебру. Хотя Кардано и упомянул об авторстве Тартальи, с течением времени его имя забылось. Тарталья был взбешен, воспылал к Кардано ненавистью, долго на него нападал и жаловался. Но только заработал репутацию скандалиста и неудачника.
Излюбленным занятием Кардано была также астрология. Он составил гороскопы ста великих людей. Его гороскопами пользовались римские папы, за время его жизни их сменилось тринадцать. Хотя это не спасло его от суда инквизиции. В 1570 году он был призван в Рим и посажен в тюрьму на несколько месяцев. Возможно, ему зачлись гороскопы, и также наветы Тартальи. Последние годы жизни он провел в Риме под покровительством папы Григория XIII. Кардано скончался 21 сентября 1576 года. По известной легенде, эта дата значилась в составленном ученым для себя гороскопе, и он специально уморил себя, чтобы доказать свою демоническую силу.
Открытие метода решения кубических уравнений дало толчок к развитию всей математики. Но у математиков до сих пор нет единого мнения по вопросу: имел ли право Кардано публиковать формулы Тартальи, пускай даже только ради интересов науки?
отсюда
Статья создана по видеоматериалам творческих коллективов:





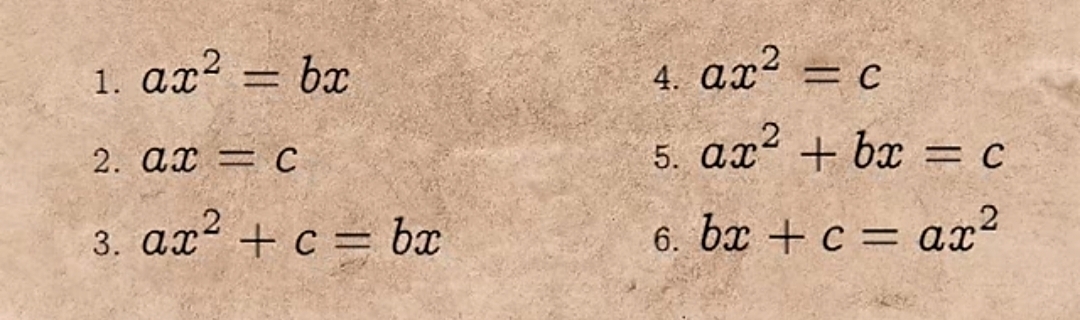


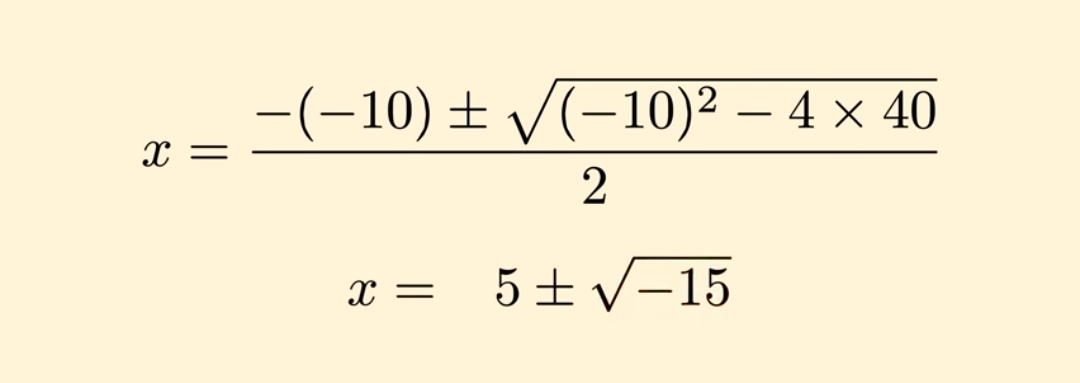
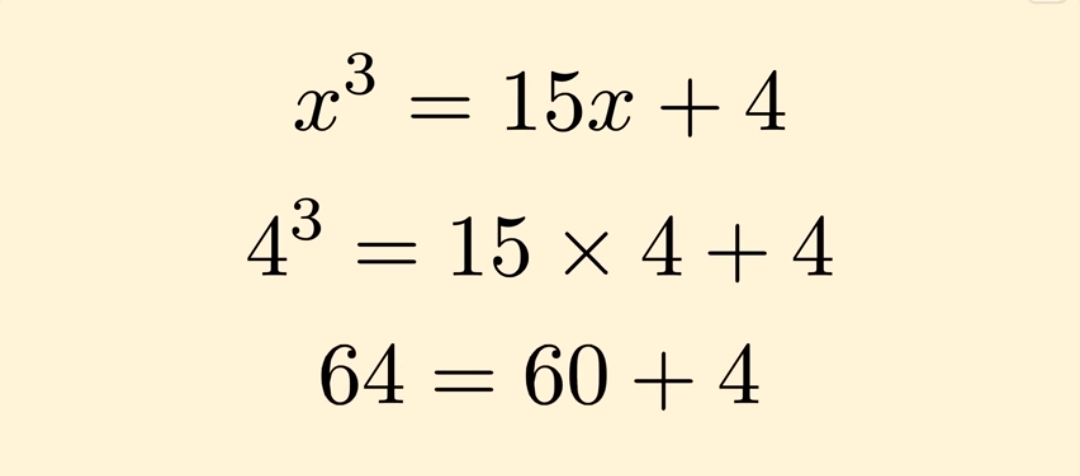
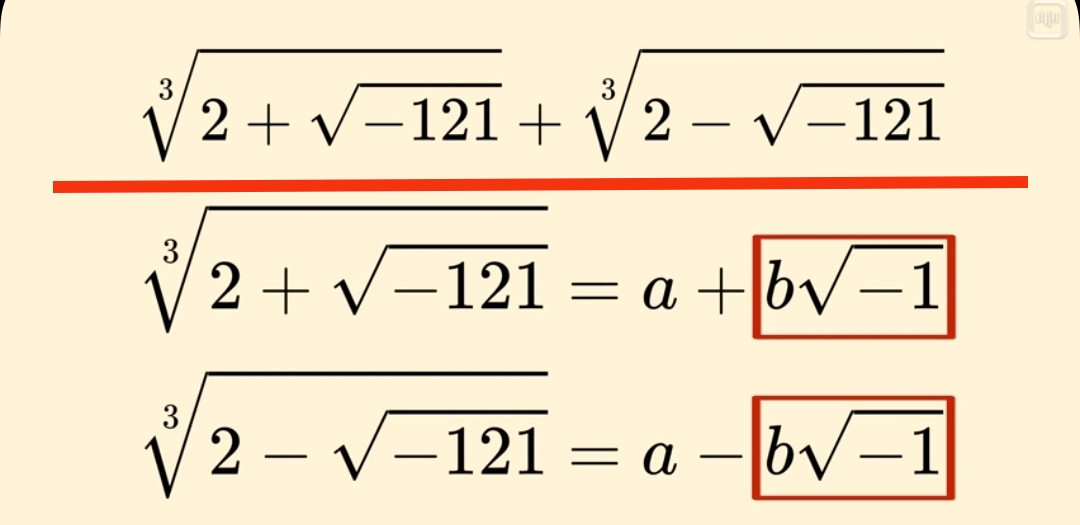
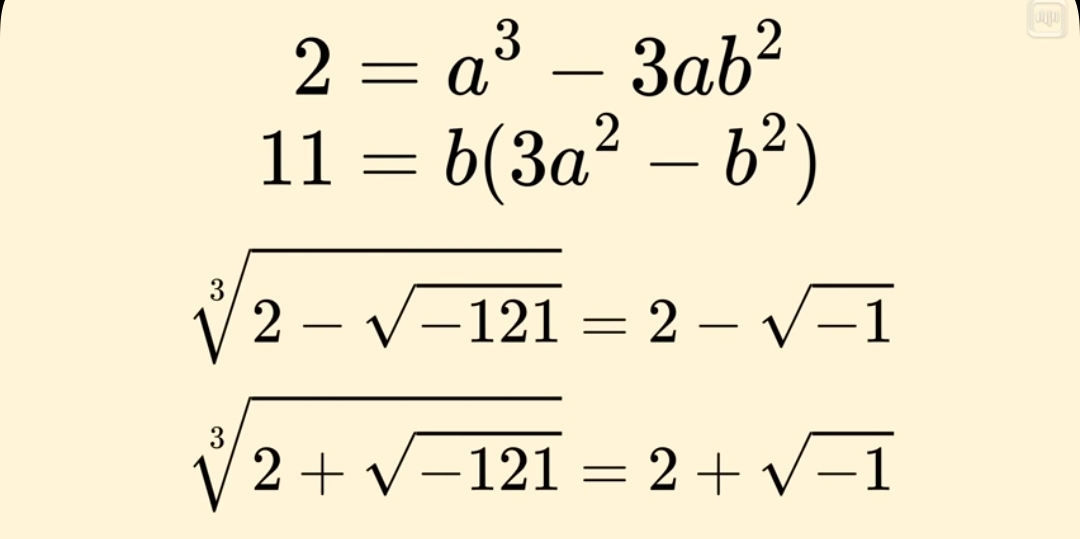 Это выглядит как настоящее чудо! То есть оказывается, что метод Кардано работает, но при этом нужно забыть про геометрическую интерпретацию уравнений и в некотором смысле формально работать с корнями из отрицательных чисел.
Это выглядит как настоящее чудо! То есть оказывается, что метод Кардано работает, но при этом нужно забыть про геометрическую интерпретацию уравнений и в некотором смысле формально работать с корнями из отрицательных чисел.






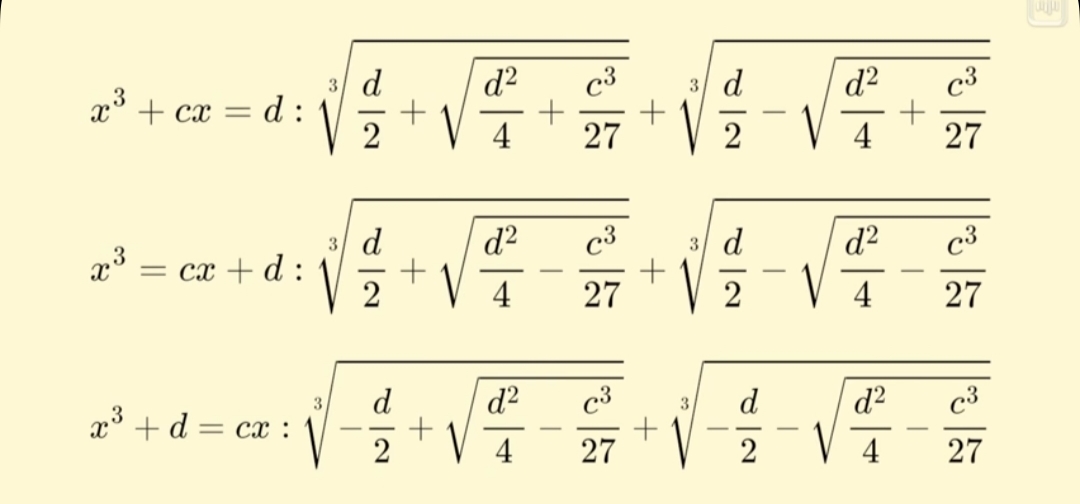



























Комментарии
расскажу кое-что из этой статьи детям на уроке, я учитель математики ))
https://dzen.ru/id/60fab3e3507049382858a3f4
Да ладно... Вы ж гуманитарий до мозга костей.
математика - наука гуманитарная.
.
Вам спасибо за отзыв. Добавил объема в виде видео, так что можно ещё и посмотреть.. )
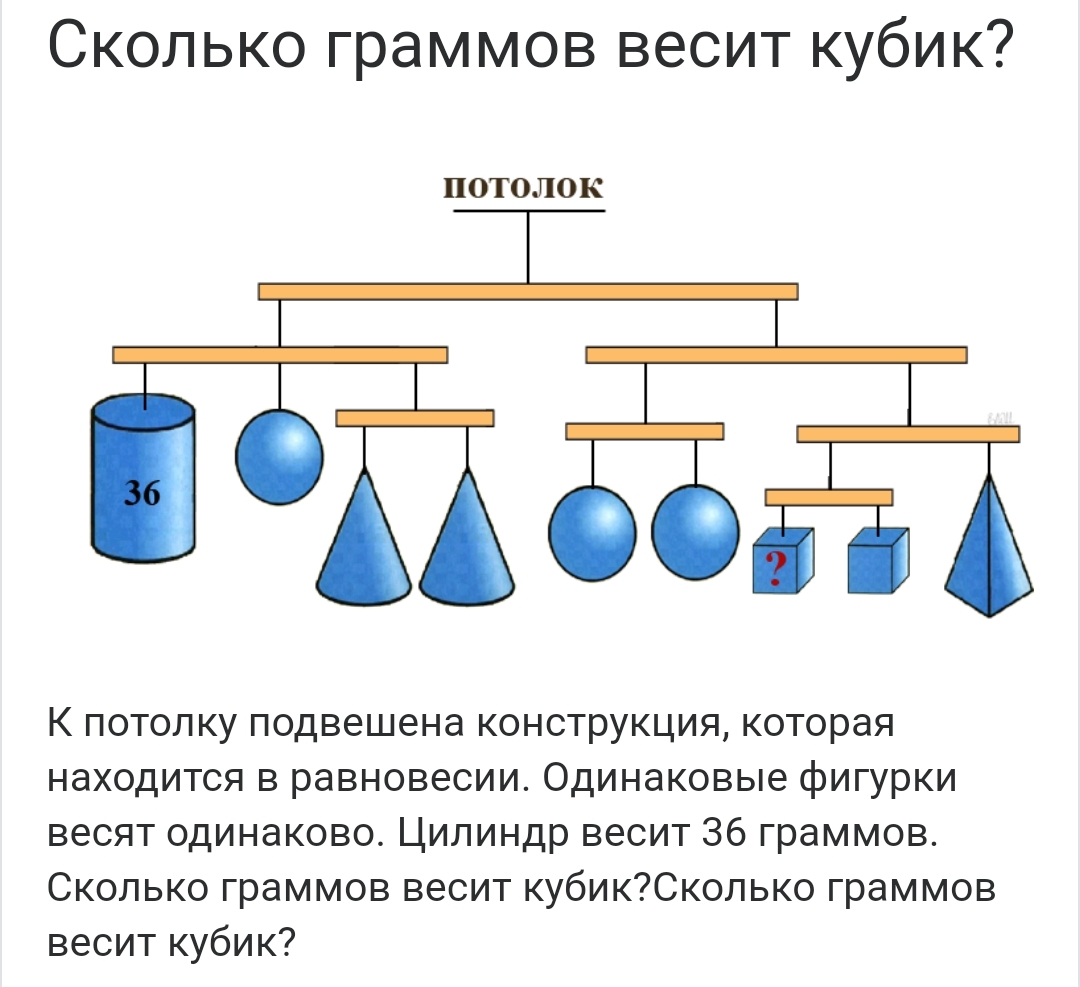
Кубик весит 12г.
Самое интересное следствие "изобретения" мнимой единицы - "отмена тригонометрии".
Указанные формулы превращают задачи тригонометрии просто в задачи на алгебраические преобразования.
"Синус и косинус - ошибки истории".
До сих пор не понимаю про что это ))
Но из видео следует, что в иррациональной плоскости синус и косинус между собой не различимы и имеют вид окружности, которая спираль в изометрии.. )
у меня получилось 12.
У меня тоже.. каким способом порешали? ))
72 +х=4х
а дальше всё пополам.
Я решал через средний вес
(72/3)/2
шарики с разных сторон перед вычислением аннигилировал.. ))
Хоспадя, как же тяжело людям до Декарта было жыдь.
Помню в институте нам преподавали "теорию функции комплексного переменного" и "уравнения математической физики". Запомнилось только, что это какая-то невероятная абстракция, которую вообще непонятно где можно применить. Вычеты какие-то. Потом ни разу не пригодилось.
Я сломался еще на косинусах и синусах..
Перспективный чат детектед! Сим повелеваю - внести запись в реестр самых обсуждаемых за последние 4 часа.
Кубик=12гр
По задачке в конце авторского комментария - кубик весит 12 граммов. (ну при условии, что система подвеса никакого значения не имеет)
Как не имеет? ))
Очень даже имеет. Без системы подвеса задача была бы не решаема.
Как решили?
Он совершенно справедливо имеет в виду, что в условии задачи должно быть прописано игнорирование веса элементов конструкции самого подвеса. Но этого не сделано, поэтому человек сделал допущение, упростив задачу, о чём и написал.
С таким допущением решение элементарно: линейное уравнение с одной переменной. Без него - задача нерешаема, если опять же не сделать допущения о пропорциях балок подвеса и размерах креплений (нитей).
Нет конечно, задача имеет упрощённый вид.. Сама система подвесов, кмк, это достаточно оригинальное и логический понятное выражение смысла знака «равенство». В задаче их семь.
Это, кмк, хорошая отсылка к пониманию комплексных чисел, где мнимая часть в данном случае может быть представлена в виде множества знаков равенства.
Это если не учитывать разницу длин элементов системы по разные стороны верхней балки. О чём я и писал.
Если учитывать, решение, кстати, может существовать лишь в ограниченном массиве пропорций длин элементов системы)) Умозрительно, лишь в том, где пропорции приводят к равенству веса элементов системы справа и слева. Если конструкция подвеса (без грузов) не будет равновесной, то при заданных системе грузов и условии задачи решения (с помощью комплексных чисел или без них) не существует.
Поэтому, возвращаясь к исходному комменту ветки ("при условии, что система подвеса никакого значения не имеет") я наблюдаю компромисс: условие, чтобы система подвеса сама по себе была равновесной - существенно, остальное - нет.
Умозрительно без потолка задача вообще за гранью понимания и здравой логики находится. ))
Если система подвеса будет равновесной, то её уже можно исключить из решения путем аннигиляции равнозначных масс. )
через систему уравнений: 72 + х = 4х и х =2у, х - шарик, у - кубик.
там кстати еще пирамидка справа равна по весу шарику.
Что-то так и не понял, а кто крестик-то вытянул? Где решение кубического уравнения с корнем х=4 методом, отличным от перебора?
Комплексные числа стоят особняком, потому что они, в отличие от всех остальных, не одномерные и их нельзя указать в воде точки на координатной прямой.
А вся эта "иерархия чисел" сейчас никакого практического смысла не имеет, любое число в ЭВМ представляется в виде десятичной дроби. Поэтому для компа нет никакой разницы, что перед ним - рациональная дробь или вещественный корень, или вообще число пи.
Ну если позанудствовать немного, то в ЭВМ всё представляется в виде 0 и 1, и все остальные числа она представляет в виде множеств из этих двух чисел.. поэтому люди и заморочились созданием квантового компьютера, потому как он проводит вычисления, оперируя кубическими множествами гораздо лучше, чем это делает обычный компуктер
Иерархия чисел, вероятно, возникла с появлением теории множеств, которая классифицирует цифры по тем или иным свойствам.
Множества входят одно в другое. Комплексное число само из себя представляет множество. Так что комплексное множество - это множество множеств. И развернуто оно в иной координатной плоскости выражения числа, т.е. в объеме.
Комплексные числа подразделяются на алгебраические и трансцендентные, где каждое действительное трансцендентное является иррациональным, а каждое рациональное число — действительным алгебраическим... что бы это не значило. )
По решению, если честно, сам не до конца понял.. В конце статьи есть видео от vert dider, там чуть больше информации по решению..
Иерархия чисек еще в древности появилась, и тогда она имела смысл, потому что не было компьютеров и те же простые дроби не переводились в десятичные. А сейчас нет никакого смысла запоминать, чем вещественное число отличается от рационального, с практической точки зрения оно ничем не отличается. По сути сейчас числа классифицируются так:
1. Целые
2. Конечные десятичные дроби
3. Бесконечные десятичные дроби
Как по вашей классификации можно представить корень из минус единицы: целое ли это число или бесконечная десятичная дробь?
Корень из минус единицы физического смысла не имеет и на числовой координатной оси его изобразить невозможно. Это фантом, созданный исключительно для удобства некоторых расчетов.
Ну собственно про это и статья.. древние говорили тоже самое относительно отрицательных чисел и всяких квадратов из них.
Ну не совсем так.. вполне нормально изображается в своей координатной плоскости.
Этот фантом стал неотъемлемой частью физики.
Отрицательные числа имеют смысл долга. Умножение на -1 имеет смысл смены знака (актив становится пассивом, и наоборот). Все остальное следует из этого. Умножение на отрицательное число - сначала идет умножение на -1, что меняет знак, а потом умножение на положительное число обычным образом.
В координатной плоскости i не отображается, отображаются коэффициенты при нем.
Про смысл иррационального числа будет статья чуть позже. И про координатную плоскость i, тоже есть некоторые соображения, но пока не могу их сформулировать внятно..
Есть хороший документальный фильм на эту тему - " пять чисел, которые изменили мир"...
Если не ошибся вес кубика 72/6=12
Это i имеет конкретный так сказать смысл и вполне возникает после второго измерения - площади.
Конкретно площадь - ну квадрат.
А вот масса - двумерна, но она не совсем площадь, масса - поверхность, так как гравитационная её составляющая - гравитационная масса - имеет НАПРАВЛЕНИЕ!.
И мы имеем отличие площади от поверхности - у поверхности есть верх и низ (кроме собственно размера площади), а для площади - направление фиолетово!
Вот там-то и зарылась нам неведомая i - оказывается, это корень квадратный из минус единицы!
И с зарядом - та же петрушка! Только там этих i должно быть больше одной...
Спасибо!
Именно поэтому математика пришла в тупик. Отсоединилась от физики.
Спасибо! Весьма забавно. И пришлось вспомнить уже забытое.