Я не математик, и вполне возможно что данный материал давно уже известен. Если так - дайте знать.
Когда-то давно, ещё в юности, интересовался разным, необычным. Были последние годы существования Союза и начала РФ, когда к нам хлынули неведанные ранее в Союзе вещи от религиозных проповедников, мистиков типа Рерихов, Блаватской, а также был потоп от всяких пседвонаук и религий до заряжания тазиков по государственному ТВ. (Может кто помнит таких как Алан Чумак или дающего всей стране "установку на добро" Кашпировского.)
Вот и меня привлекла такая вещь как астрология. Носился с ней пока не усвоил первый закон астролога: Звёзды правят дураками, а умный сам правит своими звёздами. После чего с астрологией завязал.
Но до того как с ней расстаться случилось мне создать одну вещь, о которой хочу рассказать.
Сама астрология, на мой взгляд, это что-то вроде религиозного культа, где адепты верят что характер человека и его судьба зависят от расположения небесных тел на небесной сфере и их отношения друг к другу. Угловые расстояния между небесными телами играют ключевую роль в астрологии при составление натальной карты (гороскопа рождения). Сами угловые соотношения называются - аспекты. Это следующие: 0, 180, 120, 90, 72, 60, 45, 40 ... и так далее. Положения планет повторяются и на это уходят месяцы, годы, столетия. Всё это — циклы. Но, есть и большие циклы, которые я взял у Блаватской: день Брамы (4,32 миллиарда лет), век Брамы (3,1104⋅1014, или 311 триллионов 40 миллиардов лет), и другие. Были ещё циклы - деление кальпы на юги:
Сатья-юга (Крита-юга): 1 728 000
Трета-юга: 1 296 000 земных лет
Двапара-юга: 864 000 земных лет
Кали-юга: 432 000 земных лет.
А также - Восемь адов в буддийской философии:
Санджива-нарака (Sañjīva) — ад оживления. Пребывание в этом аду занимает 162⋅1010 лет.
Каласутра-нарака (Kālasūtra) — ад чёрных сечений. Пребывание в этом аду занимает 1296⋅1010 лет.
Сангхата-нарака (Saṃghāta IAST) — сокрушающий ад. Пребывание в этом аду занимает 10 368⋅1010 лет.
Раурава-нарака(Raurava) — ад воплей. Жизнь в этом аду составляет 82 944⋅1010 лет.
Махараурава-нарака (Mahāraurava) — ад великих воплей. Жизнь в этом аду составляет 663 552⋅1010 лет.
Тапана-нарака (Tapana) — жаркий ад. Жизнь в этом аду составляет 5 308 416⋅1010 лет.
Пратапана-нарака(Pratāpana) — ад великого жара. Пребывание в этом аду занимает 42 467 328⋅1010 лет.
Авичи-нарака (Avīci) — непрекращающийся ад. Пребывание в этом аду занимает 339 738 624⋅1010 лет, до конца антаракальпы.
И я задался вопросом: А нет ли здесь связи или закономерности которая позволяла бы выводить все эти числа?
Ведь это — циклы. Значит должно быть что-то — какой-то принцип или закономерность с помощью которой можно было бы вывести их все.
Меня интересовали только числа, не философия.
Такой числовой ряд получить можно.
И в этом ряду есть все, или почти все, упомянутые числа но - без нулей. То есть если число к примеру 864 000 (Двапара-юга), то в числовом ряду есть - 864. Тоже самое и по остальным «-югам», есть и 1728 (Сатья), 1296 (Трета), 432 (Кали).
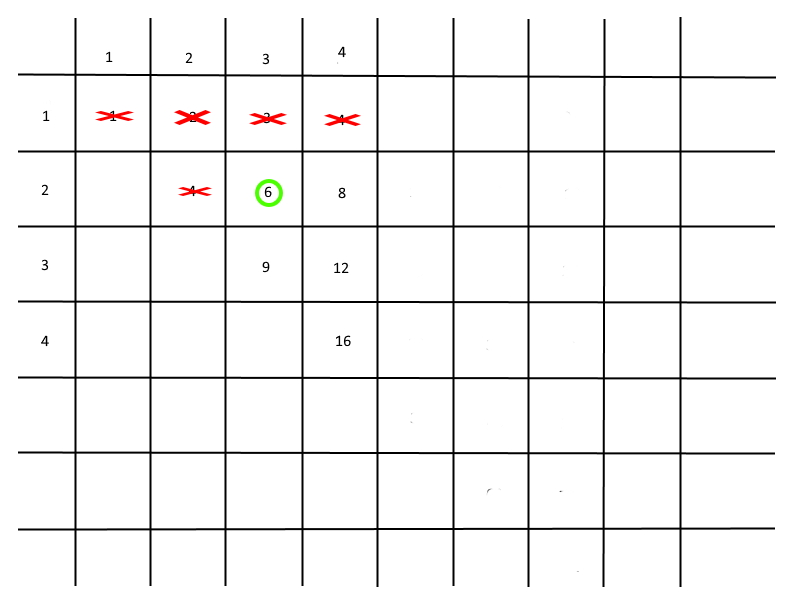
Как это делается? Для начала нужно построить матрицу 3х3. Берём три числа: 1, 2, 3. Откладываем их по вертикали и по горизонтали - базовые ряды.
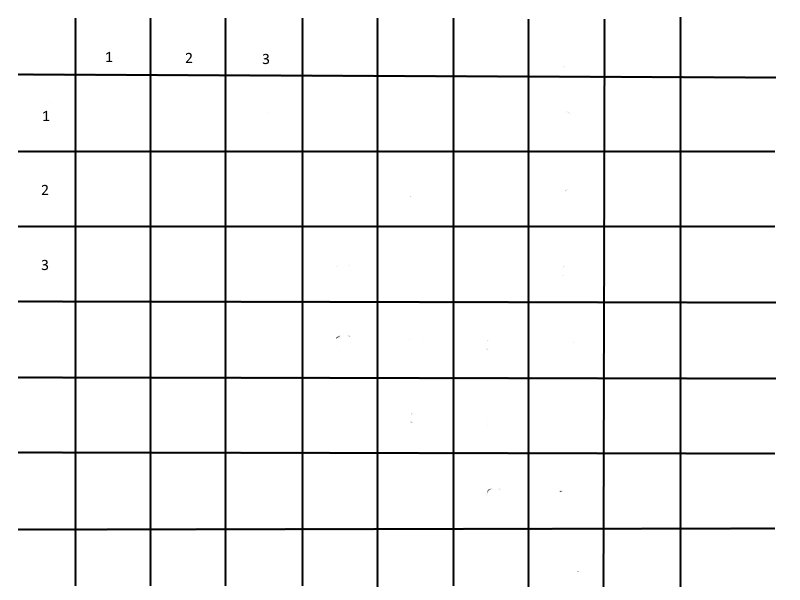
(рис 1)
Далее, умножаем числа в базовых рядах друг на дружку. Получаем следующее.
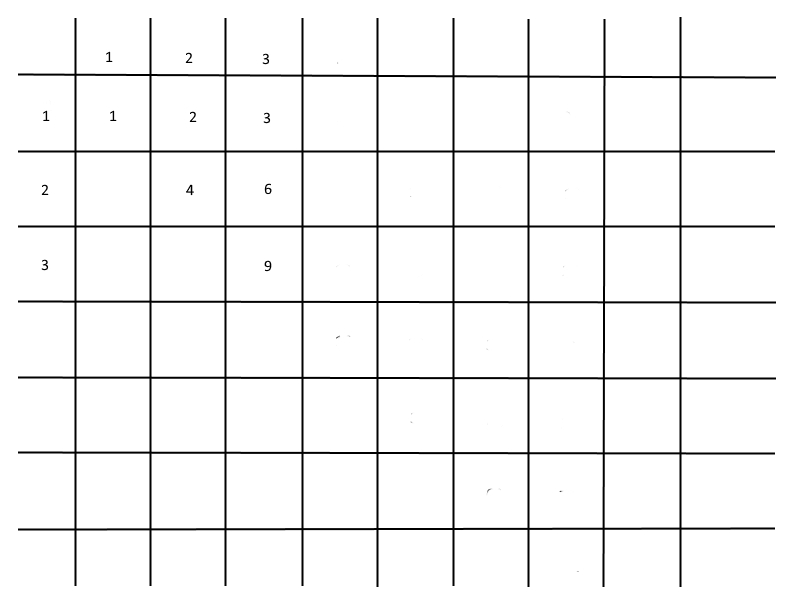
(рис 2)
Из полученного массива чисел вычёркиваем те, которые уже есть в базовых рядах.
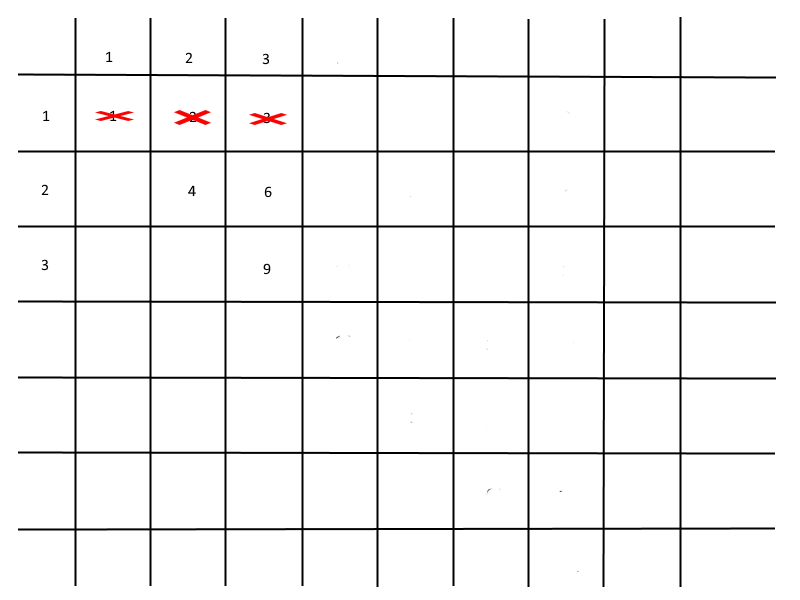
(рис 3)
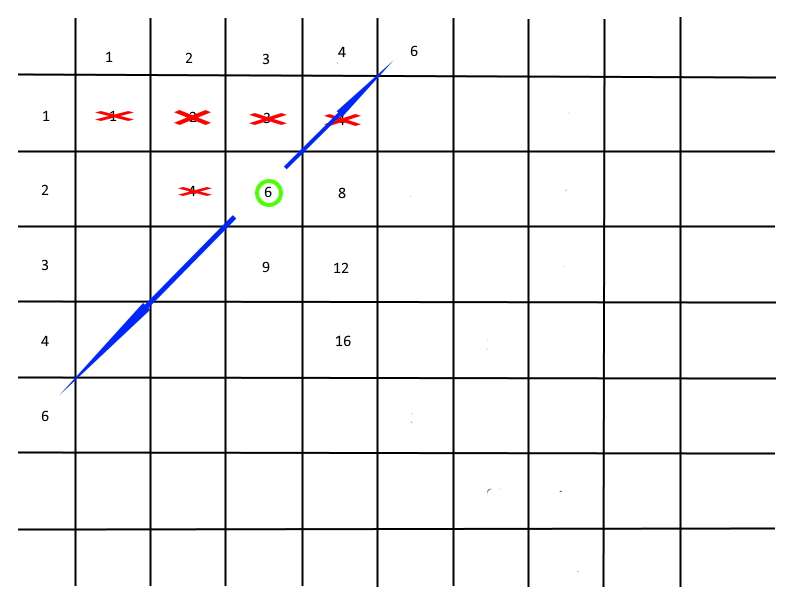
Из тех что остались не вычеркнутыми берём наименьшее и дополняем базовые вертикальный и горизонтальный ряды.
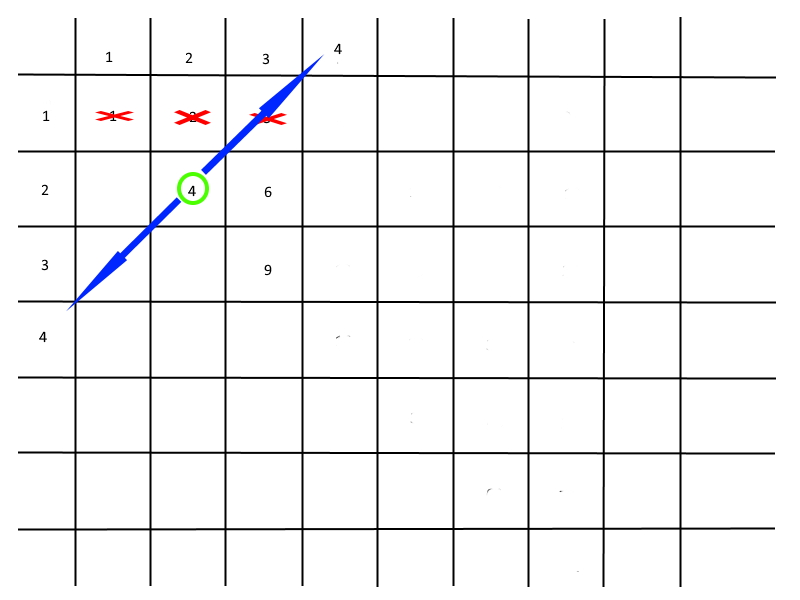
(рис 4)
И снова - умножение, вычёркивание, поиск в оставшемся наименьшего, дополнение наименьшим из оставшихся числом базовых рядов.
(Рис 5)
(Рис 6)
Вот и весь алгоритм.
Получается следующая последовательность чисел в базовых рядах: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 32, 36, 48, 54, 64, 72, 81, 96, 108, 128, 144, 162, 192, 216, 243, 256, 288, 324, 384, 432, 486, 576, 648, 729, 768, 864, 972, 1024, 1152, 1296, 1458, 1532, 1728, 1944, 2048, 2304, 2592, 2916, 3072, 3456, 3888, 4096, 4608, 5184, 5832, 6144, 6912, 7776, 8192, 8748, 9216, ....
Когда-то расчитал вручную ряд до первых семизначных. Но рутины с этим было много и времени это занимало уйму.. Здесь даю только принцип развёртывания ряда, и первые числа в нём. (Здесь, и ниже в этой статье, называю его «гармоничным числовым рядом» только чтобы избежать путаницы с чем-либо другим.)
Получается следующее (базовые ряды выделил жёлтым цветом):
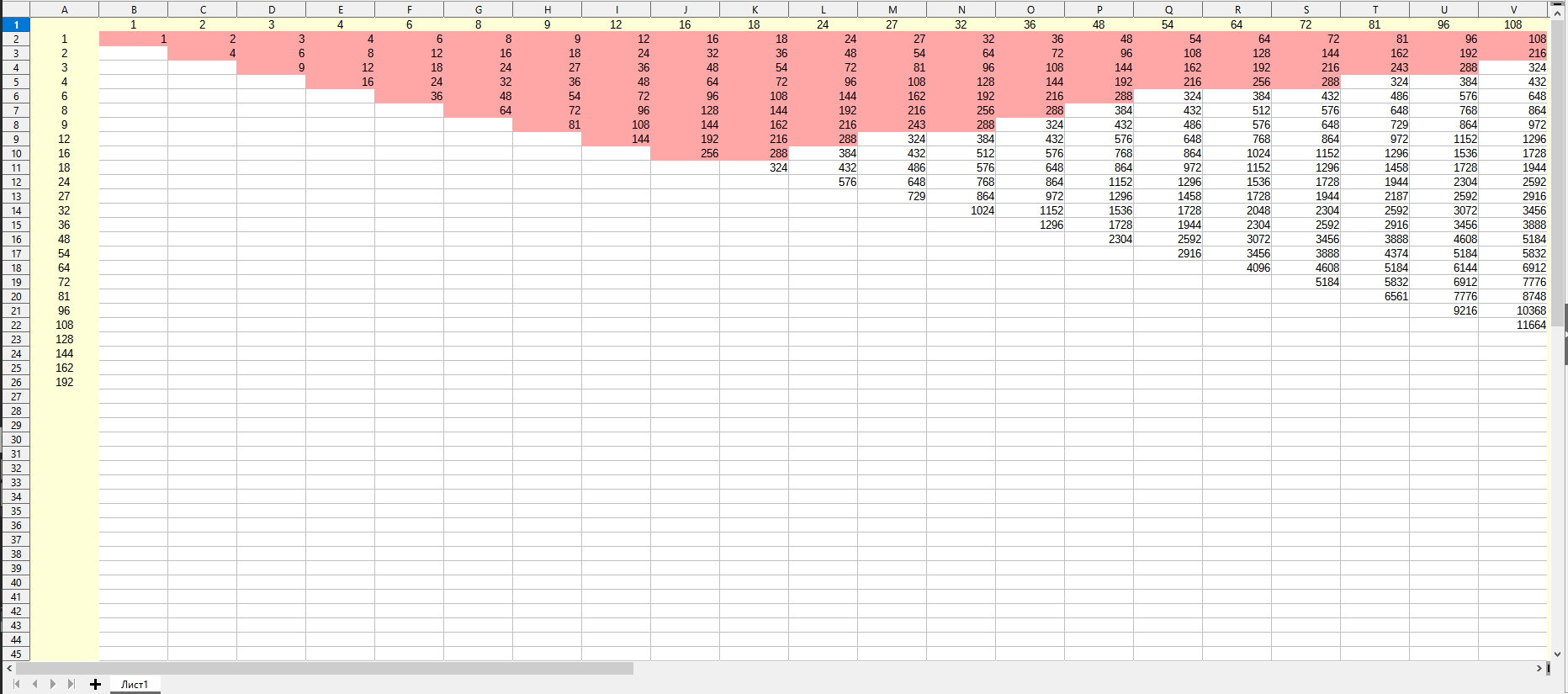
(Рис 7)
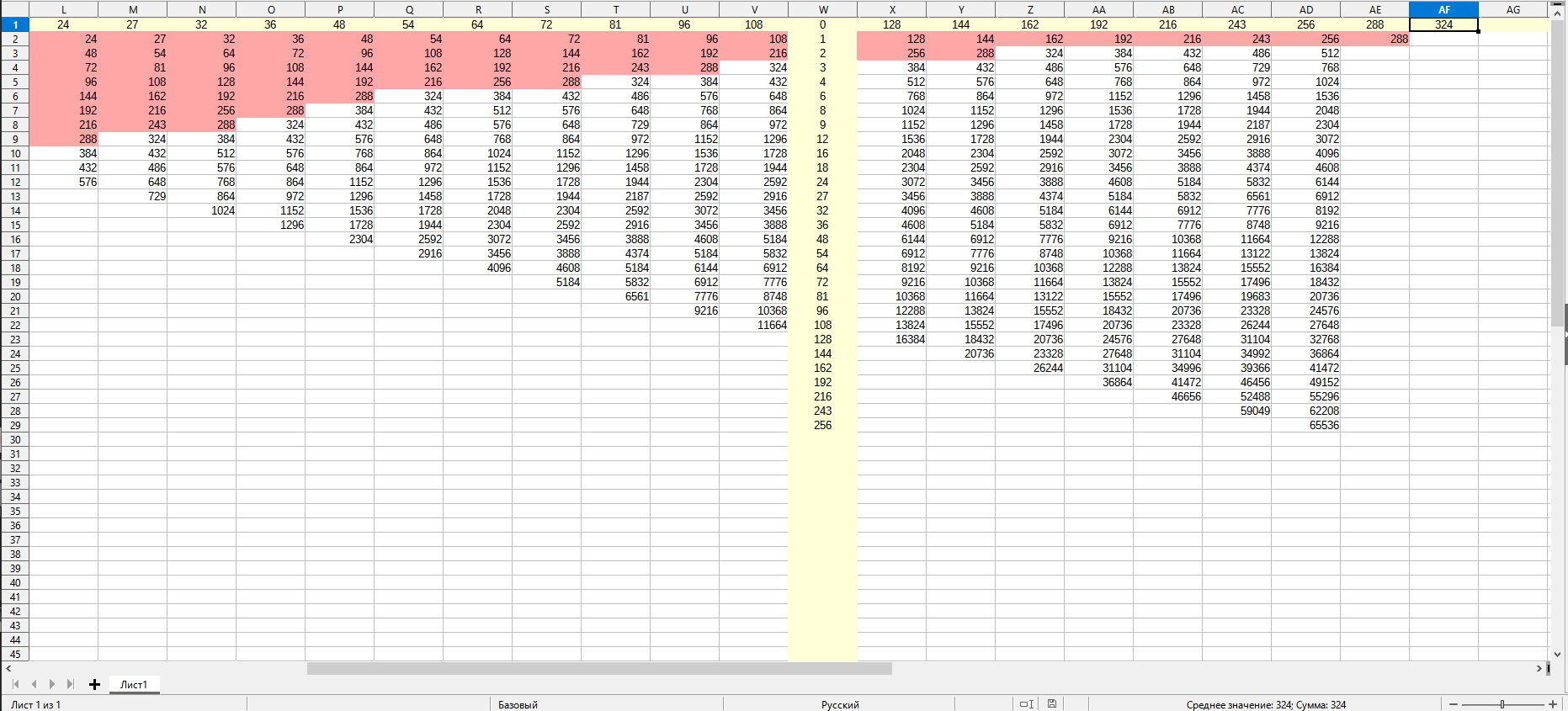
(Рис 8)
Можно сделать и другую вещь - деление. Посмотреть - какие будут результаты деления если начать базовый ряд как 1, 1/2, 1/3? То есть если при вычислении базовых рядов производилось умножение, то тоже самое можно сделать и с делением. Но можно взять и готовые вычисленные базовые ряды и посмотреть соотношения в имеющихся в них числах. Игрался когда-то и так и так. Деление вручную — то ещё удовольствие. Умножать проще.
Например выписывал их как дано ниже, и смотрел на соотношения:
1, 1.024, 1.08, 1.152, 1.2, 1.28, 1.296, 1.44, 1.458, 1.532, 1.6, 1.62, 1.728, 1.8, 1.92, 1.944,
2, 2.048, 2.16, 2.304, 2.4, 2.43, 2.56, 2.592, 2.7, 2.88,
3, 3.072, 3.2, 3.24, 3.456, 3.6, 3.84, 3.888,
4, 4.096, 4.32, 4.608, 4.8, 4.86, 5.184, 5.4, 5.76, 5.832,
6, 6.144, 6.4, 6.48, 6.912, 7.2, 7.29, 7.68, 7.776,
8, 8.1, 8.192, 8.64, 8.748,
9, 9.216, 9.6, 9.72,
Если в каждом из семи горизонтальных рядов брать любое число и смотреть на его соотношение с другими, то у некоторых пар получаются соотношения такие же как у нот в натуральном звукоряде. Здесь имеется в виду музыкальный строй с нотой Ля первой октавы в 432 гц.
http://ookiimomolasai.blogspot.com/2014/05/musica-y-geometria.html
У кого есть желание могут сами сделать простейшие вычисления. Например: 9.216/9.6=0.96, 8.1/8.192=0,98876953125, 8.192/8.1=16/15, 8.748/8.1=1.08, 6.4/6.48=0,9876543209876543, 5.4/6.4=34.56, 6/5.4=1,111111111111111, 6.48/5.4=1.2, 6.48/7.29=0,8888888888888889, …
Чем-то перекликается с тем что изложенно здесь: https://reel-2-reel.livejournal.com/3876.html
Какая ещё есть особенность?
Несколько лет назад читал о том, что хотели использовать в компьютерах наряду с обычной двоичной системой ту же систему но не по основанию двойки, а на основе ряда Фибоначчи. Можно ли использовать для этого этот числовой ряд? Запрета на это нет, но нужно ли — пусть решают те кто в теме.
Гармоничный ряд позволяет записать одно и тоже число несколькими вариантами.
В чём отличие и возможное преимущество?
Двоичная система, общепринятая.
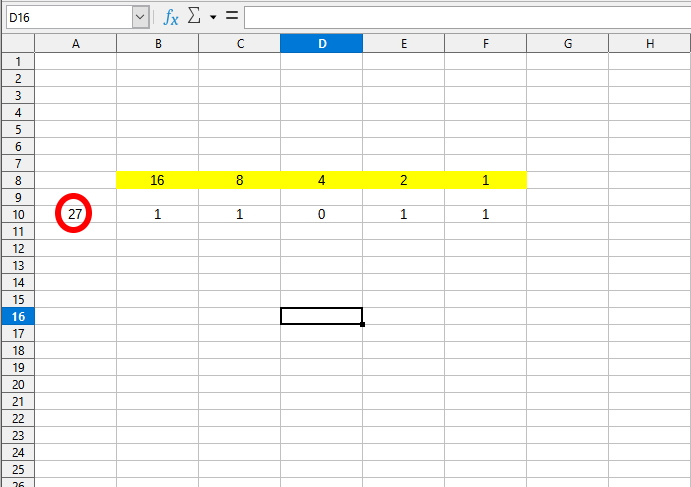
(рис 9).
В общепринятой двоичной системе с основанием по степени двойки любое число имеет только один вариант написания. (Для примера взято число «27»).
Двоичная система на основе ряда Фибоначчи. Если взять ряд Фибоначчи, то тоже самое число «27» имеет уже четыре варианта написания.
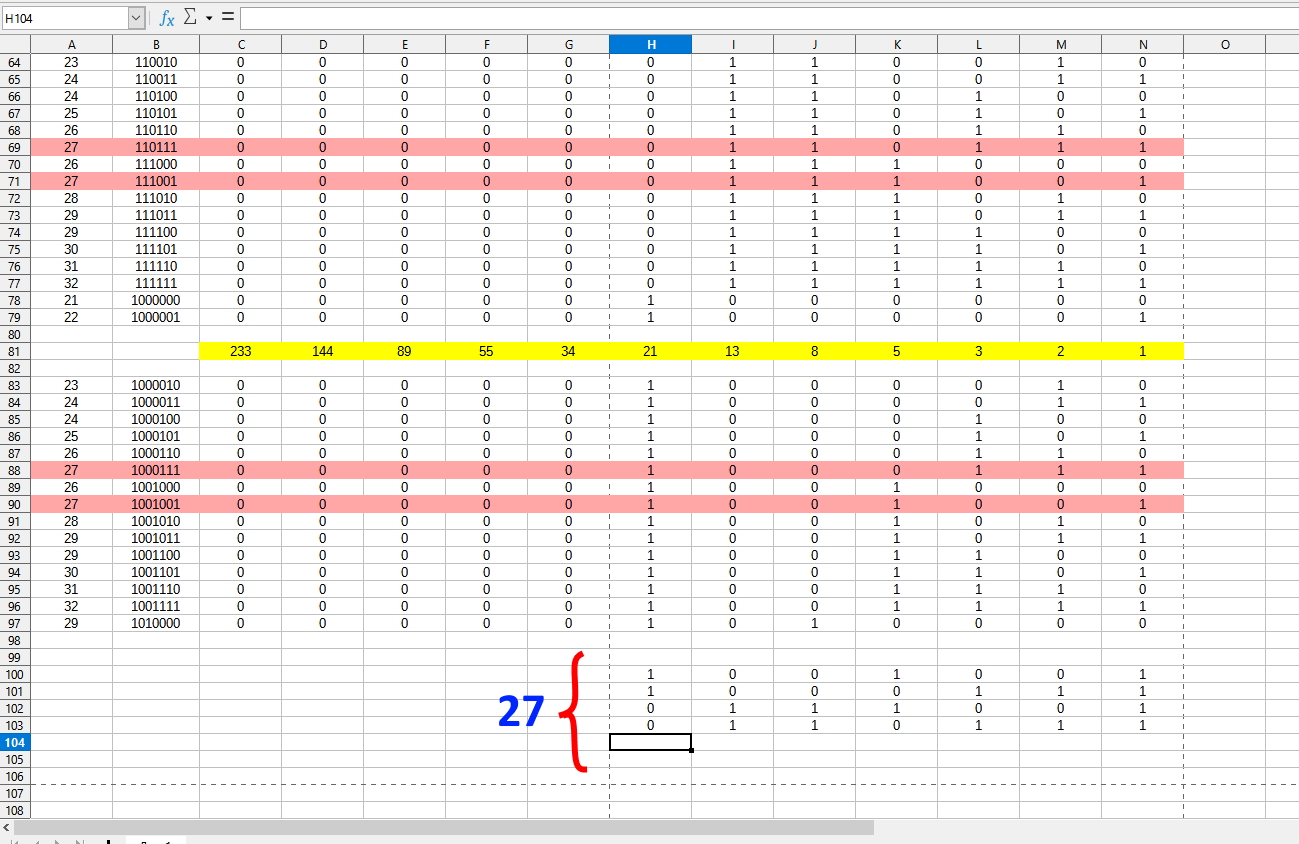
(рис 10)
Гармоничный числовой ряд.
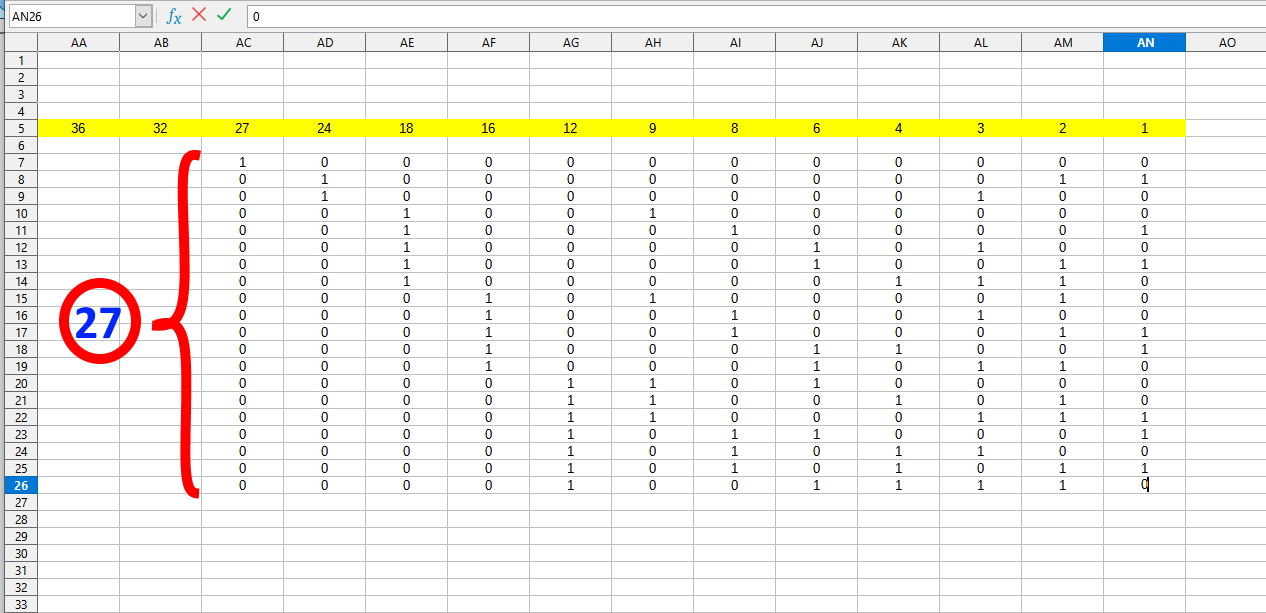
(рис 11)
При использовании гармоничного числового ряда, число «27» можно записать двадцатью различными вариантами: 100000000000, 010000000011, 010000000100, 001001000000, 001000100001, 001000010100, 001000010011, 001000001110, 000101000010, 000100100100, 000100100011, 000100011001, 000100010110, 000011010000, 000011001010, 00001100111, 000010110001, 000010101100, 000010101011, 000010011110.
И каждый вариант даст при обратном преобразовании именно 27.
FreeWind





Комментарии
Собственно все что следует знать об этих изобретателях адовых вселенных, выражено в этой цифре 1010 лет
Даже не знаю, как описать ограниченность человека, которому надо загнать человека в ад на подобные сроки
Думаю что Вселенная бесконечна. Но не уверен.
По слухам, индийские ученые вывели формулу, по которой можно рассчитать площадь слона.
Со слоном хоть количество шампуня можно прикинуть, если оного помыть приспичит. А с этими числовыми системами что делать?
Вот и я не знаю. Но алгоритм вывел. Может кому и пригодится.
Есть такое ответвление, как нумерология. Вот любят они циферки.
В математике всё имеет прикладное значение, по этому критерию можно разделять.
К примеру те же числа Фибоначчи возникли из конкретной прикладной задачи - как размножение.
Если есть интерес, то ключевое слово для поиска "нумерология" ;)
В целом, в США не любят математику, там любят цифры - по этому у них конспирология и прочее как раз базирует свои концепты на поле множества операций над числом/цифрами, хотя зачастую занимаются методом подгонки под ожидание, но развлечение такое крайне распространённое.
Так что, вопрос "к математикам" тут не сильно уместен, тут любой умеющий складывать/умножать/вычитать и фанатеющий от простых операций над числами (иногда мне кажется, что это некоторый фетиш) может посоветовать что-то с этим сделать (хотя я реально не вижу прикладного применения)
Тем более прикладного не видел и я. Сам алгоритм был найден очень давно. Единственное где это могло бы быть пригодным так это - шифрование. Но боюсь что профессиональные криптографы лопнут от смеха.
Учитывая текущее веянье моды, то можешь криптовалюту на этом запустить xD
Беда, коль пироги начнет печи сапожник,
А сапоги тачать пирожник,
И дело не пойдет на лад.
Да и примечено стократ,
Что кто за ремесло чужое браться любит,
Тот завсегда других упрямей и вздорней:
Он лучше дело всё погубит,
И рад скорей
Посмешищем стать света,
Чем у честных и знающих людей
Спросить иль выслушать разумного совета.(с)
Не вник, но напоминает рассказ Пелевина "Числа".
1) Если отбросить всё что про эзотерику, то останется алгоритм построения числового ряда. Ряд чем-то напоминает ряд Фибоначчи, но стоится по иному алгоритму.
2) Ряд показывает числовые значения гармоник, и по числам есть совпадения с гармониками музыкального строя в 432 Гц. Также ряд позволяет видеть соотношения этих гармоник.
Когда-то, когда ещё смотрел свойства получаемого в результате алгоритма числового ряда то взял книгу по настройке роялей, и поразился совпадениям.
3) Этот ряд можно было бы использовать и для шифровки текстов или данных, с повышенной хаотичностью зашифрованного. Повышенная хаотичность, это когда каждая буква, каждый знак и даже пробел между словами могут быть записаны более чем двумя десятками вариантов. При этом и отправителю и получателю для шифрования и расшифровывания не нужно ничего кроме ручки и бумаги. Но это, чисто умствование. Я не являюсь криптологом, поэтому рассказывать о том насколько это хорошо не возьмусь. Предположение что это можно использовать для шифровки я высказать могу, что и сделал. Но не более. И это единственное где я могу предположить практическое применение созданного мною алгоритма.
Если кто-то найдёт этому действительно полезное применение на практике, а не как у меня - чисто умственная спекуляция - хорошо. Мне самому было бы интересно узнать это.
А хотите прикол. Двенадцатеричная система счисления появилась как счет большим пальцем костяшек оставшихся четырех пальцев.
P.S.
Две ошибки выявлено в таблице на рис №8
(первая цифра - столбец, вторая - строка):
АВх25 216х162=34992 а не 34996.
АСх26 243х192=46656 а не 46456.
Небольшое уточнение рядов.
При подготовке статьи упустил два числа. Исправляю.