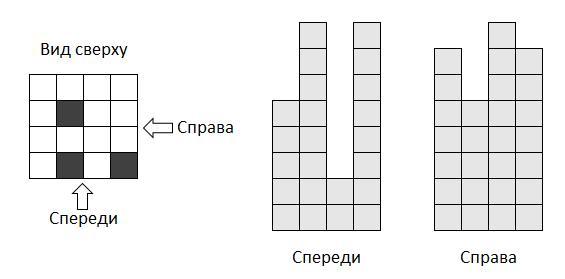
Никита взял доску 4×4 и на каждую клетку поставил столбик из кубиков. На две клетки по 1 кубику, на две клетки по 2 кубика, на две клетки по 3 кубика, …, на две клетки по 8 кубиков. Потом он нарисовал, как выглядит конструкция спереди и справа (если перед столбиком из 8 кубиков стоит столбик из 5, то Никита нарисует столбик из 8 кубиков). Сколько в сумме кубиков он поставил на 3 выделенные клетки?
Комментарии
Б3 - 8
Согласен! по 8 штук в рядах 2 и 4 по X и в 3 по Y / поскольку их всего 2 значения то (2X,3Y) 8
А то, что Спереди правый столбец должен равняться Справа левый столбец !? (просто потому, что это один и тот же столбец кубиков)
Никого не смущает ?
вот - вот, то же смотрю - глазам не верю....четвертый столбец в виде спереди и первый столбец в виде справа - это, если верить правилам черчения, один и тот же столбец....по крайней мере должен быть ... так что начинать надо с того, кто составлял задание....
То не "столбец", то проекция 4х столбцов, включая первый правый спереди.
на выделенных клетках 21 кубик 6+7+8
восьмерки определяются сразу, а для шестерок и семерок место остаётся 4 места в первом и четвёртом ряду, причём семерка должна быть в обоих
21 тоже. Причем не важно какой клетке внизу 6 и 7
Да, 21. 8-Ки ставятся однозначно. И две неразличимые комбинации 6+7, вместе 21
8-ки точно на своих местах, а 1 и 2 точно находятся на указанной линии, но в любом порядке , т е или 2 2 1 1, или 2 1 1 2, и т.д. Дальше логики, дающей четкое понимание сколько именно находится в клетке, например 5 или 3 я не нашел. Дальше идут одни диапазоны из серии, меньше или равно 5 и меньше или равно 7.
Прочел комментарии остальных: да .. 21 получается.
PS. Про Катю: В классе 14 человек, у Кати 13 одноклассников.
13 человек в классе и 12 одноклассников
21. Обозначим клетки как на шахматной доске (уменьшенной), a b c d по горизонтали 1 2 3 4 по вертикали. Восемь кубиков определяются однозначно b3 d3. Соответственно семь и шесть кубиков прячутся по этим же вертикалям b и d. Их можно разместить либо семерки b1 d4 шестерки b4 d1, либо шестерки b1 d4 семерки b4 d1. В любом случае на выделенные клетки выпадет одна восьмерка, одна семерка и одна шестерка.
Спасибо!
и ещё
либо семерки b1 d1 шестерки b4 d4, либо шестерки b1 d1 семерки b4 d4
Нет. Из вида справа следует, что семерки располагаются в двух горизонталях первой и четвертой.
ну да, поспешил. поменял цифры, а надо было литеры. так
либо семерки b1 b4 шестерки d1 d4, либо шестерки b1 b4 семерки d1 d4
Да, так можно. Но на результат не повлияет :)
Я решил методом исключения. b2 и d2 -- восемь, это понятно. На c1-c4 два поля заняты одним кубиком, а два поля -- двумя. На a2 - пять кубиков, на оставшихся свободных полях a1-a4 и a2-d2 -- два поля с тремя, два поля с четырьмя и одно поле с пятью кубиками. Остаётся четыре поля b1, d1, b4 и d4. На них два раза по шесть и два раза по семь кубиков (остальные уже распределены), причём семь кубиков не могут быть на одной горизонтальной линии.
То есть на трёх клетках будет 6, 7 и 8 кубиков, итого 21.
бред. по условию задачи должно быть занято 8 полей из 16. что стоит на выделеных вообще не поятно.
Вообще то заняты все 16 клеток
Большого желания спорить нет, математик из меня так себе, но:
Иттого: 2(по одному)+ 2(по три)+ 2(по два)+ 2(по восемь)=8 клеток. Или троеточие как то считать нужно?
конечно нужно )
два по 4, два по 5, два по 6, два по семь
Если у нас есть длинный ряд чисел, то для упрощения записи все элементы не пишутся, а только несколько первых и последний, а середина заменяется многоточием. Так же пишется бесконечный ряд, последний элемент в этом случае значок бесконечности.
...а от куда взялись столбики из 5 и 7 кубиков???
Из многоточия.
Хорошая задачка. При её решении школьник сам осознает о существовании такого явления как вероятность.
Если конечно сам решает.
Ответ: 21 (очко). Путем исключений на Д2 и Д4 или 6 или 7, в каком порядке для решения задачи не важно.
неее тема кубиков не раскрыта!!!
7 и две 8 итого 23
две 8-ки не могут быть. обе восьмерки во второй сверху строчке
Тоже так пронял8+8+7=23
21. думал 4 минуты. сейчас просмотрю, правильно ли ))
p.s. или у дураков мысли сходятся, или мы молодцы ))
Какая то муть, можете набить морду автору задачи
предложение поддерживаю, хотя задача интересная, да и результат - 21 очко, впечатляет)
Да сплошная логика, методом исключения. Но блин 6 класс, че рехнулись что ли. Это ж какой должен быть мозг и какое тело.. Хиляков взращивать...Так они потом до пенсии не дотянут...
Ну почему сразу хиляков? Пусть детвора развивает образное мышление. Хотим стать лидерами - надо учить детей решать нетривиальные задачи.
Вот китайцы, например, своим задают такие задачи: Медведь упал в яму-ловушку глубиной 19,617 метров. Время его падения составило 2 секунды. Какого цвета был медведь? и ничего, решают ведь)
А уж как Нильс Бор решал задачи на вступительных - вообще классика!
А зачем нам китайцы??? Вы нам еще монахов из Шаолиня подкиньте, а шо пускай развивают кунгфу.
Вы нам еще монахов из Шаолиня подкиньте, а шо пускай развивают кунгфу.
Ото сбили людей этим космополитизмом.
Нильс Бор когда решал задачи на вступительных никто на него и не смотрел, это уже потом когда он стал Бором, настало время офигетельных историй.
Вот тут можете почиталь как Относились к Шаубергу пока он не стал Шаубергом. Ну стандартно же. Логично, разве нет???
https://aftershock.news/?q=node/263350&full
большое спасибо за статью, очень познавательно. Надо будет поподробнее почитать про Виктора Шаубергера.
Но речь немного о другом. Он - талантливый самоучка, а мы говорим о системной подготовке думающей молодежи. И данные задачи - шаг в верном направлении.
Не факт не факт. Тут надо знать что являеться верным направлением в Вашем понимании.
Не за что, всегда пожалуйста
Задача скорее на логику и пространственное мышление, но, конечно, если никогда подобного рода задач не решал, то может привести в замешательство.
в середине 8 снизу 6 и 7 всего 21
Вид спереди два выделенных столбца по 8.
ПыСы.понял до конца условия не дочитал.
Я конечно еще тот математик))
Но что если предположить, что вся поверхность доски занята кубиками. То что нарисовал Никита это только его распределение кубиков на поверхности. Тогда получается, что кубиков нужно 36 штук.
Блин, до конца условие не дочитал)) Действительно ответ 21 кубик.
Вообще-то, однозначно можно расположить только восьмерки, остальные только или-или, поэтому и спрашивают сумму кубиков, а не конкретное количество в каждой клетке.
8-7-6 или 8-6-7 =21
Я то же считаю, что тема кубиков не раскрыта. Если посмотреть на вид спереди и справа, получается что в крайней клетке (общей как для вида спереди, так и для вида справа) должно быть одинаковое количество кубиков, а в условии задачи, при виде спереди восемь кубиков, а при виде справа - семь, как такое может быть???!
Может, может.
Вот представьте стакан, для простоты цилиндрический. Тень от него на параллельной стакану стене при освещении и спереди, и сбоку будет в виде прямоугольника, несмотря на то, что это цилиндр.
Да))) я уже поняла свою ошибку!)
Страницы