Представьте себе совершенно дикий по идиотизму пример.
- Допустим, что в наше время общепринятым представлением о мироустройстве является геоцентрическая система: центральное положение во Вселенной занимает неподвижная Земля, вокруг которой вращаются Солнце, Луна, планеты и звёзды. И этим представлениям о мироустройстве уже 300 лет.
- Но 10 лет назад была сформулирована альтернативная — гелиоцентрическая гипотеза: будто Земля и другие планеты вращаются вокруг Солнца.
- А в 2016 году двумя известными физиками (один из них Нобелевский лауреат, совершивший переворот в физическом представлении о мире) была опубликована статья, в которой гелиоцентрическая гипотеза доведена до уровня физической теории (эта статья стала самой читаемой научной публикацией года в журнале).
- И совсем недавно — в июле сего года вышло экспериментальное психологическое исследование, показывающее, что вшитые в человека от рождения нейробиохимические механизмы (биоритмы и т.д.), как бы настроены на то, что Земля вращается.
И не смотря на все это, геоцентрическое представление о неподвижной Земле остается общепринятым. А присущее людям врожденное представление о вращающейся Земле признано иррациональным искажением несовершенной человеческой психики…
Согласитесь, — пример действительно дурацкий.
Разве подобное возможно?
Оказывается, да. Вот уже 300 лет люди используют концептуально несовершенную и потому ошибочную концепцию вероятности. Все к этому за 300 лет привыкли…
И вот в начале декабря случилась сенсация.
Авторитетный научный журнал Nature Physics публикует статью «The ergodicity problem in economics». Ее автор Оле Питерс — продолжает тему, начатую в знаменитой статье 2016 года «Evaluating gambles using dynamics», написанной совместно с нобелевским лауреатом великим Мюрреем Гелл-Манном (тот, к сожалению, уже умер).
В новой статье утверждается, типа, —
«И все-таки она вертится!».
В смысле, что пора науке решиться и поменять-таки представления о вероятности. Потому что, если коротко, ситуация такова.
- Многие современные науки основаны на искаженном представлении о реальности. Это искажение является следствием сложившихся около 300 лет назад ошибочных представлений о вероятности (риска, удачи, счастья …).
- Лежащее в основе этих представлений формальное понимание математики случайности 300 лет назад было в зачаточном состоянии и концептуально наивно. Предполагалось:
- что случайность, возникающая в единственно существующем пространстве с необратимым временем, имеет тот же эффект,
- что и случайность, возникающая в ансамбле параллельных вероятностных миров. - В 18 веке экономика (первая дисциплина, веком раньше разработавшая математику случайности ) заметила нестыковки теории и практики, возникающие из-за подмены временной вероятности на ансамблевую, и разработала инструменты (типа теории полезности), хоть как-то смягчающие некоторые из нестыковок. Там же, где наблюдалось резкое отклонение поведения людей от предсказаний экономических моделей, просто было объявлено, что это следствие иррациональности человеческой психики.
- В 19 веке в физике, а именно в термодинамике и статистической механике, была разработана новая концептуализация случайности. Эта концептуализация с самого начала признавала центральную роль времени в случайных процессах. Тем самым в физике был устранен фундаментальный недостаток — путаница в применении временной и ансамблевой вероятностей.
- В экономике же и прочих неточных дисциплинах, изучающих принятие людьми решений в условиях неопределенности (финансы, социология, психология и т.д.), все пока что остается, как и 300 лет назад.
В результате этого человечество имеет массу проблем:
- неизбывное наступание на грабли ошибочных решений (и в том, числе, крайне важных), основанных на неверных методах управления рисками, базирующихся на изучении прошлого;
- наличие неразрешимых парадоксов, головоломок и аномалий, беззащитность перед «черными лебедями» и т.д.;
- доминирование в мире модели рациональности, не соответствующей человеческому опыту и тому факту, что люди живут в единственно существующем пространстве с необратимым временем, а не в параллельных вероятностных мирах.
Чтобы исправить все это, необходима смена человечеством модели рациональности. А это влечет за собой будет весьма серьезные последствия:
— полный пересмотр экономической теории и практики финансовых спекуляций;
— кардинальное изменение трактовки причин нарастающего неравенства;
— принципиальная смена подходов в практике прогнозирования и принятия решений;
— отказ от использования многих привычных показателей и индикаторов (типа понятия ВВП в качестве индикатора уровня процветания);
— демонтаж и замена существующих систем страхования и пенсионной системы
… и много чего еще.
✔️ Так что ж, если такая научная трактовка прошла рецензирование и опубликована в Nature Physics, — мы на пороге новой научной революции?
Полагаю, что это весьма возможно. Но решать не мне.
Моя же задача — всего лишь попытаться на простом языке объяснить, в чем суть крупнейшего прорыва человечества в понимании случайности.
И желательно, чтобы каждый из читателей мог проверить это на простом и интуитивно понятном примере. С которого мы и начнем.
Из прошлого в будущее много путей, но реализуется лишь один
«Учитывая ход времени, ваша способность играть в игру завтра зависит от последствий сегодняшних решений».
Оле Питерс
Bот уже 300 лет считается, что поток времени не имеет отношения к вероятности. Но это не так. На самом деле, существуют два типа вероятности: временная и ансамблевая. Проще всего понять разницу между ними на простом примере игры в орлянку. Эта простая игра хорошо иллюстрирует общепринятый способ мышления при оценке вероятности и принятия решений в рисковых ситуациях, зависящих от случайности.
Игра такова.
- У меня $100 (это мой начальный баланс).
- Я подбрасываю монету (она симметричная и бросаю ее без жульничества).
- Если выпадает орел, я выигрываю 50% от моего текущего баланса.
- Если выпадает решка, я теряю 40% текущего баланса.
Таким образом, если после 1го броска монеты выпадет орел, я выигрываю $50, а если решка, то потеряю $40.

С такими правилами игра выглядит весьма привлекательно, хотя и есть, конечно, некоторый риск.
Под риском понимается ситуация, когда, зная вероятность каждого возможного исхода, все же нельзя точно предсказать конечный результат. Но можно оценить риск и потенциальную выгодность игры. Дабы принять решение — играть в нее или нет.
Напомню.
Ожидаемое значение случайной величины (в нашем примере, очередной орел или решка) подсчитывается по формуле математического ожидания:
Е(х) = p1*х1 + p2*х2 + … + pn*xn
где р1, р2, … pn — вероятности каждого исхода, х1, х2, … xn — значения каждого исхода: либо прибавка 50% к текущему балансу, либо его сокращение на 40%.
Тогда, математическое ожидание денежного выигрыша после первого броска монеты, составляет (0,5*$ 50 + 0,5*$ — 40) = $5 или 5% прироста текущего баланса. Рассуждая дальше, матожидание денежного выигрыша после второго броска монеты составляет (0,5*52,5 + 0,5*$ -42) = $5,25. Еще 5% прироста текущего баланса.
Предполагается, что этот процесс с течением времени будет генерировать 5%-ную скорость роста денежного выигрыша. И если играть достаточно долго, эта скорость будет все более приближаться к своему расчетному значению 5%.
Теперь начинаю играть.
Желающие могут далее
- либо смотреть видео, на котором Оле Питерс рассказывает (по англ.) о ходе игры и обнаруживаемых поразительных сюрпризах;
- либо читать далее эту главу, где поясняющих картинок будет даже больше, чем в рассказе Оле.
Игра в миллионе параллельных реальностей
Бросаю 5 мин (по 1 броску в минуту). Получилось вот что. Красная линия показывает состояние текущего баланса после броска. Первые 2 раза была решка, потом орел, снова решка и опять орел.
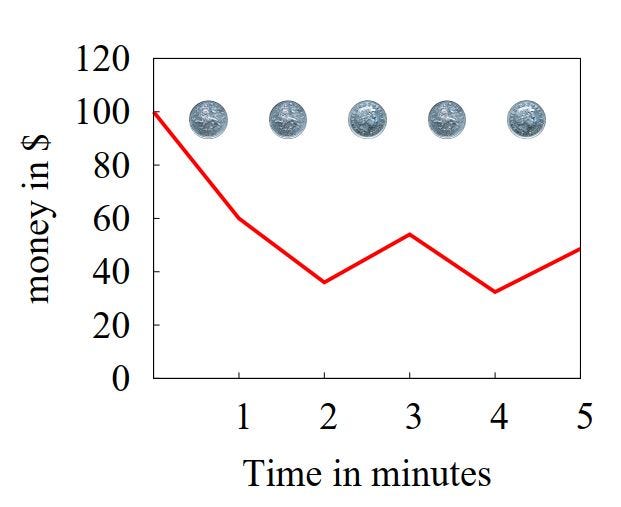
Пока что ожидаемого 5%ного роста дохода не видно. Проклятая случайность играет против меня. Это ничего. Нужно просто подольше поиграть, чтобы флуктуации случайности уравновесились. И никуда оно не денется, в среднем все придет к обещанным 5%.
Играю дальше еще 55 мин (все так же, по броску в минуту). Получилась 60-минутная серия бросков.
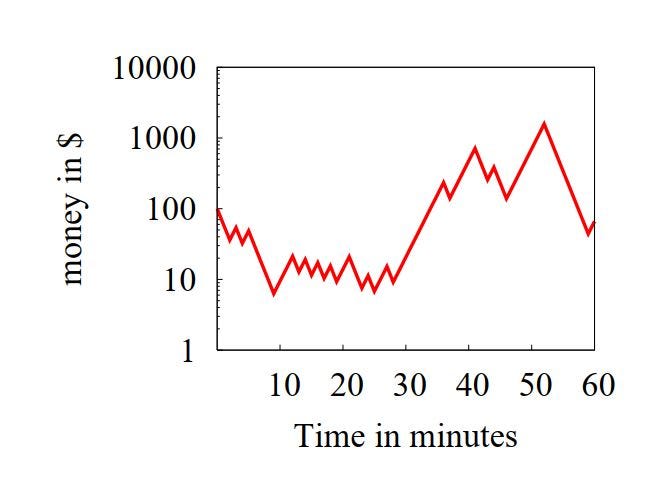
Был и в проигрыше, и в выигрыше. Но все равно, что-то тренда пока не видно. Все забивают флуктуации случайности. Не хай. Буду дальше играть, и все само образуется. Сделаю еще 9 таких же серий, чтоб всего было 10 серий по 60 бросков.
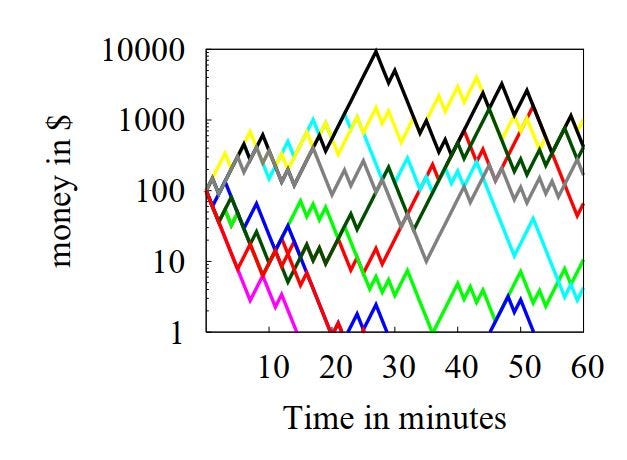
Кто-нибудь видит здесь хоть какой-то тренд? Я не вижу. Значит все еще мало бросали. Делаю еще 10 серий. Итого получаю 20 серий бросков по 60 раз.
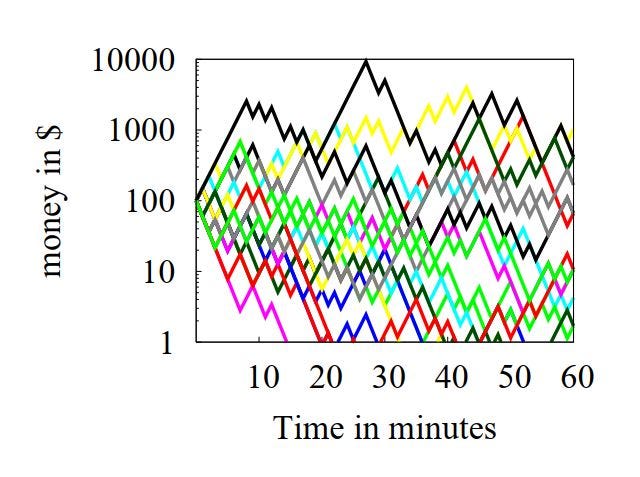
От результатов начинает рябить в глазах. Но тренд на 5%ный выигрыш, хоть убей, не просматривается. Понимаю, что зря я на эту рябь смотрю и нужно просто посчитать средние поминутные значения по всем 20 сериям. Получается вот так.
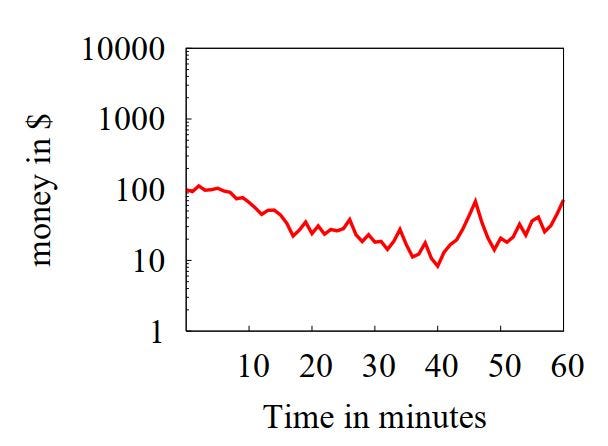
Тренда пока не просматривается. Но я не сдаюсь. Делаю 1 тыс. серий и вычисляю для каждой минуты средние значения…
Тру-ту-ту-ту! Приз в студию! Вот что получилось.
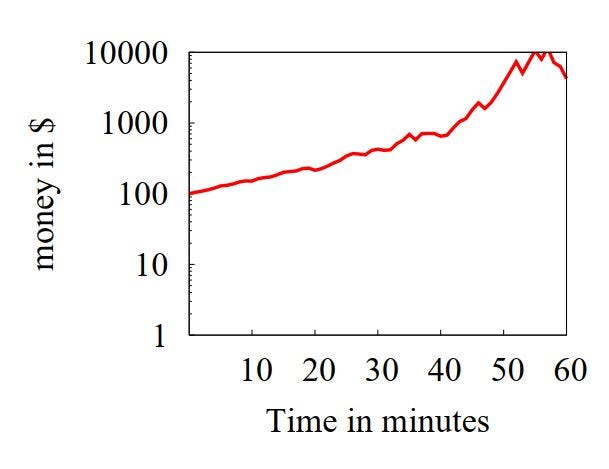
Чем ни тренд? Жаль только в конце график почему-то вниз повалился. Надо еще больше серий сделать.
Делаю 1 миллион серий. И каков результат — загляденье!
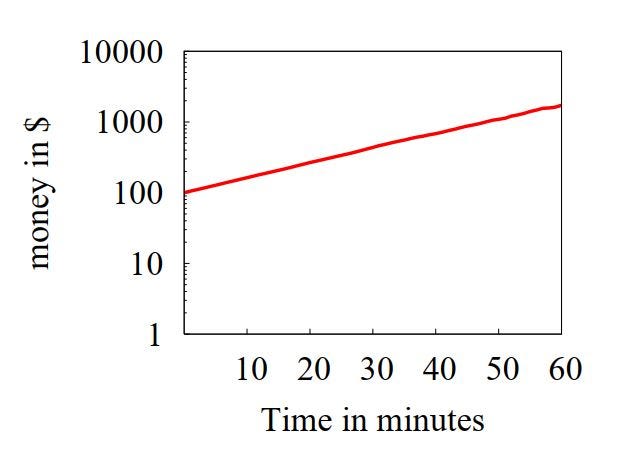
Четкий линейный тренд с ростом дохода в 5%. Игра, как и подсказывала интуиция, выгодная. Нужно было лишь подождать, чтобы в результате многих бросков отфильтровался шум случайностей. Что и было получено.
Но постойте. Надеюсь вы понимаете, что на самом деле,
я не бросал монету 114 лет, чтобы сделать 1 млн. серий по 60 бросков в час.
Вместо этого я рассчитал средние значения по 1 млн. ансамблей, каждый из которых состоял из 60 бросков за час.
Каждый ансамбль имел свою траекторию, которая для простоты различия была покрашена в уникальный цвет, как было показано на картинке из 20 траекторий.
✔️Но что означает тот факт, что полученное мною итоговое усреднение было сделано для 1 млн. траекторий?
- Я как бы набрал 999999 студентов и одновременно с ними сделал 1 млн. серий, каждая из которых включала 60 попыток по одной в минуту?
Как будто каждый из нас делал свою серию в собственной параллельной реальности, а результат я просто усреднил по всем этим реальностям.
Но нет у меня никаких параллельных реальностей.
Кроме того, в некоторых параллельных реальностях (на части траекторий) я проигрался в ноль, не завершив серию. А ведь в жизни-то я так не смогу: если на одной траектории проигрался, просто возвращаюсь во времени назад и перехожу на более удачную траекторию.
Нет, это какой-то бред. Надо уходить от параллельных реальностей.
Но что получится, если я буду делать свои попытки один, — в необратимом потоке времени, так сказать, в единственной доступной нам реальности?
Игра в единственной существующей реальности
Начну, как и раньше, сделав 60 бросков.

Потом просто стану бросать дальше в течение суток.
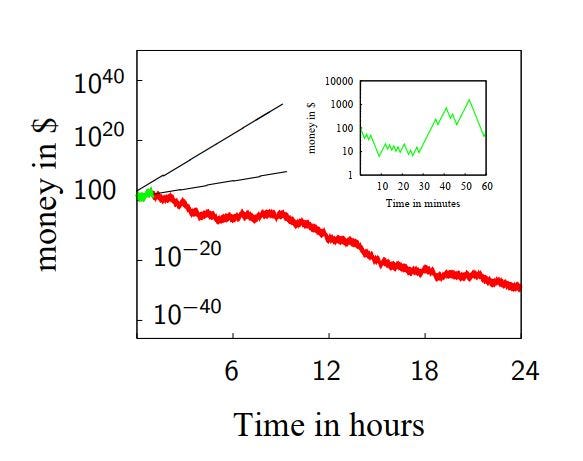
По горизонтальной оси теперь откладываются не минуты, а часы. Зеленым цветом в левой части красного графика показана траектория 1го часа игры, вынесенная на вставку в правой верхней части рисунка.
Продолжаю играть все ту же единственную игру. Но черт побери! Я все больше и больше проигрываю. Начальные 100 баксов быстро растаяли до малых долей цента. Попробую играть целую неделю. Вдруг начнет везти.
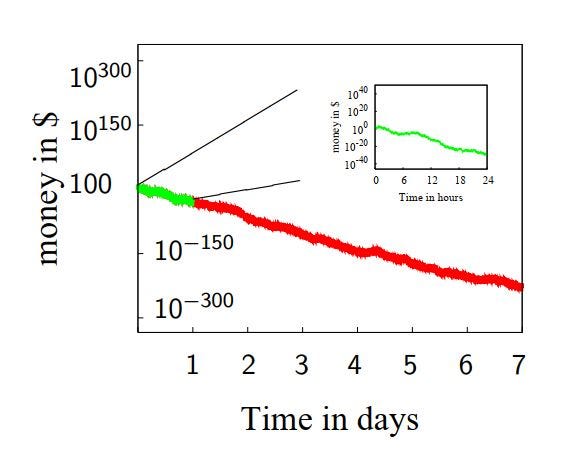
Теперь по горизонтальной оси показаны дни. А результат становится все хуже и хуже. Флуктуаций, правда, становится все меньше. Но тренд однозначно направлен на безальтернативный проигрыш. Но я упорный. Буду играть целый год.
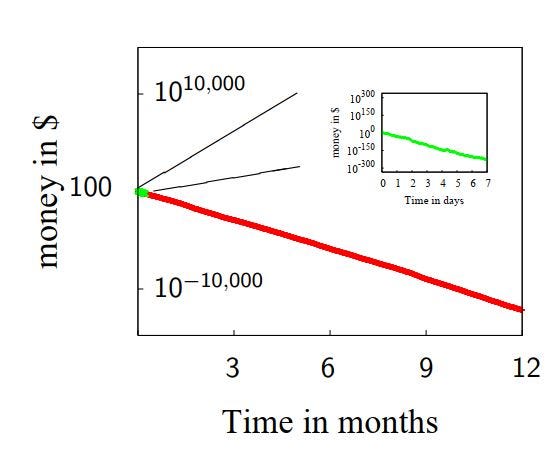
Теперь по горизонтальной оси уже месяцы. Флуктуации окончательно сгладились. Но результат ужасен.
✔️В чем же дело? Почему получились две несравнимо разные картины?
- В ансамблевом варианте, когда были усреднены 1 млн. игр, как бы сыгранных в параллельных мирах 1 млн. людей, получился ожидаемый выигрыш.
- В единственной игре, сыгранной мною за целый год, я проигрался в пух и прах.
Получается, как будто:
— если играет большое количество людей (ансамблевой вариант), средний результат получается положительным (что не удивительно, т.к. ожидаемый выигрыш игры положительный);
— но если кто-то один достаточно долго играет в эту игру (временной вариант), он теряет почти все свои деньги.
Какой-то бред сумасшедшего получился!
Может ошибка какая вкралась?
Надо проверить оба варианта на симуляторе.
Проверка ансамблевого варианта
Желающие могут сами это сделать, воспользовавшись анимированным симулятором игры, запрограммированным Сидом Шанкером (правила в этой игре чуть-чуть численно отличаются: за орла и решку выдается не +50% и -40%, а +55% и -45%, но это принципиально ничего не меняет).
В ансамблевом варианте в игру играют 40 человек, и каждый бросает монету 20 раз. Начальный баланс у всех одинаковый — $100.
Вот перед вами итоги 4х игр (вы сами можете сгенерировать еще хоть 1000 подобных игр на симуляторе).
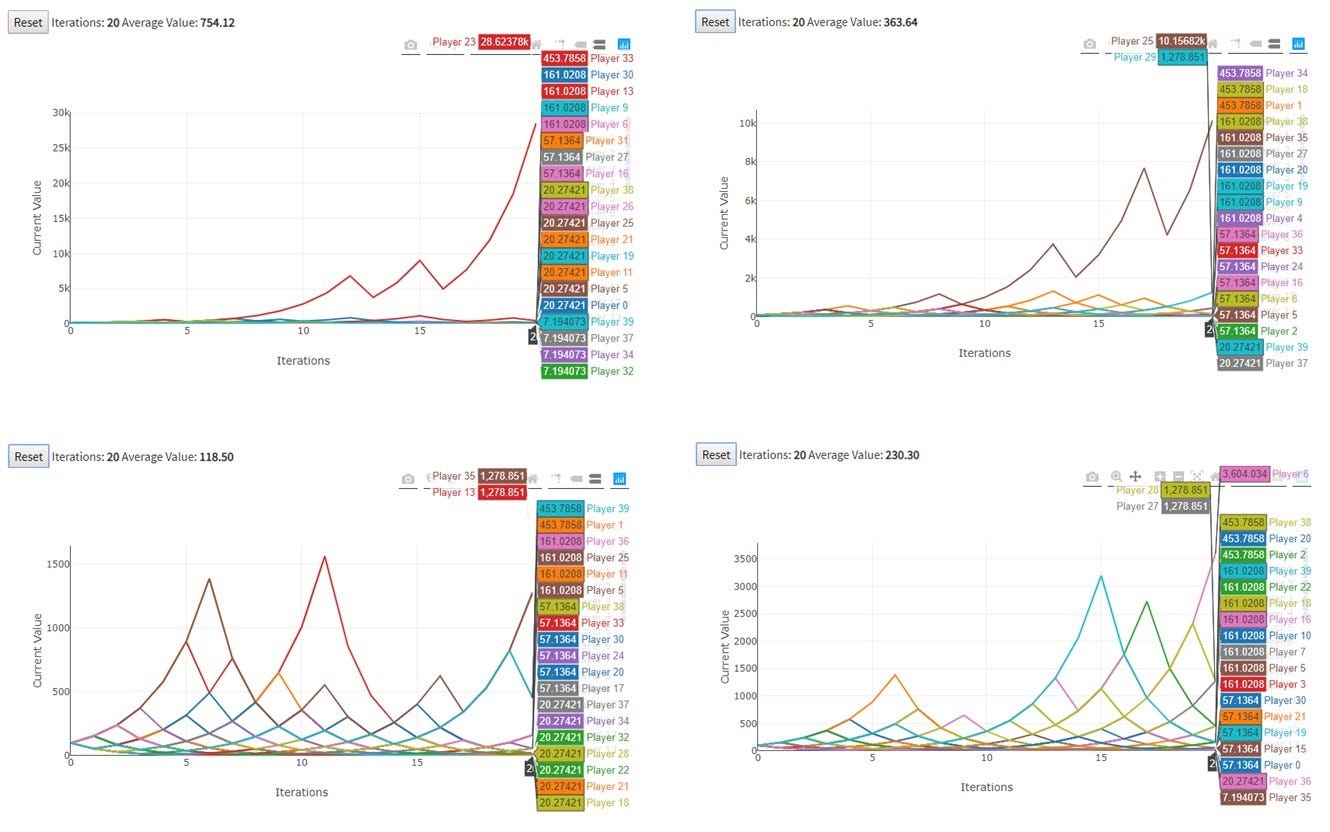
На вышеприведенной картинке показано для каждой из 4х игр:
- траектории выигрыша двадцатки (больше на анимированном графике не умещается) наиболее успешных (по размеру итогового выигрыша) игроков;
- сумма итогового выигрыша этой же «великолепной двадцатки» после последнего 20го броска (на анимированном графике симулятора, перемещая курсор, можно смотреть также все промежуточные результаты после каждого броска);
- среднее значение итоговых выигрышей всех 40 игроков.
Что особенно интересно.
— Среднее значение выигрыша для всех игроков в конце игры (указано сверху слева), как правило, выше $100 (оно и понятно, игра же выгодная).
— Однако, как правило, в результатах получается огромный разброс. Почти всегда, один или два игрока выигрывают большие деньги, тогда как большинство теряют.
Например, в 1й (самой «несправедливой») игре, средний итог игры составил аж $754, но это большущее среднее получилось так:
- игрок №23 огреб $28+ тыс.,
- а игроки №№39, 37, 34, 32 (а также игроки 2й («омерзительной») двадцатки, продули почти все, имея к концу игры лишь по $7.
А в самой «справедливой» 3й игре, средний итог игры составил $118, а это скромное среднее получилось из такого разброса:
- игроки №№35 и 13 огребли по $1279,
- а игроки №№37, 34, 32, а также №№28, 22, 21, 18 остались после игры всего с парой десятков баксов (а игроки «омерзительной» двадцатки еще с меньшими суммами).
Возникает резонный вопрос.
✔️С кем из игроков я должен себя ассоциировать при принятии мною решения?
И вообще:
— выгодная это игра или нет?
— стоит ли мне в нее играть?
Мне равняться на результат игрока №23, что огреб $28+ тыс. в 1й игре?
Или на его же результаты в играх с 2й по 4ю, где он сильно продул, не выйдя из «омерзительной» двадцатки?
Ведь ориентироваться на среднее между всеми игроками нет смысла: я же один буду играть и всего один раз, сделав 20 бросков монеты.
Попробую снова воспользоваться анимированным симулятором игры Сида Шанкера, чтобы проверить, что меня ждет если я буду долго играть один (временной вариант).
Проверка временного варианта
В этом варианте симулятора вы просто жмете на «Play» (на статичном рисунке ниже это клавиша в состоянии «Сброс»/«Reset», т.к. это скриншоты с анимации) и игра идет до бесконечности, совершая все новые и новые случайные броски монеты и, соответственно, увеличивая или уменьшая текущий баланс игрока.
Вот пример одной игры.
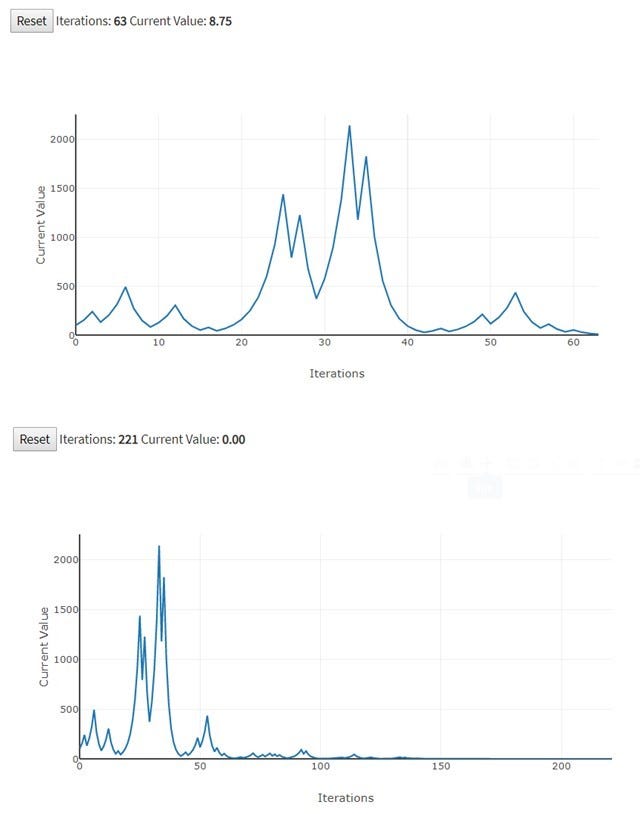
На верхнем графике показана траектория текущего баланса игрока до 65го броска монеты. Как видите, 35 бросков сказочно везло, что позволило на 33м броске довести выигрыш до $2 тыс. Но потом везение кончилось, и к 65у броску баланс устремился к нулю.
Подобный плачевный итог повторился в еще паре десятков игр, сыграных мною на симуляторе.
Вот 4 из них в качестве примера. Игры довольно длинные (количество бросков монеты: 158, 175, 652 и 872), чтобы не вкралось сомнение, будто их плачевный исход — плод недостаточно длинных серий бросков.
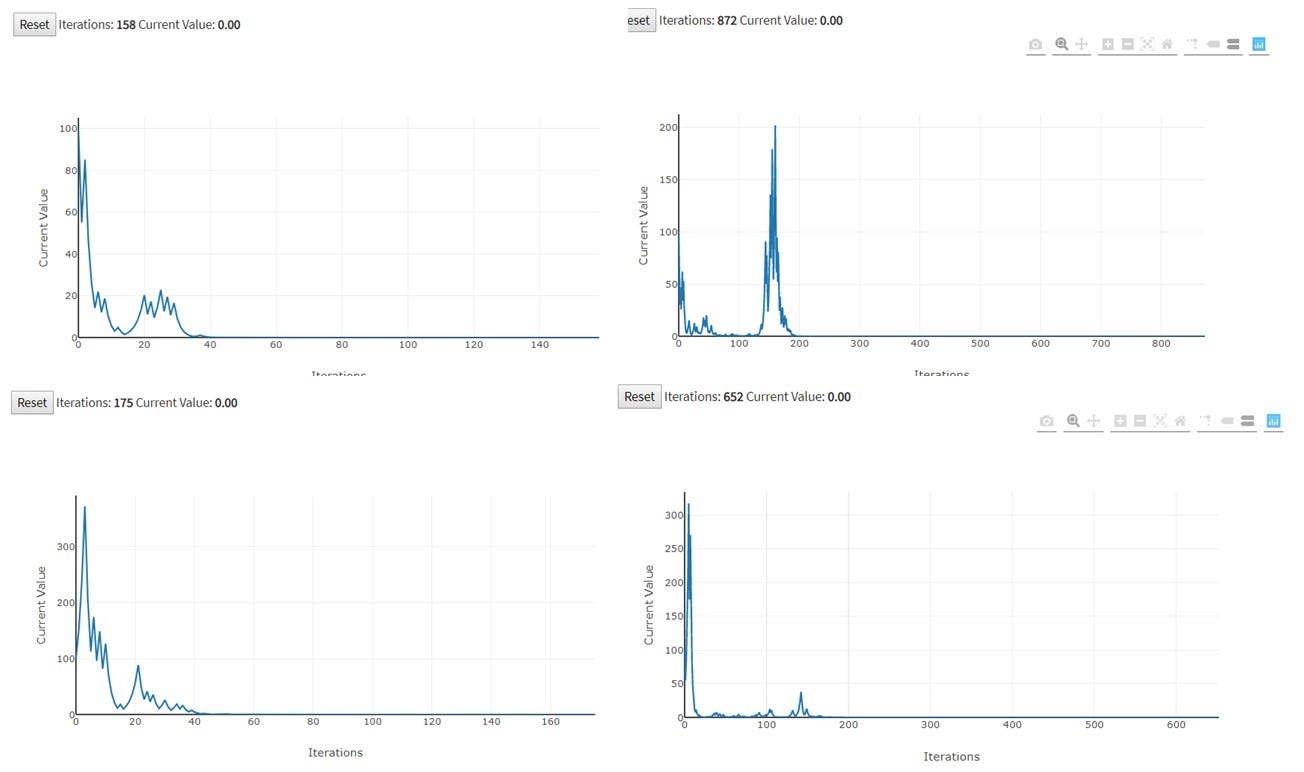
Увы. Исход у меня получился всегда один и тот же.
- Были взлеты и были падения.
- Но, в конечном итоге, мой баланс всегда стремился к 0.
Т.е. игра, в которой каждый ход имеет положительное ожидаемое значение выигрыша, в конечном итоге ведет к абсолютному проигрышу.
Вывод
Проверка на симуляторе подтвердила наш предварительный довольно нелогичный вывод.
В 2х вариантах этой игры получаются кардинально разные результаты.
✔️Когда много людей играют в игру небольшое количество раз, происходит усреднение по ансамблю, и ожидаемый выигрыш положительный.
✔️А когда один человек играет в игру много раз, происходит усреднение по времени, и ожидаемый выигрыш отрицательный (то есть неотвратимый проигрыш).
- В ансамблевом варианте 1 млн. человек играли по часу в неких параллельных реальностях. В среднем у них получился устойчивый выигрыш. При этом, правда, большинство игроков из параллельных реальностей проиграли. Но зато один или двое из них сорвали большой куш. И этот куш столь велик, что, если сложить его с теми крохами, что остались у большинства, среднее значение выигрыша получится положительным.
- Во временном варианте 1 человек играл целый год и проигрался в дым, поскольку у него была всего одна игра и откатить назад во времени (если вдруг проиграл) он не мог.
✔️ Но как же такое может получаться — игра одна, а результаты разные?
Оказывается, ничего удивительного. Просто в данном примере мы столкнулись со случайной системой, являющейся неэргодичной.
Эргодичность
«Нет вероятности без эргодичности»
Нассим Талеб
Мы привыкли, что вероятность, применимая к группе людей (ансамблевая вероятность) и вероятность, применимая к одному человеку (временная) совпадают.
Если вы бросите игральную кость 100 раз, сколько раз выпадет шестерка? Нет сомнений, что где-то в районе 17 раз.
А если попросить 100 человек по разу бросить кость, то сколько шестерок в сумме у них выпадет? И опять нет сомнений, — тоже примерно 17.
Т.е. получается, что в примере с игральной костью среднее по времени и среднее по ансамблю получаются одинаковые, а в примере из предыдущего раздела поста — с бросанием монеты и +50%ным или -40%ным изменением баланса — они разные.
Объяснение этому отличию было предложено еще в 1884 великим австрийским физиком-теоретиком, основателем статистической механики и молекулярно-кинетической теории Людвигом Больцманом.
Он ввел новое понятие — эргодичность для процессов, в которых среднее по ансамблю и среднее по времени совпадают.
Такие процессы были названы эргодическими. Соответственно, процессы, в которых эти 2 средних не совпадают, были названы неэргодическими.
Это слово, являющееся определением важнейшего класса случайных процессов, столь редко в использовании, что Google на запрос «неэргодический» дает всего около 600 ссылок (для сравнения, на запрос «вероятность» выдается 63+ млн. ссылок — в 100 тыс. раз больше). И это соотношение таково, поскольку, на самом деле, лишь 1 человек из примерно 100 тыс. слышал, что бывают неэргодические случайные процессы. А их в реальной жизни пруд пруди, т.к.
сама жизнь по своей природе неэргодична,
— время в жизни необратимо, и каждый из нас живет в единственном варианте реальности, не предлагающем нам иных средних значений, чем среднее по времени.
Если мы, оценивая рискованность (привлекательность) какого-то своего действия (напр. инвестиции или ставки в игре случая), не заморачиваемся с вопросом эргодичности, это грозит нам печальным результатом. Как было показано в предыдущем разделе,
можно полагать ожидаемую доходность игры (или любого иного процесса, где правит бал случай) положительной, тогда как, на самом деле, она отрицательная.
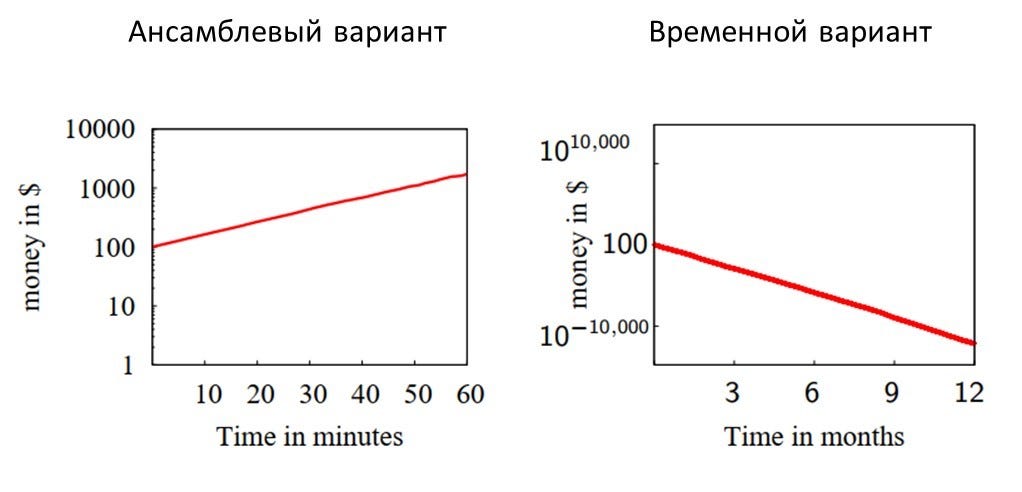
Напомню уже известный вам рисунок.

Такое запросто может быть в жизни. Вы полагаете, что у вас будет гарантированный плюс (левый график), а вас ждет непременный минус (правый график).
✔️ Но в чем же коренится столь коварная иллюзия?
✔️ Что заставляет человека столь кардинально лопухнуться с оценкой перспектив, приняв неэргодический процесс за эргодический?
Причин, по большому счету, две.
Первая, — замена временной вероятности на ансамблевую.
В этой простодушной замене при оценке ожидаемой выгоды, среднее по времени просто заменяется на среднее по ансамблю. Это ловкий трюк, многим кажется чрезвычайно полезным, так как ансамбль средних значений, как правило, значительно проще и, главное, гораздо быстрее вычислять по сравнению со средним по времени. Ждать, когда последовательно произойдет множество событий, долго. А как говорил О.Бендер, — время, которое у нас есть, — это деньги, которых у нас нет.
Вот только выходит потом себе дороже. В итоге такой замены для неэргодических процессов (коих в жизни предостаточно) мы обрекаем себя на ошибочную оценку перспектив.
Другая причина — наличие в жизни необратимых последствий.
В результате этого,
для неэргодических процессов наблюдаемая в прошлом вероятность не применима к будущим процессам.
Нассим Талеб называет такие необратимые последствия «гибелью» — попаданием в экстремально поганую ситуацию, не подразумевающую восстановление.
Поясняя это, Нассим Талеб использует такой экстремальный пример, использованный им в качестве базового объяснения в книге «Одураченные случайностью».
Предположим, что шестеро людей играет в русскую рулетку: каждому по выстрелу и приз в $1 млн. долларов.

После шести выстрелов, скорее всего, пять из шести играющих останутся в выигрыше. Если использовать стандартный анализ выгоды и затрат, можно утверждать, что вероятность выигрыша у каждого из игроков составляет 83,33%, а «ожидаемый» средний доход в результате каждого выстрела составит около $833333. Но проблема в том, что при многократной игре в русскую рулетку (более одного прохода по всем стреляющим) кто-то непременно попадет на кладбище. И поэтому, ожидаемый доход… просто не вычисляем.
Этот пример запросто переносится на куда менее экстремальную игру в казино.
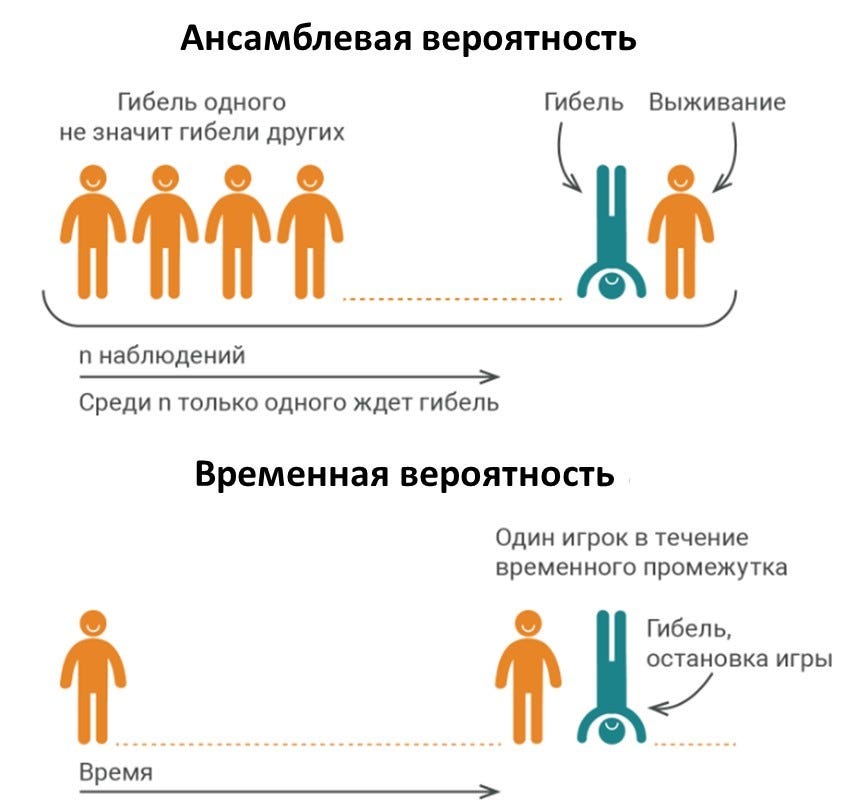
На рисунке показана разница между ситуациями, когда:
- 100 человек идут вечерком развлечься в казино, и кому-то, возможно, не повезет (верхний рисунок);
- один человек ходит в казино каждый день в течение 100 дней.
В первом варианте нет никакой зависимости от каких-либо событий в прошлом. И потому привычное понимание вероятности (ансамблевой) здесь вполне применимо. А если кто-то из 100 пришедших проигрывает все, что имел, — это, при расчете средних значений, как бы происходит в одном из «виртуальных вероятностных миров», а во всех остальных «мирах» (где как бы играют другие 99 игроков) все нормально.
Второй вариант совсем иной. В нем вероятность зависит от прошлого. Идя в казино сотый раз человек имеет за плечами 99 предыдущих игровых вечеров. Поэтому:
- здесь не только должна применяться другая вероятность — временная, вместо ансамблевой,
- но и «гибель» — полный проигрыш человеком всего, что у него есть, — происходит отнюдь не в одном из «виртуальных миров», а в единственно существующем для него мире.
И естественно, что после «гибели» уже нет смысла рассчитывать ожидаемый доход от новых походов в казино, даже если «гибель» случилась в первый же вечер. Этой вероятности просто не существует, поскольку больше походов в казино уже не будет.
Ошибка неразличения 1го и 2го вариантов сохраняется в экономике, психологии и социальных науках с незапамятных времен.
А в наши дни это неразличение разных вероятностей при анализе больших данных (основанном на вероятности больших ансамблей) грозит еще большим масштабом заблуждений и ошибочных решений при:
- оценке ситуаций,
- выборе вариантов действий,
- анализе поведения и пристрастий людей,
- прогнозировании сценариев развития событий.
Т.е. по сути, это равносильно жизни людей в некой искаженной реальности, где оценка ими вероятности многих событий просто ошибочна.
Но люди привыкли. Ведь человечество живет в этой искаженной реальности уже около 300 лет, с тех пор, как пути ансамблевой и временной перспектив разошлись.

Как видно из рисунка, за обе перспективы (ансамблевую и временную) топили многие великие умы.
Но в итоге, к концу 2019 мир живет все в той же искаженной реальности, изобилующей старыми парадоксами и новыми ошибками.
Рассмотрим чуть подробней конкретные последствия подобных ошибок.
Цена искаженной реальности
«Экономика так и не состоялась, как наука, поскольку мы должным образом так и не определились с ее основанием. Если в экономике никогда не было Галилея, как же здесь могут появиться Ньютон или Эйнштейн?»
Джеффри Уэст
Вынесенные в эпиграф слова Джеффри Уэста, на мой взгляд, исчерпывающе описывают состояние современной экономики, как науки.
- Экономика — это наука.
- Но ее уровень сейчас примерно таков, как в физике был до Галилея.
- Причина же этого в зыбкости и неопределенности основ этой науки — оценки выгоды и рисков экономической деятельности.
Сегодняшнее управление рисками часто полагается исключительно на инвесторов, определяющих свои предпочтения в отношении риска через функцию полезности без явного учета влияния времени.
Литература по управлению капиталом и управлению рисками в значительной степени использует комбинация средних значений ансамбля и полезность, пренебрегая временем или в лучшем случае инкапсулируя его эффекты в функции полезности. При таком подходе необратимость времени, непоколебимая физическая мотивация воздержания от чрезмерного риска, заменяется произвольно определяемым риском предпочтения. После создания соответствующих академических рамок (примерно с 1970-х годов), нормативные ограничения, которые были в значительной степени основаны на здравом смысле, были постепенно ослаблены.
В итоге, ранние математические методы, разработанные в экономике в 17 и 18 веках, по-прежнему лежат в основе многих проблем, стоящих перед современной теорией экономики. Их нужно менять, исправляя наивные взгляды на случайность.
Новая теория экономики должна учитывать понятие эргодичности, разработанное в 20-м веке и без которого немыслима современная физика.
Так почему же это не делается?
Прямолинейный Нассим Талеб винит тупость и упертость экономистов. Более политкорректные специалисты объясняют это мотивацией ключевых акторов, заинтересованных, чтобы ситуация не менялась.
- Страховщики заинтересованы продолжать свой немалый бизнес. А при переходе к «эргодической экономике» его можно будет закрывать. Как минимум в том виде, в каком он существует сегодня.
- Правительства заинтересованы продолжать балаган с пенсионными системами. А при переходе к «эргодической экономике» они просто накроются медным тазом, в связи с осознанием их ненужности.
- Международные эксперты, как и правительства всех стран, заинтересованы продолжать морочить людям голову, измеряя рост благосостояния в стране показателями ВВП и ВВП на душу населения. А при переходе к «эргодической экономике» всем станет понятно, что этот показатель имеет весьма косвенное отношение к росту благосостояния страны, ибо его довольно просто увеличить, сначала выкопав котлован на полстраны, а затем его закопав.
- Богатая «элита» заинтересована продолжать объяснять растущее имущественное неравенство всем, чем угодно, но не тем, что иначе быть просто не может при современном устройстве экономики, где правит «закон Матфея». А при переходе к «эргодической экономике» все псевдо-объяснительные уловки вылезут наружу, и потребуются совсем иные методы и механизмы выравнивания экономического неравенства.
Похожая картина с мотивацией ключевых акторов, заинтересованных, чтобы ситуация не менялась, царит в социологии, психологии и прочих науках, создающих теории поведения и деятельности людей в условиях реальной жизни.
Ведь как я уже писал выше.
Жизнь, сама по себе, неэргодична.
Она неповторима и нетиражируема в других вероятностных реальностях, протекая в необратимом потоке времени.
И, что самое интересное, — свойство чувствовать разницу между эргодическими процессами и неэргодическими в вероятностном пространстве жизни, встроено в нас, подобно чувству ориентации в окружающем нас 3х мерном пространстве.
В этом году было доказано —
люди интуитивно различают эргодические процессы от неэргодических.
Экспериментальная проверка показала, что, вопреки современной науке, люди отказываются от стратегии линейной оценки полезности, когда сталкиваются с процессами с мультипликативной динамикой (как в примере с монетой, где выигрыш оценивался мультипликативно — в процентах от текущего баланса). При смене динамики процесса с аддитивной (выпал орел — получи $50, выпала решка — отдай $40) на мультипликативную, люди, как показал эксперимент, интуитивно переходят на логарифмическую оценку полезности на (см. рис. ниже).
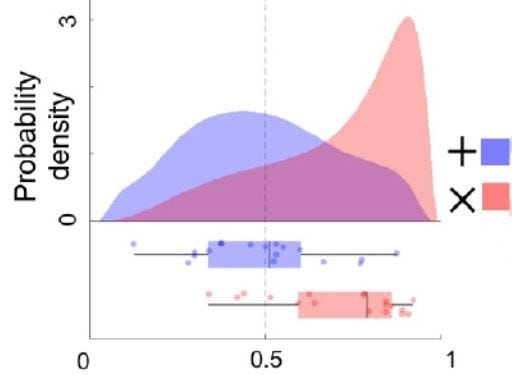
На этом рисунке показано, что, в зависимости от динамики азартных игр (мультипликативной или аддитивной) люди меняют свою стратегию оценки риска, исходя:
- либо из оценки логарифмической полезности — для мультипликативной (красной) динамики игры,
- либо из оценки линейной полезности, для аддитивной (синей) динамики игры.
Этот эксперимент убедительно показал, что эволюция встроила в человека верную оценку рисков в плане выгодность/невыгодность. Куда более верную, чем навязывают ему современные экономические теории, заодно объясняя, что он — дурашка и не может по своей природной иррациональности сделать правильный выбор.
✔️ Так чем тогда экономика отличается от религии, если оказывает большее уважение к авторитету, чем к реальности?
Великий Л.Д.Ландау писал, что
науки делятся на естественные, неестественные и противоестественные.
Противоестественные — это те, что убеждают нас в представлениях, не соответствующих реальности.
Так не пора ли, наконец, перевести экономику и прочие науки, не признающие эргодичность в жизни людей, из класса противоестественных в класс неестественных наук, где они заняли бы свое достойное и заслуженное место.
Ведь это возможно. Единственное, что требуется, как пишет в декабрьской редакционной статье журнал Nature Physics, — выйти за рамки привычного «среднего мышления». И, похоже, что время для этого пришло: Time to move beyond average thinking.
И тогда, впервые за 300 лет, наш мир перестанет быть искаженным, а наши модели, наконец, совпадут с реальностью.
Credit: Pasquale Cirillo






Комментарии
Потому, как политизирована и идеологизирована задачей ставился не поиск истины а оправдание капитализма. Отказ от научности, заключающийся в отказе от философии и упоре на позитивизм привёл к подобному состоянию экономики и не только.
Автор интересно пишет но причинно-следственных связей не понял.
Адам Смит и Маркс, были.
А как тогда назвать Талеба? Ведь ответ простой- капитализм.
Автору срочно надо прочитать хотя-бы Маркса.
И что же Маркс писал про вероятность и эргодичность в экономике?
То-же самое, что и Галилей (и Аристотель , какой ужас...) -ничего.
А Маркса следует прочитать, для что-бы понять почему сложилась такая ситуация в социологии, психологии.
Да нет, тут про другое. Политэкономия описывала процессы в масштабе и их закономерности. А экономикс маскирует масштабные процессы с их кризисными составляющими и конечность рынков описанием мелких составляюших, их взаимодействие. Поэтому современные экономисты в большинстве своем непонимают что присходит вокруг. Я когда писал диплом по экономике по своей собственной организации мог показать ее как суперуспешной так и катящейся в пропасть в зависимости от выбранных показателей. Поэтому современная экономика это шаманство.
Слушай, моего кота пронесло... Прямо на коврик...
Для решения этой проблемы мне тоже Маркса почитать?
Читаю маркса, первый том, и убеждаюсь, - он абсолютный идиот. Не верите? Прочтите его размышленя о "цене" сюртука и 40 аршинов холста.
маркс, и его последователи - умственно недоразвитые. Точка.
Нет, Ваш авторитет равен нулю как и Ваше мнение. Даже мнение автора статьи ничтожно, доказать он ничего не смог, поскольку в тексте нет доказательств.
Никогда не опираюсь на авторитет. Всегда сужу по результату и факту дел. Поэтому изрекаю своё мнение таким.
маркс - ноль. "марксОиды" - умственно недоразвитые бедняжки. К счастью таких немного осталось. Вымрут. Динозавры с мамонтами в пример.
На дворе кризис предела расширения рынков и разделения труда (или падения эффективности капитала). И в чём были неправы Смит и Маркс?
"...И в чём были неправы Смит и Маркс?..."
- маркс "накуралесил",- в попытке описать "капитал", не придумав фундамента для расчётов. Остальная писанина - ни о чём. С начала "сюртуками" "мерил", а потом в "деньги" скатился.
Сравним с Энергометрологической Экономикой 2013 -2017 года, где описан фундамент всех видов расчёта, - энергия измеряемая в ждоуле. И метод, - опреденение первичной, вторичной энергоцен и их суммы - => которая есть итоговая цена. Абсолютно безальтернативная система домохозяйствования.
В лужу, прямо попой. Сами поищите в инете, чтоб не было сомнений. Рост идей марксизма. Особенно в америке.
...Особенно америке!? 😂😂😂 Там ещё есть "общество плоской земли" и церковь "макаронного монстра". -идеям маркса там самое место 😁😂😃
Вы сАми почитайте первый том его "капитала", особенно про сюртуки и холст как меру в экономике. Ну это же чистая клиника. Почитайте, прежде чем тут печатать отзывы об этом недоумке.
Мдяяя... Сколько умных графиков, и целая портянка текста. Однако после её прочтения я по прежнему хочу задать простой вопрос, и получить на него ПРОСТОЙ ответ.
Если вероятность выпадения орла и решки одинаковы, а при выйгрыше я зарабатываю больше, чем при теряю при проигрыше, то почему я неизбежно проигрываю? Ведь для этого монета должна чаще выпадать "неправильной" стороной, чем "правильной". То-ли монета в целом какая-то "неправильная", то-ли это какое-то МММ.
Специально для таких как вы был приведён пример с револьвером. И там тоже не понятно почему ожидаемый выигрыш равен 0?
Там понятно, потому что игрок навсегда выбывает при проигрыше. Но в случае с монеткой такого нет. Сравнение некорректно.
Там понятно, потому что игрок навсегда выбывает при проигрыше. Но в случае с монеткой такого нет. Сравнение некорректно.
На самом деле ваш вопрос некорректен. В случае подсчета орла и решки - просто так без нижнего и верхнего предела - у вас будет просто график выпадений болтать вниз-вверх и усредненная в очень отдаленной перспективе будет выглядеть в\как прямая линия в районе 50 на 50. В жизни же когда мы касаемся реальных вещей - то тут вступают в силу пределы. Вы не можете сделать свои средства ниже 1 доллара - если такова минимальная ставка в данной системе игр. Т.е. у вас получается - что нижний предел когда он доходит до ноля - умножает все предыдущие ваши успехи на этот самый ноль - и вы улетаете в подвал. А так как нижний предел - всегда меньше середины - то на графике линия всегда будет направлена вниз как и ваши финансы. На самом деле это хорошо согласуется с вероятностями в том смысле - что на бесконечно длинном отрезке вероятно любое событие - а значит пересечение как любой верхней так и любой нижней границы - только в жизни нижняя граница означает конец игры. И по нашим современным меркам - она ох как далека от бесконечности.
А, разве, в предложенной статье что-то говорится о "минимальной ставке" ?
Напротив:
То есть, играть можно бесконечно.
Но при бесконечности вероятности выпадения "орла" и "решки" равны. А, распределение выигрыша и проигрыша НЕ равно и смещено в сторону выигрыша.
Это означает, что даже из самой малой оставшейся суммы возможен рост, причём, натурально – рост в бесконечность.
Ну... если 2 х 2 = 4.
Возникает вполне закономерный вопрос: ОТКУДА у автора "ниспадающий график" ?
Быть может... монета – "левая" ? Или техника броска... специфичная?
Короче, ГДЕ формула, которая всё объясняет, в том числе и угол наклона ниспадающего графика?
Хитрость покажу на следующем примере.
У вас 100$.
Допустим вы один раз выйграли и один раз проиграли:
Выйграли 100$ + 50% = 150$
Проиграли 150$ - 40% = 90$
В итоге вы в минусе, хотя по идее вы должны навариться))
Это потому что база для плюс 50% (100$) ниже чем для минус 40 (150)
Премного благодарен.
Кстати, вне зависимости от "базы", если сначала проиграть, а потом выиграть – получатся всё те же... "тестикулы, только в профиль":
100$ - 40% = 60$
60$ + 50% = 90$
Чертовщина какая-то... "Выгода" – просто нагло лезет в глаза. Слюни в предвкушении сказочного богатства заляпали всю манишку. Перекос в сторону выигрыша очевиден, и тем не менее...
Потому что есть риск менеджмент, который гласит, что
при таких-то вероятностях выигрыш\проигрыш
и такой-то величине выигрыш\проигрыш
есть оптимальная доля ресурсов, которыми можно рисковать в каждой реализации.
Если эту долю значительно превысить или, хуже того, ставить все ресурсы на кон то проирыш неизбежен. Даже при положительном мат ожидании.
Ну то в статье чуть-чуть не догаврили, как в стиле любитель Росстата.
Да - как изучавший теорвер и знакомый с теорией игр могу подтвердить, что методы борьбы с неэргодичностью есть. Разбивай свои 100 баксов на доли и докладывай каждый раунд. Величину доли надо считать. Но это при известных вероятностях. Реальный рынок это условие не выполняет.
У меня есть подозрение, что та недоговоренность была во благо, поскольку реальный рынок не позволяет создать эргодичную стратегию принципиально, но объяснять почему так - несколько дольше.
Реальный рынок это игра с нулевой суммой (если не считать действия ФРС)...Поэтому его нельзя моделировать игрой со средой... Вы Big Short случаем не смотрели - там мне понравился момент когда два ботаника-постдока уже считают что стали мультимиллионерами потому, что "рыночная" стоимость (выигрыш объявлемый бесконечной средой) CDS Лемановых Братьев равна 30% (цифра условная - давно смотрел не помню), а ни закоротились при цене около 100%...Но покупателей нет...нет ликвидности - рыночная оценка в блумберге (результат объявлемый средой в нормальных условиях функционирования рынка ) это фикция - ты можешь заключить сделку, и окажется что из=за общей паники покупателя нет денег рассчитать - он в реальности с отрицательным капиталом на данный момент, как и большая часть спекулянтов...И за долю малую проблему берется решать Бред Пит - и находит компания с противоположной позицией - которая готова заплатить денег (причем полагаю вперед) но по цене 50%... И два ботаника соглашаются на синицу в руках...
https://ru.wikipedia.org/wiki/%D0%98%D0%B3%D1%80%D0%B0_%D0%BD%D0%B0_%D0%BF%D0%BE%D0%BD%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5_(%D1%84%D0%B8%D0%BB%D1%8C%D0%BC)
Интересны тут дейcтвия суперигрока - ФРС (или скажем шире расширенно- обощенного правительства), которая как раз в это время начала отошло от своих правил и начало QE , а праительства всех стран начали контрциклические программы стимулирования - в том числе рекапитализации/национализации банков - в принципе наверное соглашусь это нечестно по отношению к сотням миллионам вкладчиков - но это лучше, чем расстрелы забастовок ветеранов ...если мерять не в деньгах , а в крови
Ошибка в том, что там проценты ) Если бы речь шла о физической величине, а не о процентах, то всё бы работало согласно теории. Ну то есть, если бы мы брали условные 100 рублей и при решке получали 50 рублей,а при орле теряли 40 рублей - то на длинной дистанции это был бы выигрыш (при условии что можно временно уходить в минус). Но поскольку там проценты, то всё совсем не так) Просто рассмотрите две равновероятные и равночастотные итерации - первой выпадает решка, потом орёл и затем наоборот - сначала орёл потом решка. Что видим? Получится или 90 (если сначала приросли +50 %, потом от 150 потеряли 40 %) или снова 90 (сначала потеряли 40 % от сотни, получилось 60 - затем приросли половинкой). То есть, там проигрыш обеспечен ))) Не очень понятно, в чём новизна.
потому что есть критический проигрыш, который прерывает линейку. если ты допустим 3 раза вытянул неудачу, то тебе пофиг на то, что в будущем твои шансы увеличились, будущего не будет, потому что не на что играть. при 45% шансе на провал шанс проиграть всё до наступления выигрышной полосы выше, чем эти 10% повышенной вероятности удачи.
Потому что проценты нужно считать с конца. В случае выигрыша ваш капитал 150$, вы выиграли 33,33% от текущих 100% = 150$.
В случае проигрыша ваш капитал 60$, вы проиграли 66,66% от текущих 100% = 60$. 40/60 = 66.66%
Все проигрыши больше 1/3 (33,33%) ведут к проигрышу во временной перспективе.
чисто как пацан, который маленько умеет пользоваться калькулятором, ни разу не математик:
1) орел - 100*1.5 (+50%). 1/1.5 = 0.666
2) решка - 100*0.6 (-40%). 1/0.6 = 1.66666
получаем минимальные значения, необходимые для "обратимости" процессов.
А вот почему при выборке из толпы параллельных реальностей получаем выигрыш - не врублюсь пока.
Это как раз логично...
Кто-то проиграл всё, а кто-то выиграл в 1000 раз больше...
Пока-что выиграл...
А, все врубился, верхняя планка выигрыша не ограничена, тогда как проиграть можно не более 100 баксов.
Потому що автор манкирует.. У вас после каждого тура - не 100 долларов на руках как в эксперименте с ансамблем... Для того что бы было все также игру нужно модифицировать... Оставить капитальный счет и счет прибыи убытков, причем разрешен любой отрицательный баланс на счете прибылей/убытков...после игры вам денег не выдают и не вынуждают делать ставку на всесь остаток, а записывают на счет прибыли и убытков...Тогда да игра с положительным матожиданием по счету прибылей и убытков (и причем достаточно быстро)... А вероянтность убытков падает по гауссовому рапределению - очень быстро.
Теория вероятности крайне вычурная - в ней куча поводных парадоксов - которые кажутся проитворечиввм ежедневной интуиции... Например парадокс Монти-Холла... Он лежит в основе выигрышной стратегии в казино в блек-джек...Есть голивудский -фильм 21 - об этой реальной истории... Потом кчатит Торп (герой фильма) - стал одним из первых управляющих алгоритмического инвестиционного фонда
В примере игры, где орёл/решка это +50%/-40%, жадный видит (+50-40)/2=+5%, а реалист видит что, вероятность выигрыша и проигрыша одинаковы.
Для закрепления посмотрим на два шага, жадный считает (+125-10-10-64)/4=+10.25%, а реалист пугается что, в 75% случаев он в проигрыше.
Для временного ряда надо считать так, что в результате будет или 150%, или 60%, 1.5*0.6=0.9, т.е. усушка на 10% каждые 2 раунда.
Все дело в процентах.
Говоря простыми словами: последующий выигрыш 50% не покрывает предыдущего проигрыша в 40%: вначале проиграли 40$, осталось 60$, потом выигрыш принесёт 30$ и т.д.
Для игры в 0 необходимо играть по правилам: 66,67% выигрыша и 40% проигрыша.
Да камерад - дело в экспоненте ... Но при чем здесь эргодичность в упор понять не могу... Кроме того. Он рассматривает игру со средой - которая в любом количестве оплачивает выигрыш... Экономика - далеко не бесконечная среда - это сложная система с кучей обратных связей - например велфер - обеспечение минимума социальных благ, или прогрессивное налооблажение - кроме тог есть социальные бунты
Или для игры в плюс надо нарушить правила и всегда ставить одну сумму.
Не учтены варианты, монета встанет на ребро, повиснет в воздухе. Требую пилить гири дальше.
потому шо стратегия размещения 100% капитала в рискованные предприятия убыточна... ПРи чем здесь эргодичность вообще не понял...Но дело тут в оптимальном размещении капитала... Кстати оптимальная стратегия по Келли - тоже дает огромные просадки капитала (распределение убытков как обратный квадрат от величины убытка)... Чем если ставищь меньше Келли-оптимальной, то и просадки не такие жесткие... Короче в статьях по менеджменту фондов - это обсуждалось неоднократно... единственное - большей частью на английском языке...
https://en.wikipedia.org/wiki/Kelly_criterion
Потому что теряете от текущего баланса. Было 100 долларов, выиграли 50%, стало 150 долларов. Потом проиграли 40%, а это уже 60 долларов долой, осталось 90 долларов.
В таком случае автор привел надуманный и высосанный из пальца пример. Никто не играет на процент от текущего баланса. Все играют на ставку! А она не меняется.
Это как если бы в казино при каждом броске шарика на рулетке дилер подсчитывал не ваши фишки на столе, а ваши деньги в кармане.
Бред!
Без всяких формул и сделав несколько итерации понятно, что +50/-40 ведет к убыткам. Шанс выпадения орла или решки 50%. Если орлы и решки будут последовательно чередоваться (шанс на это очень велик), то получаем:
150 90 135 81 121,5 72,9
Редкий везунчик получит серию где + больше - , остальные разоряться.
А учебник прочитать?
У Найта (старая чикагская школа) в "Риск, неопределённость и прибыль" так обосновывается ценность демократии по сравнению с диктатом. Что никто не без греха, но диктат рано или поздно ошибается так, что всё летит к чертям, тогда как при демократии и сменяемости (при условии, что они реальные, а не постановочные) ошибки не имеют катастрофических последствий сколь угодно долго.
Там на одной из картинок портрет учёного Арроу. Так вот он доказал, что никакой "реальной" демократии существовать не может в принципе. А существует только четыре выбора: 1) диктатура, 2) общество с манипулируемыми выборами, 3) правящая клика, и 4) общество с отсутствием свободных выборов. Какой либо из этих элементов присутствует в любом обществе и это без вариантов. Вопрос только в том, какой из этих "недемократических" элементов доминирует.
Доказывать отсутствие или невозможность "реальной" демократии, наверное, было излишне.
Абсолютная диктатура точно также невозможна. Дело не в этом, практическая задача заключается в том, что можно представить себе два умозрительных полюса и расположить между ними реальные режимы правления. Какие-то из них будут ближе к одному полюсу, другие к - другому, все - в разной степени. И, исходя из этого, учитывать их устойчивость к разного рода ошибкам, включая дезу.
По идее - пока мягкие режимы найдут свою катастрофу, более жёсткие успеют сделать это два-три раза.
А вот такое утверждение математически доказанно не было. В отличие от.
Идея вполне рабочая. тут проблема в отсутствии симметрии времени. Она вполне прослеживается при рассмотрении элементарных физических задач, хотя уже в термодинамике неравновесных процессов это, очевидно, не так. Ну а что касается неравновесных нелинейных диссипативных систем время может быть посчитано однородными лишь в нулевом приближении. От того и возникают отличия в средних не только между ансамблевыми и временными, но и ансамблевыми, измеренными в разные моменты времени.
Только описываемый им случай вполне обратим по времени...но процесс мультипликативный а не аддитивный....возьмите логарифм - и получите случайное броуновское блуждание( совсем аддитивный процесс) с отрицтельнм матожиданием
Обратите t на -t и покажите, как Вы получите такую же минутную серию в обратном порядке. Я уверен, это так же просто, как и обратить неудачный опыт в русской рулетке.
И опять, не факт. Броуновское движение аддитивный процесс только в равновесной среде.То есть, где заведомо время однородно и обратимо.
обратите любую реализацию мартингала и вы получите тоже распределение вероятностей , что вперед, что назад... Если вы это не понимаете -- обратитесь к темодинамике - там куча таких эврогодических процессов ... которые спонтанно передводит из неравновесного маловерятного состояния с низкоэнтропией (по некотрой подсистеме) в равновесное состояние... причем полно физических реализаций - пример половина автомобильной камеры незакаченно - а вторая закаченна до избыточного даления в 2 атомсферы, после открытия соединяющего клавпана давленре установится на уровне 0,5 избыточного... причем процесс будет неравновесный, но вполне эргодический...
Я не зню в чем вы там уверены или не уверены - но броуновскре движение предельная ( в математическом смысле), реализация маркоского процесса (без памяти), которая хорошо реализуется в случае сложных систем, за характреное время,намного превышающее среднее время обмена энергией между составными частями ... именно о таком проу=цессе идеи речь при изучении идеальных рулеток и монет как в статье... В реальных условиях все сложнее - но не настолько что бы не использовать при некоторых мерах обеспечения типичности реальной выборки (как в казино - например никогда не задумывались для чего часть колоды колоды отрезают...первичная колода состоит из трех -четырех колод)
Это не означает обратимости. Система не пойдёт назад по той же фазовой траектории, ибо одному распределению соответствует очень даже много траекторий. Вопрос остаётся в силе: Вы можете хотя бы одну минутную серию провернуть назад в строго заданном порядке?
Условия не соблаговолите озвучить? Вероятно, в условиях умалчиваемых Вами частных допущений - да.
У Вас путаница между реальными явлениями, методами их описания и моделями - вариантах отражения реальности в рамках используемых методов. Например, реальное броуновское движение при наличии достаточных вычислительных мощностей принципиально вычисляется точно. Там нет ничего случайного. Вы путаете реальное содержание с методами исследования. Сами же методы, применимы лишь в очень ограниченных, заранее сформулированных, условиях.
Эргодичность не означает обратимость во времени... Эргодичность означает, что любая реализация процесса из выборки - типична... любая реализация процесса пройдет достаточно близко к усредненной по вероятностной мере функции выигрыша...
Обратить его назад можно - запрсто ...Но среди всех возможных реализаций, мера множества реализаций, в который баланс будет в точности равен начальному и балансу зафиксированном на каждом шаге при движении вперед по времени, будет стремится к 0 (в зависимости от номера шага на котром мы остановимся при движении вперед)...
>>>>>>Условия не соблаговолите озвучить?
Запросто
тут
https://ru.wikipedia.org/wiki/%D0%AD%D1%80%D0%B3%D0%BE%D0%B4%D0%B8%D1%87%D0%BD%D0%BE%D1%81%D1%82%D1%8C
или тут
https://en.wikipedia.org/wiki/Ergodicity
Приводимый в статье пример как раз и есть реализация марковского процесса и по теорема же маркова - он эрогдический
В нашем случае вероятностное простраство - это множество бесконечных бинарных строк (в оба конца причем бесконечных)...Топология - совпадение некоторого участка строк во всех бинарных строках открытого множества. Мера - 2^-l - длина совпадающего участка...Эрогодическое преобразование - сдвиг по времени на единицу вперед
>>>>>>Например, реальное броуновское движение при наличии достаточных вычислительных мощностей принципиально вычисляется точно.
Я те камерад больше скажу ........при наличии ручки и достаточного запаса бумаги, и некотрого времени в самом простейшем случае - задачи о блуждающем пьянице - движения по решетке решается вообще без применения компов (весьма хорошее упражнение чтобы понять что такое интеграл по путям для начинающих и как с его помощью выводится квантовмеханический пропагатор свободной частицы)
Страницы