Толчком к написанию этой статьи послужила другая статья – о числе 108 (https://cont.ws/@Sage/1374746). Дескать, и такое оно, и сякое, со всех сторон и круглое, и квадратное. Причём, одновременно!
С точки зрения человека, немного умеющего мыслить, – там одна вода. По сути, число 108 обладает только одним свойством: внутренний угол правильного пятиугольника в градусах равен 108. Всё остальное притянуто за уши. Причём, с усилием, достойным лучшего применения.
Пользуясь случаем, расскажу вам о своих изысканиях в этой области – в области поиска интересных свойств у чисел, чем я по молодости грешил. Да и сейчас мимо темы обычно не прохожу.
Однажды я узнал о существовании совершенных и сверхсовершенных чисел.
Совершенные числа – это такие числа, сумма всех собственных делителей которых равна самому числу.
Собственным делителем числа называется любой делитель числа, отличный от самого числа. У простых чисел только один собственный делитель – единица.
Примеры совершенных чисел: 6, 28, 496, 8128, 33 550 336, 8 589 869 056, и т.д.
Собственные делители числа 6: 1, 2, 3. Их сумма (1+2+3) равна 6, т.е. самому числу.
Сверхсовершенные числа в математической терминологии называются избыточными.
Избыточные (сверхсовершенные) числа – это числа, сумма всех собственных делителей которых больше самого числа.
Первым сверхсовершенным числом является число 12: 1 + 2 + 3 + 4 + 6 = 16 (>12)
Узнав о том, что существуют сверхсовершенные числа, я подумал: а что дальше? Полученное из 12-ти число 16 – какое оно? Несовершенное, совершенное или сверхсовершенное? Оказалось – недостаточно совершенное – сумма его собственных делителей равна 15. А у 15-ти – 9, и таким образом я получил последовательность:
12 16 15 9 4 3 1
Назвал эту последовательность «Жизнью числа», написал программу на Visual Basic и начал исследовать жизнь различных чисел. Нашёл немало интересного (как теперь знаю, уже известного, но тогда это были мои собственные открытия). Я нашёл, что существуют (в терминах современной математической теории):
Избыточные числа
Недостаточные числа
Слегка избыточные числа (квазисовершенные числа)
Слегка недостаточные числа
Дружественные числа
Полусовершенные числа
Кому интересно, могут почитать об этих числах в Википедии. Однако, не это не главное. Самым интересным для меня оказалось то, что у некоторых чисел – очень насыщенная внутренняя жизнь. Причём, порой ничем не примечательное число может иметь очень богатую внутреннюю жизнь.
В те времена, когда компьютеры были не так сильны, я не нашёл «конца» жизни у некоторых чисел. Сейчас вернулся к этой теме и просчитал их ещё раз. И даже сейчас я не нашёл конца у числа 720, которое в настоящий момент является рекордсменом по «длине жизни». Впрочем, по порядку.
12 – первое сверхсовершенное число.
Сверхсовершенные (избыточные) числа: 12, 18, 20, 24, 30, 36, 40, … 60, … 100, … 120, 126, 138, 140, … 180, … 360, … 720, …
Жизнь чисел бывает самой разной. Лучше всего её увидеть в графическом виде.
Жизнь числа 120 (максимум - 32 571)
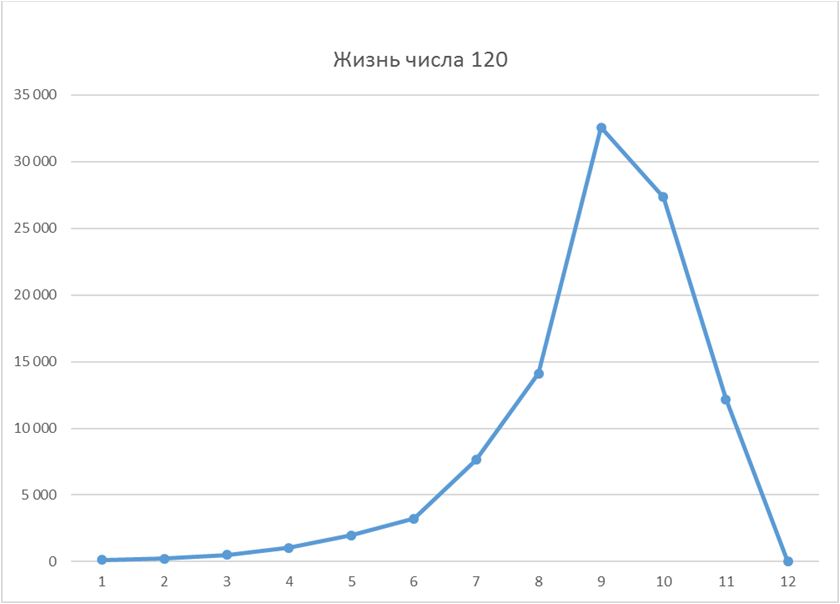
Жизнь числа 480 (максимум – 321 836)
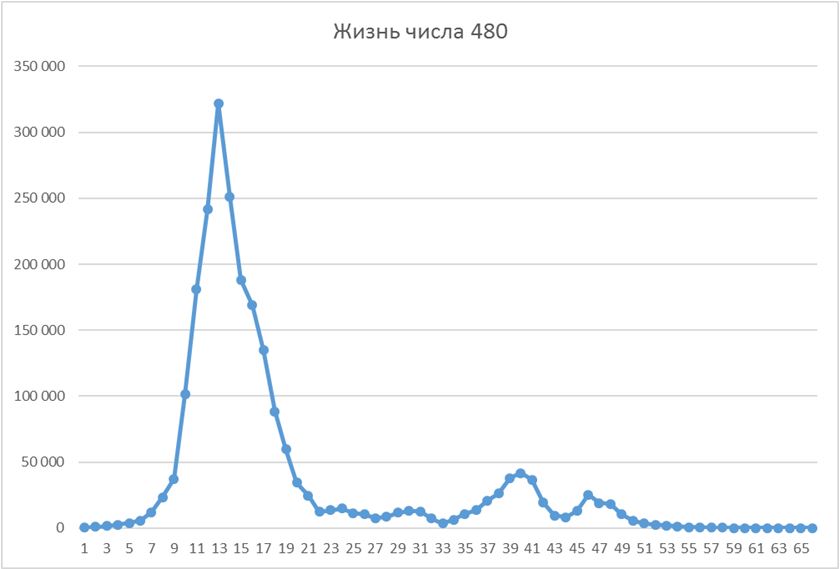
Жизнь числа 742 (максимум - 890)
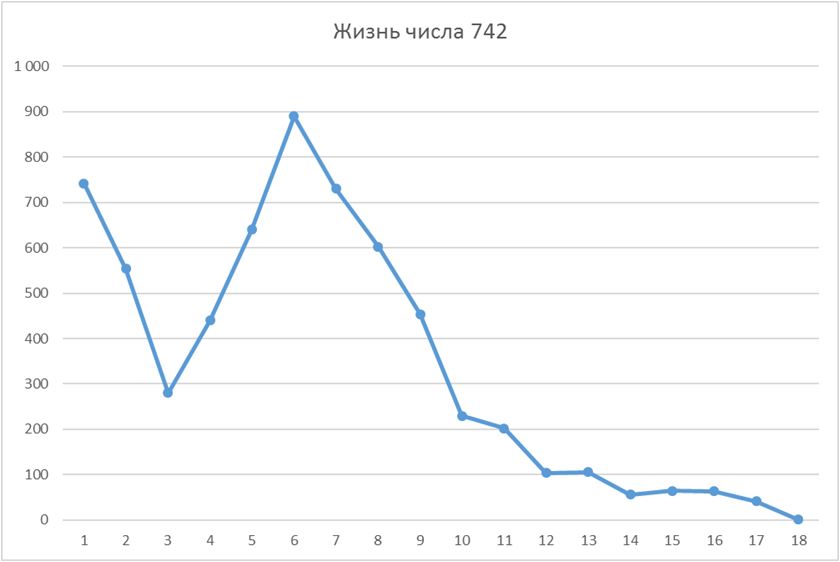
Жизнь числа 642 (в максимуме - 18 632 и 18 628)
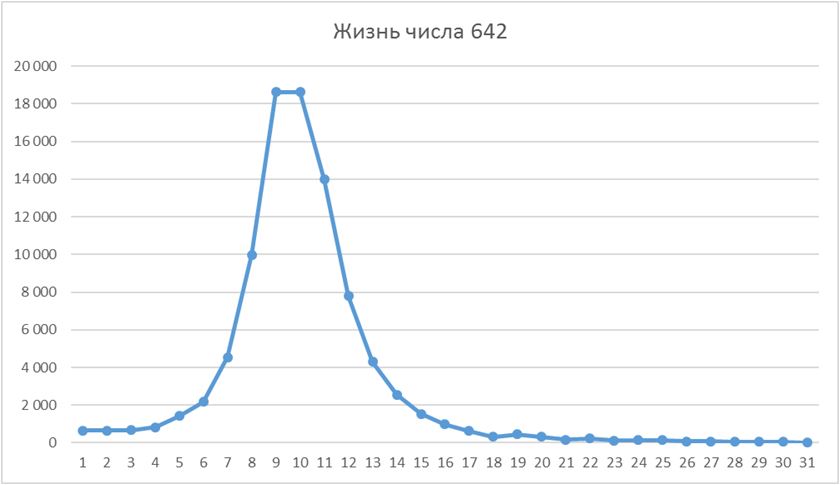
138 – наиболее сильно удивившее меня число. Его собственные делители ничем не примечательны: 1, 2, 3, 6, 23, 46, 69. Их сумма равна 150. А у 150-ти – 222. И т.д. Всю жизнь числа 138 мне удалось посчитать лишь недавно. Вот она:
138
150
222
234
312
528
960
2 088
3 762
5 598
6 570
10 746
13 254
13 830
19 434
20 886
21 606
25 098
26 742
26 754
40 446
63 234
77 406
110 754
171 486
253 458
295 740
647 748
1 077 612
1 467 588
1 956 812
2 109 796
1 889 486
953 914
668 966
353 578
176 792
254 128
308 832
502 104
753 216
1 240 176
2 422 288
2 697 920
3 727 264
3 655 076
2 760 844
2 100 740
2 310 856
2 455 544
3 212 776
3 751 064
3 282 196
2 723 020
3 035 684
2 299 240
2 988 440
5 297 320
8 325 080
11 222 920
15 359 480
19 199 440
28 875 608
25 266 172
19 406 148
26 552 604
40 541 052
54 202 884
72 270 540
147 793 668
228 408 732
348 957 876
508 132 204
404 465 636
303 708 376
290 504 024
312 058 216
294 959 384
290 622 016
286 081 174
151 737 434
75 868 720
108 199 856
101 437 396
76 247 552
76 099 654
42 387 146
21 679 318
12 752 594
7 278 382
3 660 794
1 855 066
927 536
932 464
1 013 592
1 546 008
2 425 752
5 084 088
8 436 192
13 709 064
20 563 656
33 082 104
57 142 536
99 483 384
245 978 376
487 384 824
745 600 776
1 118 401 224
1 677 601 896
2 538 372 504
4 119 772 776
8 030 724 504
14 097 017 496
21 148 436 904
40 381 357 656
60 572 036 544
100 039 354 704
179 931 895 322
94 685 963 278
51 399 021 218
28 358 080 762
18 046 051 430
17 396 081 338
8 698 040 672
8 426 226 964
6 319 670 230
5 422 685 354
3 217 383 766
1 739 126 474
996 366 646
636 221 402
318 217 798
195 756 362
101 900 794
54 202 694
49 799 866
24 930 374
17 971 642
11 130 830
8 904 682
4 913 018
3 126 502
1 574 810
1 473 382
736 694
541 162
312 470
249 994
127 286
69 898
34 952
34 708
26 038
13 994
7 000
11 720
14 740
19 532
16 588
18 692
14 026
7 016
6 154
3 674
2 374
1 190
1 402
704
820
944
916
694
350
394
200
265
59
1
В максимуме получено число 179 931 895 322. Длина жизни (длина полученной последовательности), включая само число – 178.
Скорость роста и падения значений ряда местами близко к экспоненциальному:
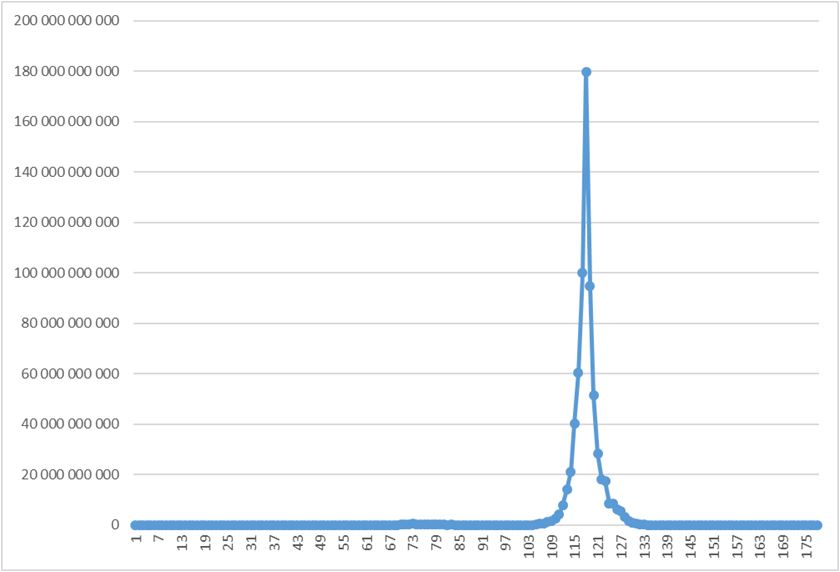
При этом небольшое утолщение в районе 70-ых значений – сам по себе тоже немаленький пик:
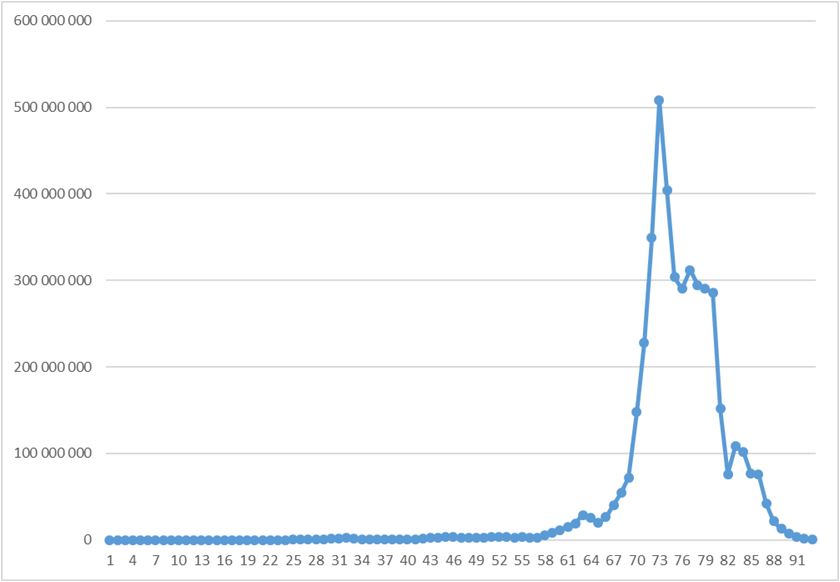
Чтобы сгладить перепады в жизни числа, возьмём логарифм полученных значений:
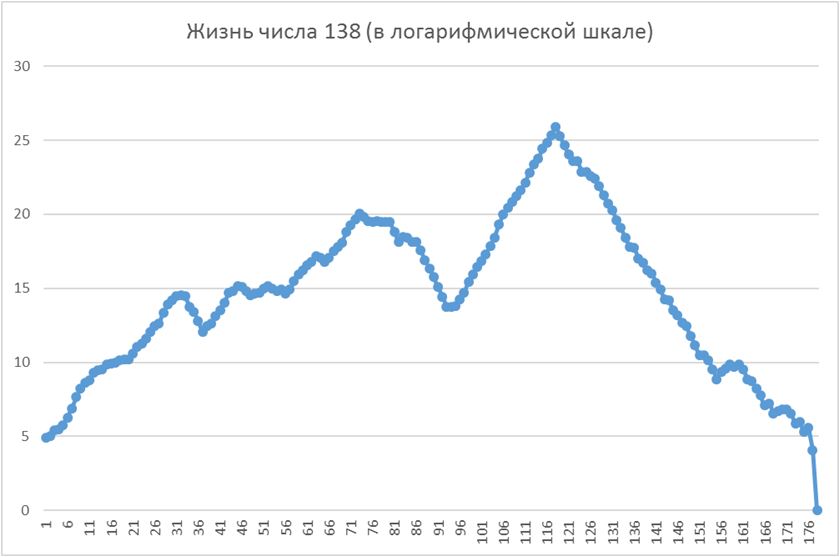
На участке от 93-го значения до максимального (значение 118) зависимость очень близка к экспоненциальной со степенью, местами близкой к 1,5. Т.е. отношение рядом стоящих чисел ряда почти точно равно 1,5. Самые близкие значения: 1,5000043767, 1,5000000805, 1,5000000536, 1,5002064735, 1,5000000015:
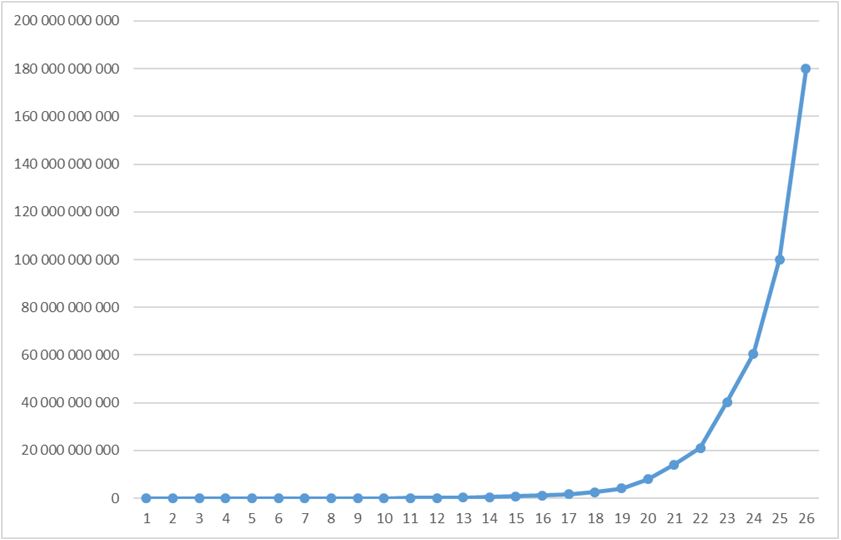
А на этапе падения кривой (перед вышеописанным взлётом, но не только там) степень близка к 0,5: 0,50296810, 0,50673870, 0,50000162.
Одной из самых длинных жизней из сравнительно небольших чисел обладает число 720 (360 х 2). Уже получено 96 значений и дальше дело застопорилось – в моём распоряжении нет компьютера/сервера под управлением Windows, на котором я мог бы запустить программу на месяц-другой в непрерывном режиме для нахождения всех значений. Если у кого есть возможность и желание помочь, пишите в личку – пришлю программу (exe-шник, с интерфейсом).
720
1 698
1 710
2 970
5 670
11 754
13 752
23 688
51 192
94 008
141 072
223 488
427 526
272 098
147 194
73 600
116 120
145 240
181 640
250 360
365 240
494 440
646 040
857 320
1 071 740
1 235 572
1 093 104
1 966 472
1 735 828
1 311 104
1 301 116
987 044
840 796
789 140
1 134 124
951 316
812 684
620 860
719 780
958 540
1 237 892
1 046 908
808 932
1 078 604
808 960
1 156 640
1 576 300
2 157 836
1 646 524
1 635 524
1 486 924
1 127 324
1 024 924
789 476
592 114
302 954
151 480
238 760
314 200
416 780
665 140
931 532
1 165 108
1 165 164
2 522 772
5 218 668
11 903 892
25 427 052
53 825 940
132 775 020
331 001 748
760 541 292
1 492 916 628
2 490 326 636
5 183 606 260
7 370 428 940
10 560 940 852
12 481 112 588
12 481 112 644
17 623 960 508
20 935 668 292
25 605 989 948
30 285 997 252
30 573 080 188
34 370 987 924
39 658 833 004
41 211 587 732
41 211 587 788
42 695 114 924
53 420 518 564
53 420 518 620
131 770 616 964
220 630 419 324
433 833 337 476
968 456 265 084
2 100 700 764 036
В связи с резким взлётом в конце найденного ряда, показывать просто график последовательности неинтересно. Логарифм смотрится лучше:
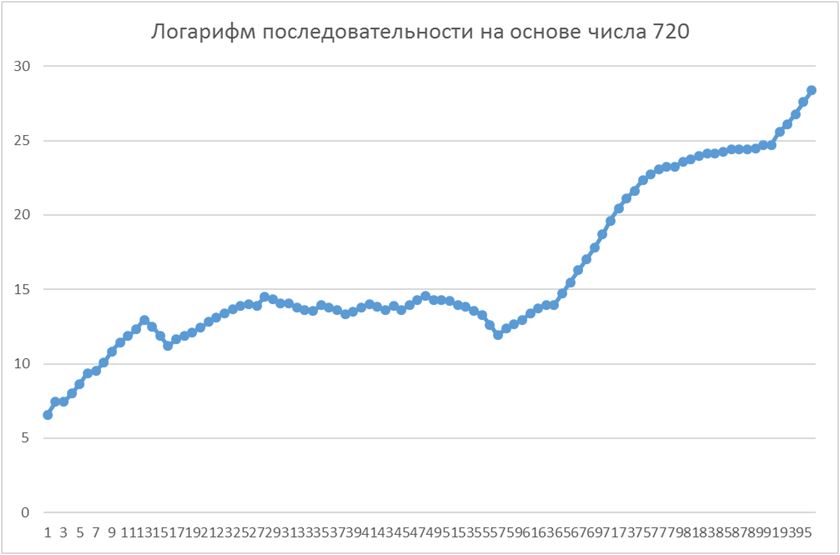
Жизни чисел бывают связаны не только «дружественными», а более сложными узами – числа, как ручьи, могут сливаться в реки. Например, числа 138, 150, 222, … через пару-тройку шагов сливаются в одну реку (получают идентичные последовательности):
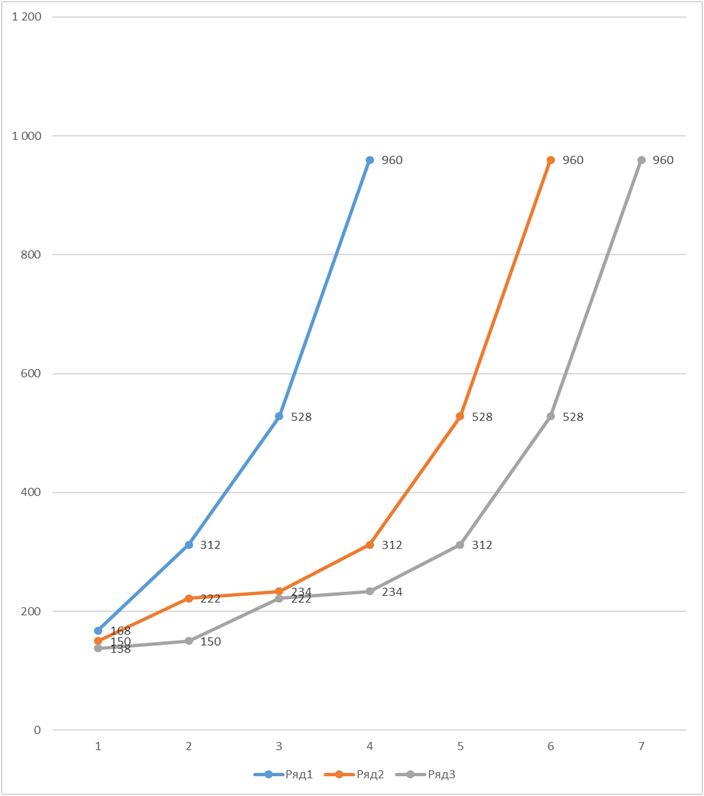
Таким образом, все числа, которые приходят к повторению последовательности других чисел, имеют разные корни, но общую судьбу. При этом основная линия судьбы принадлежит наименьшему числу. В данном примере – числу 138.
Ещё из интересного. Суммой делителей числа 720 является число 1698. Также это число является третьим в ряду, образованным от числа 1044. Но это же число является первым в ряду, образованным от чисел 1 326, 1 422 и 1 686. Т.е. сумма делителей чисел 720, 1 326, 1 422 и 1 686 равна 1698:
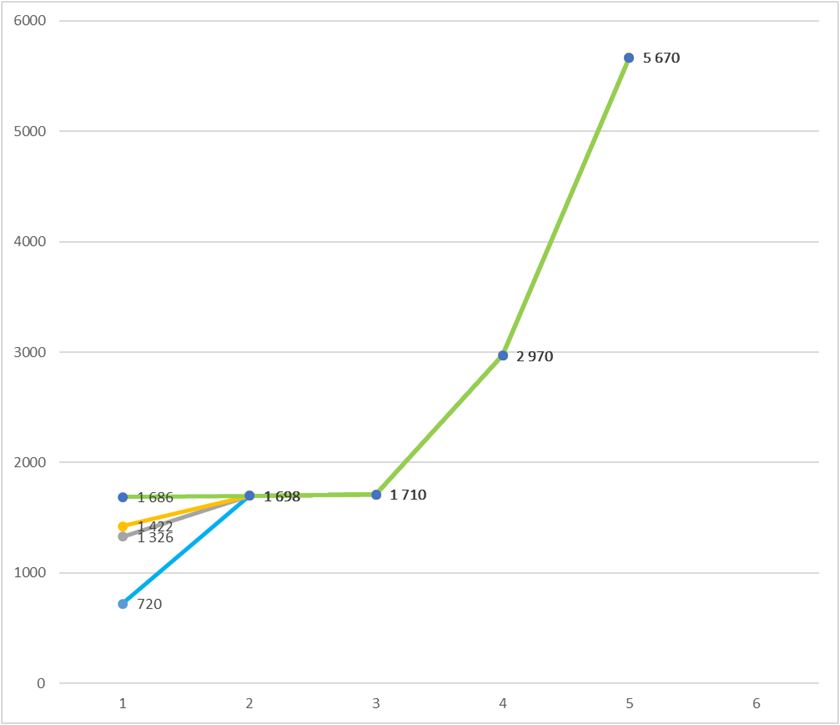
Уверен, что интересного в жизни чисел ещё немало. Я же только так, по верхам нахватал :)





Комментарии
и в чем физический смысл этого?
Физического - никакого :)
Вы не правы, физический смысл у этих свойств чисел вполне существует.. Когда-то, еще до Фейгенбаума, возможно, такое мнение бы могло бы иметь оправдание но с тех пор как Митчел Фейгенбаум первым в мире сыграл в вашу "игру".. это уже не так. Ваш опыт это частный случай итерированной последовательности. Разница в том, что Фейгенбаум работал с логистическим уравнением и вывел свой универсум для унимодальных отображений. Ваше же отображение куда заковыристее.. Вообще все что касается теории чисел это жесть жестокая. Сумма делителей как функция от числа это заковыристо. И все же ваши результаты очень похожи на класику, может быть даже к вашим опытам тоже можно прикрутить ренормгрупповой анализ.
Что же до физического смысла, то природа использует аналогичные вашему алгоритмы для построения фрактальных форм.. Возможно ваш вариант служит алгоритмическим основанием для построения чьего-нибудь фасеточного глаза или рисунка на крыльях :) , а может поверхности какого-нибудь неживого предмета..
Верно. Дополню, пожалуй. Наш мир структурирован или, говоря другими словами, представляет из себя систему, состоящую из элементов. На каждом уровне мироздания есть своя структура. Например, протон состоит из кварков, антикварков и глюонов.
Из чего состоят кварки? Из струн. Счётное ли это число? Счётное. Сколько струн уместится в объёме кварка? Много.
На каком уровне элементы системы можно считать неразличимыми друг от друга? Начиная с уровня атомов и далее вниз по шкале масштабов. Да, один электрон нельзя отличить от другого, точно так же, как и протоны, и нейтроны, и кварки, и струны. Ну вот, чем вам не числа? Натуральные числа.
Сюда же относится и задача по нахождению "кирпича Эйлера" - прямоугольного параллелепипеда, у которого все рёбра и диагонали являются целыми числами. Дело в том, что у квадрата с длиной стороны равной 1, диагональ будет равна √2, то есть, не целому числу. Ага, мягко говоря, не целому.
Число состояний системы, опять же, является целым числом. Правда, размерность пространства может быть дробной. И даже трансцендентной.)
Я так понимаю, под дробной размерностью пространства понимается фрактальная размерность? Потому что реальная может быть только целочисленной.
Более того, если не уходить далеко от здравого смысла, то ещё Эренфест в статье «Каким образом в фундаментальных законах физики проявляется то, что пространство имеет три измерения?» более века назад доказал, что размерность пространства равна трём.
Да. Это можно легко представить себе, если разбить окружающее нас пространство на элементарные кубики с длиной ребра равной 1. Теперь вписываем в каждый кубик по сфере. Таким образом, диаметр сферы также будет равен 1.
Сфера будет касаться соседних сфер. Да, будет касаться в одной точке. Кстати, можете по ходу дела решить задачку о наиболее плотной упаковке сфер. В случае с кубиками сфера будет касаться 6-ти соседних сфер. Столько же соседних окружностей будет касаться и окружность, вписанная в правильный 6-угольник. Если окружность вписать в квадрат, тогда она будет касаться 4-х соседних окружностей. Но это уже мы переходим от 3-мерного пространства к 2-мерной плоскости.
Да, так вот, если считать единичную сферу наименьшим элементарным объёмом, то между сферами остаётся некоторый объём, недоступный нам. Таким образом, размерность нашего мира становится фрактальной и меньше 3. Причём, она не будет постоянной, а будет постоянно колебаться между 2 и 3, в зависимости от плотности упаковки единичных сфер.
Ну а теперь проделаем совсем уж простую операцию. Заменим сферы на 10-мерные гиперсферы и получим более-менее реалистичную картинку нашего мира.)
Я, конечно, не математик, да и не физик, поэтому на равных с Вами не могу рассуждать об этих материях. Однако фишку про 10-11-мерные пространства знаю. Она в том, что если ты имеешь какую-либо проблему в теории, добавь измерений. С 10-ю - 11-ю измерениями теория начинает сходится с наблюдаемой действительностью :)
Но на число измерений и, вообще, строение мира у меня свой взгляд: http://kivankov.ru/articles/dmm.pdf
Вообще-то, все эти квантовые эффекты, типа корпускулярно-волнового дуализма, совершенно естественным образом выводятся из условия дискретности нашего мира. Попробуйте создать свой собственный мир. Попробуйте, попробуйте!
Возьмите листок в клеточку. Это квантово-механическое поле. Ну вот, а дальнейшее совсем уж просто. Во-первых, у вас получится некоторая предельная скорость передачи взаимодействия от клеточки к клеточке. Во-вторых, у вас сразу же получается предельная максимально возможная частота волны, равная обратной величине её минимально возможной длины. Длина же эта будет равна 2 клеточкам.
Ну и да, вы сразу же получаете и минимально возможную амплитуду волны, равную 1 клеточке. Но это уже, так сказать, дополнительным и приятным бонусом.
Ну а теперь попробуйте запустить круговую волну с единичной амплитудой, равной 1 клеточке. Что мы будем наблюдать? Во-первых, в отличии от обычной круговой волны на поверхности воды, наша волна будет распространяться без потери энергии, то есть, с постоянной и не уменьшающейся амплитудой. Просто потому, что меньшей амплитуды быть не может.
Кстати, вот вам и объяснение чудесных свойств квантово-механического поля.
Вернёмся к нашей волне. Если у обычной волны будут колебаться все поплавки по окружности, то у нашей - только один, выбранный случайным образом. Зато амплитуда его колебаний будет одной и той же, независимо от расстояния до источника волны.
И эта модель блестяще подтверждается экспериментом. Всегда срабатывает только один детектор. И срабатывает в момент прохождения через него фронта волны. Ни раньше, ни позже.
Что же касается дополнительных измерений, то попробуйте обойтись без них. Если вы полагаете, что это позволит сделать модель более простой, то... в добрый путь! )
Я своё слово в этой сфере уже сказал (http://kivankov.ru/articles/dmm.pdf) и даже в МГУ на семинарах доклады делал. Не все д.ф-м.н. со мной были согласны, но "аплодировали стоя" :)
Интересно. Иду писать считалку)
Не обижайтесь, но программист из вас вышел не очень.
Вот консольная программа для счета таких последовательностей (сумма всех множителей), и под спойлером результат для 720:
Вообще ни разу не программист - это единственная, написанная мной полноценная программа :)
Большое спасибо!
Del
Извините, не хочу скачивать и запускать данную программу, но мне интересны две вещи:
1. Какой язык.
2. Какой тип данных использовали для расчетов? 8-ми битного целочисленного long/ulong хватило? Просто числа в последовательности какие-то больно огромные, явно в 32-бита не влезут.
c++, long long.
Вообще можно было бы слинковаться с GMP и использовать длинную арифметику и нахождение множителей оттуда, но хватило и простого c++.
Загуглил, выходит это просто 64-х битный целочисленный тип. Спасибо.
Инт64 давно присутствует. Но не доказать, что его всегда хватит )
Забавно... а Вы пробовали посмотреть на жизнь иррационального числа,... какого нибудь корень из -1?
Иррациональное число не имеет целочисленных делителей, его таким подходом исследовать не получится.
Зато прыжки по комплексным с подсчётом шага вылета дают двухмерные красоты
осталось понять, можно ли это применить для чего-то полезного
Угу ,новые биткойны придумать. ;)))
Мне не удалось, но это не значит, что этому никогда не бывать :)
Считаю число Пи самым загадочным числом.....
Любой кто предоставит его счисление... будет с Нобелевкой
Сумма обычных дробей подойдёт? )))
Я про счисление говорил.
Ну как бы логика подсказывает, что "жизнь числа" идет ровно до первого встреченного простого числа. Интересно, существуют ли числа с потенциально бесконечной жизнью.
Всё верно, предпоследнее число в последовательности - простое. Но вот то, как числа к нему приходят - это интересно. И - по разному. Но чем больше число, тем чаще его "судьба" повторяет уже бывшие, меньшие числа. Это, кстати, тоже, интересная ветвь в исследовании, но это уже - для других.
Бесконечной жизни у конечного числа быть, думаю, не может. Если нечто исчислимо, следовательно, оно конечно. И всё, что можно вычислить из конечного, - тоже конечно.
Ну длина иррациональных чисел бесконечна же и ничего. Если вы планируете продолжать ваши исследования по этому вопросу, то думаю интересным был бы вопрос о том, какие числа чаще всего встречаются в последовательностях. Ну типа 2 - 100 раз, 545 - 1342 раза, на заданном диапазоне числе (например от 2 до 10 000). Вообще, успехов вам в вашем бесполезном, но явно забавном деле!
P.S.: Бесконечной она кстати может быть при образовании "числовых петель" в цепочках жизни.
1. Делители - это не множители. Их не бывает повторяющихся.
2. Тему я давно "закрыл"и продолжать не планирую. Сейчас просто вытащил на свет божий :)
3. Числовых петель в данном случае также быть не может. Бывают просто совершенные числа, которые сами по себе и дают "петлю". Но дают её сразу. В глубине последовательностей такого уже быть не может.
P.S. Да, это исследование тянет на шнобнлевку :)
25, 6, 6, 6, ...
Перспективный чат детектед! Сим повелеваю - внести запись в реестр самых обсуждаемых за последние 4 часа.
А ещё на хоккейных клюшках у Медведя (из мультфильма "Маша и Медведь") написаны даты Ледового Побоища и Куликовской Битвы.
занимательно!