Проходим через рамку маталлодетектора.
Телефоны оставляем. За вами наблюдают наблюдатели тд и тп. В общем полный фарш))
Есть ручка и бумага и больше ничего.
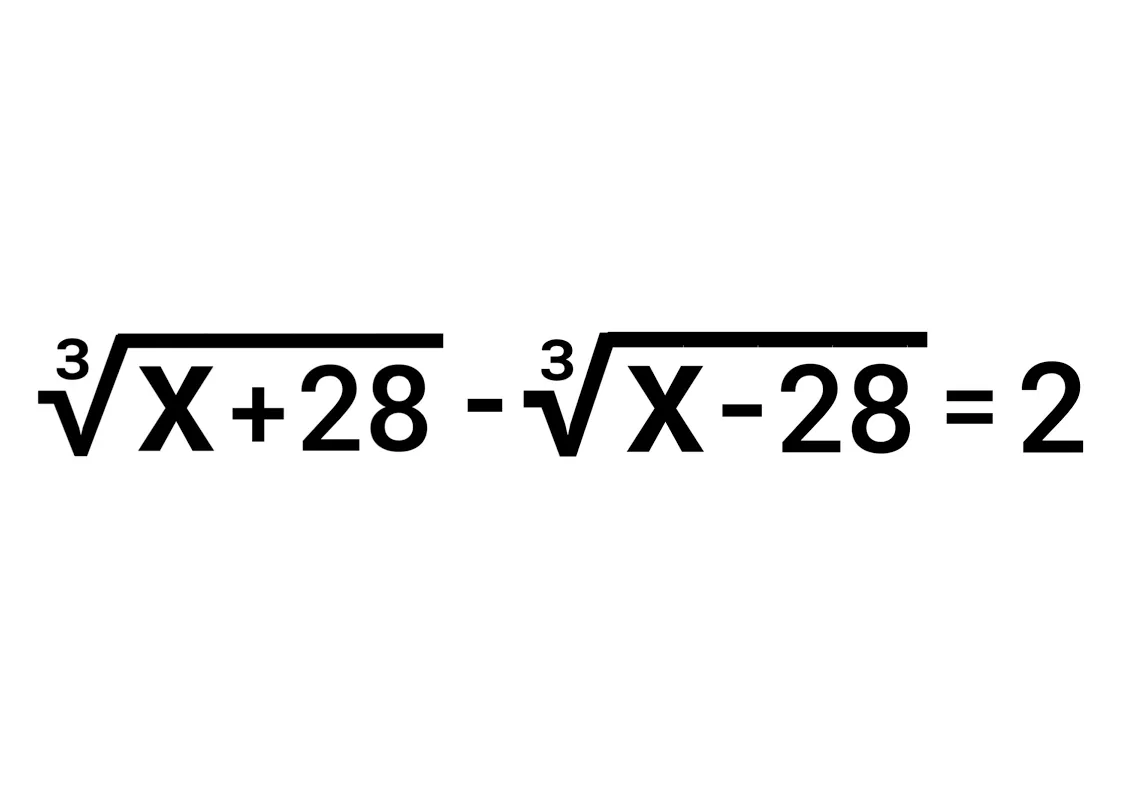
Люди не понимают хорошего отношения.
Для тех кто любит решать перебором немного другие условия))
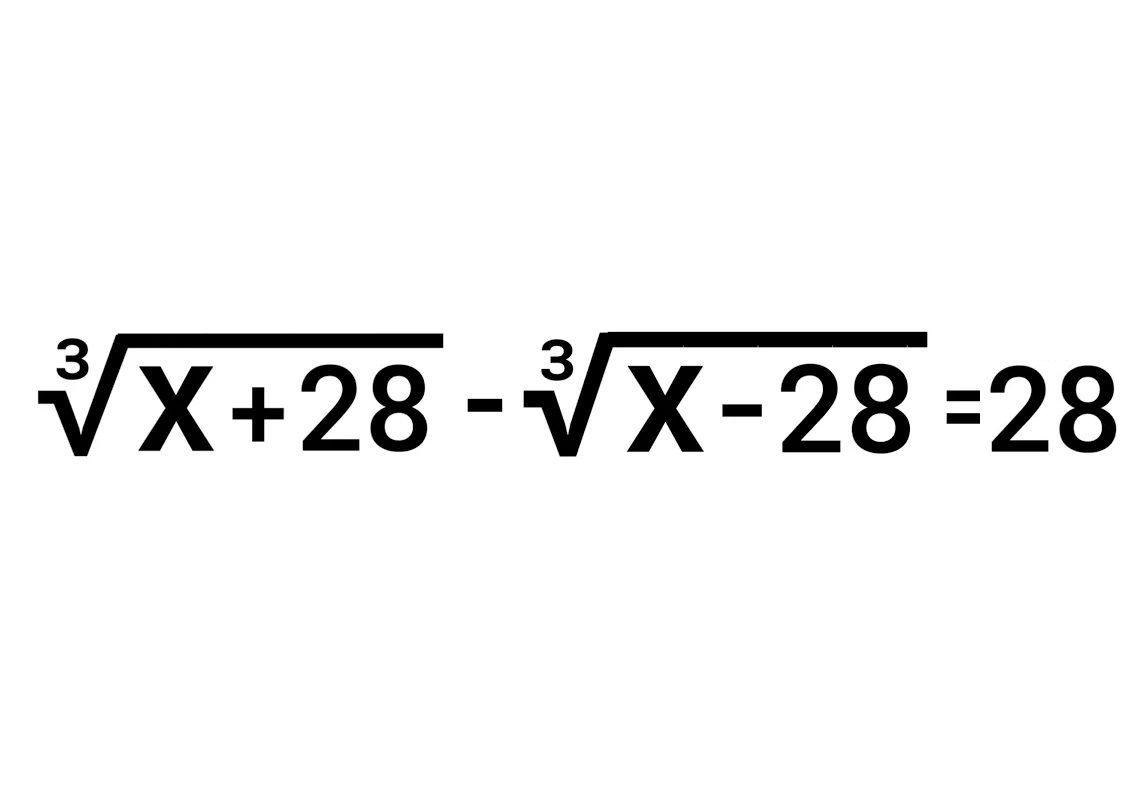
Комментарии
што и без мозгоф?
вам да
спс
В Вашей формулировке решений у обеих задач бесконечное количество.
x - 28 = n^3
x+28 = (n+28)^3
n ≥ 1 любое
мда...
осталось вам решить систему и доказать это))
Х=36. Перебором.
решайте перебором второй вариант))
а остальные корни?
28=36-8.
И что дальше? Также можем подобрать, можем слагаемые посчитать.
остальные корни
Мы х ищем или что?
ну попробуйте найти игрек))
х=36.....выводим из-под корня, переносим, считаем....кубический корень тяжко без куклькулятора, но то так ...
что вы там выносите из под корня?
а остальные корни?
Должно быть простейшее, значит перебором.
решите 2й вариант
Первый пример за 20 секунд решил. 4-2=2, дальше детали, х=36.
.
Не то
.
А нафига ? В чём практический смысл ?
На это же давно дан ответ.
А в чём практический смысл спортсмену в спортзале поднимать штангу? Ему где-нибудь в жизни пригодится поднимать штангу? Нет, не пригодится, но вот сила, которую он приобретает в спортзале, ему много где в жизни понадобится. С математикой так же.
Про период полураспада знаний не слышали, не?
А у спортсмена это цель - поднятие тяжестей.
У всех поголовно? Конечно нет. Мы например - просто баловство, развлечение, чтобы не скучно. Автор имеет свою цель. А школьникам тоже баловство, но мы помним, что всё молодое (котята, собачки, медвежата, козлята... ) развивается в игре. Так и человек.
) развивается в игре. Так и человек.
Весы сломались, но у вас есть упаковочные кубические коробки разного размера, с шагом в 2 единицы между размерами. А вам вдруг потребовалось отмерить 56 условно литров дефицитной гречки покупателю. Вопрос какую коробку вложить в другую, чтобы оставшийся дельта-объём можно было заполнить именно 56 литрами гречки. Практичней некуда
Ну может быть я глуп, но этого не боюсь.
Вычитаемое приравниваем к 56, возводим обе части слева и справа в куб
останется х+28=56*56*56
х=56*56*56-28
Первый: 36, -36.
Второй не имеет вещественных корней.
В авторе чувствуется рука человека, впервые увидевшего задачу внутришкольной олимпиады по математике для 8 класса
Вроде в 8 квадратные уравнения проходят...
Наверное, автор помогает своему ребенку готовиться к ЕГЭ. Ну и впечатлился.
Квадратные уравнения, кажется, проходили в четвертом или пятом классе школы.
Квадратные уравнения и метод замены переменных - 8 класс, 2-я четверть. Это у нас в РБ. Почему знаю? Только старший проходил.
Решать через квадратные уравнения 28^3, без калькулятора - такое себе удовольствие. А корень из дискриминанта?
йес
Подстановка t**3=x+28 позволяет преобразовать оба этих уравнения в обычное квадратное уравнение.
Переносим (x-28)^{1/3} в правую часть и возводим в куб. Обозначаем y = (x-28)^{1/3}. Для у получаем квадратное уравнение. Дальше по школьной программе.
1) x1=36, x2=-36
2) Уравнение не имеет действительных корней
Перспективный чат детектед! Сим повелеваю - внести запись в реестр самых обсуждаемых за последние 4 часа.
Если не ошибаюсь, то это тот ТС, который не признает других решений, кроме того, которое ему известно, поэтому только ответы
1. -36, +36
2. Решения не имеет.
Пример на знание одной - единственной формулы: (x-y)*(x2+xy+y2) = x3-y3. Для пользователей старше 20 проверяет не математические навыки, а память. Нехорошо так над людьми шутить.
А перебор зачем? Это же простое уравнение. Сейчас ЕГЭ стало такое примитивное, или школьники тупые?
Родители...
Некоторые
Я офигеваю, как много людей ведутся на тупое "а вам слабо"?
Математика - это то, чему научили. Или не научили.
.
Двойка это ноль(который есть) в кубе,
1 - (-1) =2, при х =0.
Второй пример без решения.
36, -36. Достаточно просто
А в чём проблема? Возводим в куб, а дальше элементарнейшие выкладки.
Решением уравнения (x+a)1/3 - (x-a)1/3 = b является x = ± (a2 + [(2a - b3) / 3b]3)1/2
Подстановка (a,b) = (28; 2) дает x=±36.
Один корень перенести за равенство, поменяв знак, возвести в куб обе части. При эйтом уйдёт одно основание корня далее заменим второй основание буквой Y и увидим что уравнение сводится к квадратному, которое решается по теореме виета. Проверяем корни на нашей замене и уже находим нужный