Сказать, что люди «не разбираются» в вопросах вероятности, было бы упрощением и подлостью. Теория вероятности — это деликатная отрасль современной математики, наполненная парадоксами. Даже элементарная проблема может порою сбить с толку хладнокровного эксперта. Высмеивать людей за их неудачные вероятностные оценки — это все равно, что называть их плохими пернатыми, осуждать их за неспособность глотать океаны или упрекать за отсутствие огнеупорности.
Нет, было бы справедливее сказать, что люди вообще ужасно плохи в вопросах вероятности.
В своих психологических исследованиях Дэниел Канеман и Амос Тверски обнаружили, что люди предвзяты и совершают систематические ошибки по отношению к случайным событиям. Люди постоянно переоценивают вероятности редких событий и недооценивают вероятности того, что случится почти наверняка.
Ну и что из этого? Я имею в виду, реальны ли вообще вероятности? Мы же не проводим свою жизнь в поисках интеллектуальных инструментов, которые могли бы дать нам хоть какую-то опору в клубящихся миазмах неопределенности, которые постоянно нас окружают…
Тем не менее, на всякий случай: эта глава представляет собой доступное руководство о том, как разные люди думают о неопределенности. То, что это сложно, еще не означает, что мы не можем извлечь из этого удовольствие.
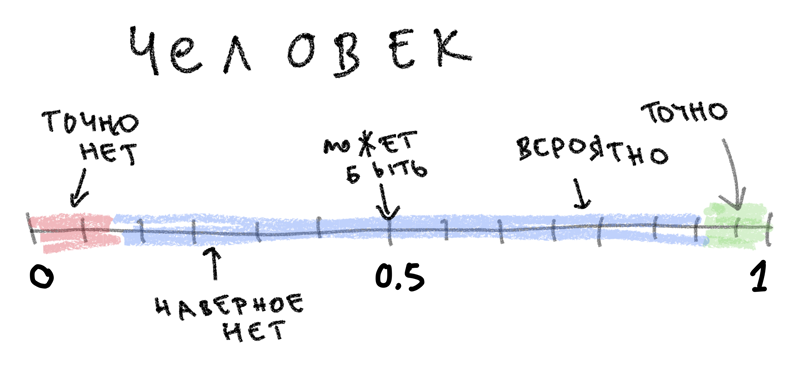
Привет! Вы — человек. У вас есть два глаза, нос и чувства. Вы мечтаете, смеетесь и ходите в туалет, не обязательно в таком порядке.
Кроме того, вы живете в мире, где нет ничего определенного.
Возьмем простой факт: сколько планет в вашей Солнечной системе? Сейчас вы говорите «восемь». С 1930 по начало 2006 года вы ответили «девять» (считая Плутон). В 1850-х годах вы написали учебники, в которых было перечислено двенадцать: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун, Церера, Паллада, Юнона и Веста. (Теперь вы называете последние четыре «астероидами».) В 360 г. до н.э. вы назвали семь: Меркурий, Венеру, Марс, Юпитер, Сатурн, Луну и Солнце. (Теперь вы называете последние два «луной» и «солнцем».)
Вы продолжаете менять свое мнение по мере появления новых данных и новых теорий. И что характерно: когда дело доходит до знаний, у вас есть много хороших идей, но нет абсолютной уверенности. Учителя, учёные, политики, даже ваши органы чувств — любой из них может вас обмануть, и вы это знаете.
Вероятность — это язык для выражения уровня вашей уверенности. Он позволяет вам дать количественную оценку для случаев, когда вы что-то знаете; или когда вы сомневаетесь в том что знаете; или когда вы знаете в чем сомневаетесь; выражая эти нюансы вашей уверенности ясным и четким языком. По крайней мере, таков замысел…
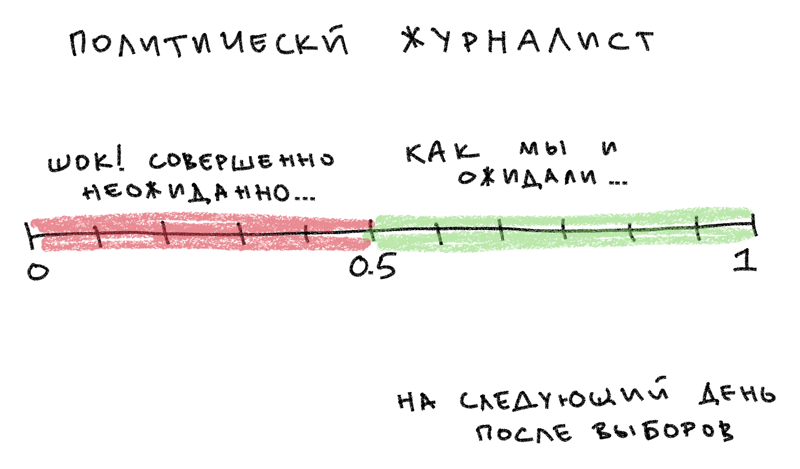
Привет! Вы политический журналист. Вы пишете о приближающихся выборах. Вы пишете о том, как проходят выборы. Иногда, по особенным дням, вы пишете о политике и власти.
Кроме того, кажется, больше всего вас занимают маловероятные исходы.
Это не всегда было так. Когда-то выборы воспринимались вами как волшебные моменты, когда возможно все. Вы преуменьшали наиболее вероятный исход, чтобы создать интригу и создать впечатление, будто каждая гонка была выиграна в последнюю секунду… нажатием на красную кнопку… в падении. В ночь выборов 2004 года, когда Джордж Буш лидировал в Огайо с преимуществом в 100 000 голосов, а для подсчета осталось едва ли 100 000, вы говорили, что баланс «слишком деликатен, чтобы можно было назвать победителя». Когда в 2012 году вероятностные модели дали Бараку Обаме 90% шанс на победу, вы назвали гонку «лотереей».
Затем 2016 год превратил ваш мир в перевернутый ананасовый торт. Дональд Трамп победил Хиллари Клинтон. Проснувшись на следующий день, вы почувствовали, что столкнулись с квантовой сингулярностью, столь же невероятной, как, скажем, кролик, материализовавшийся из воздуха. Но для специалиста по теории вероятностей Нейта Сильвера и многих его коллег результат выборов был лишь умеренным сюрпризом, с вероятностью 1/3 — все равно что бросить игральную кость, и получить 5 или 6.
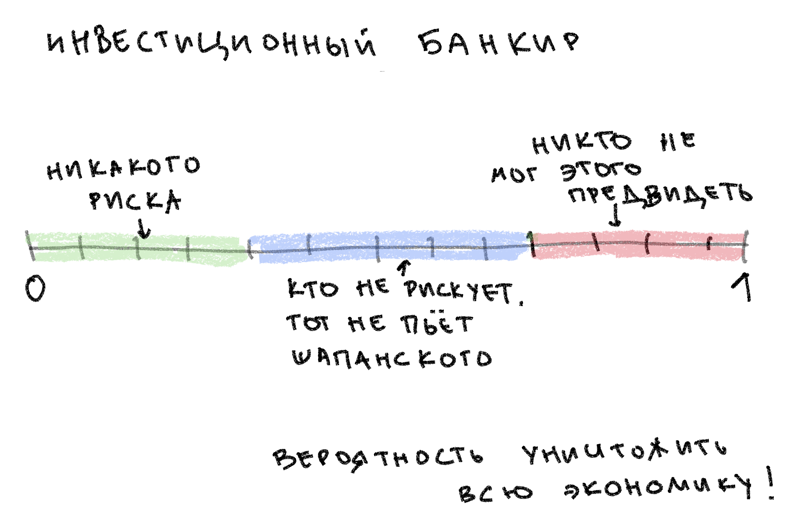
Привет! Вы - инвестиционный банкир. Вы работаете с инвестициями. Вы инвестируете в банки. И ваши костюмы стоят дороже моей машины.
Ещё в 1970-х ваша работа была довольно скучной. Вы были сродни засасывающей деньги воронке, переливая деньги в "акции" (то есть, в доли компаний) или "облигации" (то есть, в доли долга). Акции были захватывающими; облигации - скучными. Вы были живой облигацией.
Теперь ваша работа захватывающа, как американские горки, не прошедшие проверку безопасности. Начиная с 1970-х и 1980-х вы начали изобретать сложные финансовые инструменты, которые никто полностью не понимает, особенно государственные регуляторы. Иногда эти изобретения приносят тебе большие бонусы. Иногда они заставляют вашу столетнюю фирму обанкротиться, оставляя огромный кратер в экономике, как будто ударил астероид, уничтожающий динозавров. Волнующие времена!
Честно говоря, распределение капитала - довольно важная работа в капитализме и потенциально создает богатства. Вас раздражает, когда насмешливые учителя математики пренебрежительно отзываются о вашей профессии. Если это так, уделите минутку, чтобы посчитать, во сколько раз ваша зарплата превышает зарплату насмешливых учителей математики, и я думаю, у вас сразу поднимется настроение.
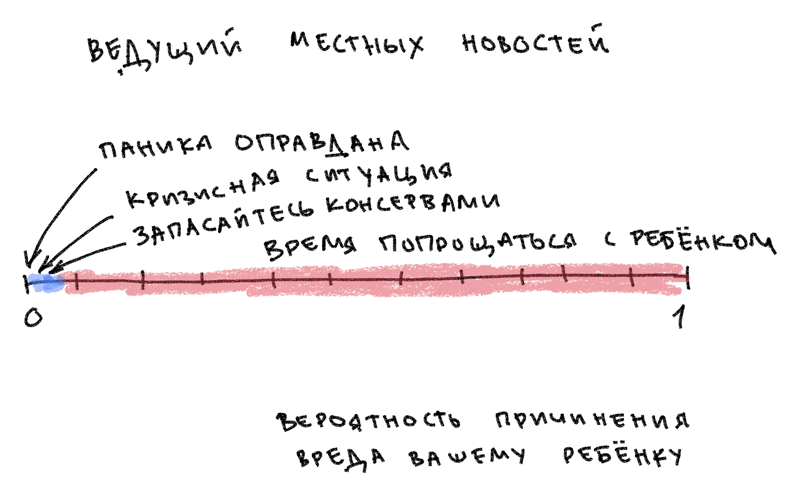
Здравствуйте! Вы ведущий местных новостей. У вас великолепные волосы, четкое произношение и долгая история фальшивой болтовни с вашим со-ведущим.
Также, вы одержимы очень маловероятными событиями.
Вам нравится сообщать о мрачных опасностях. Местные убийства. Воздушные канцерогены. Дефектные игрушки, которые прикрепляются к пухлым щекам вашего ребенка как существо из фильма "Чужой". Вы делаете это якобы для информирования аудитории. Но будьте честны. Вы делаете это, чтобы захватить их внимание. Если бы вы хотели улучшить осведомленность о статистических опасностях для детей, вы бы предупредили о бытовых несчастных случаях, связанных с оружием или бассейнами. Вместо этого, вы рисуете яркие картины, в которых единственная опасность более насущная, чем похищение, это нападения крокодилов. Вы знаете, что мы не можем отвести глаз от таких ужасов - особенно когда они смягчаются вашей фальшивой болтовней в студии.
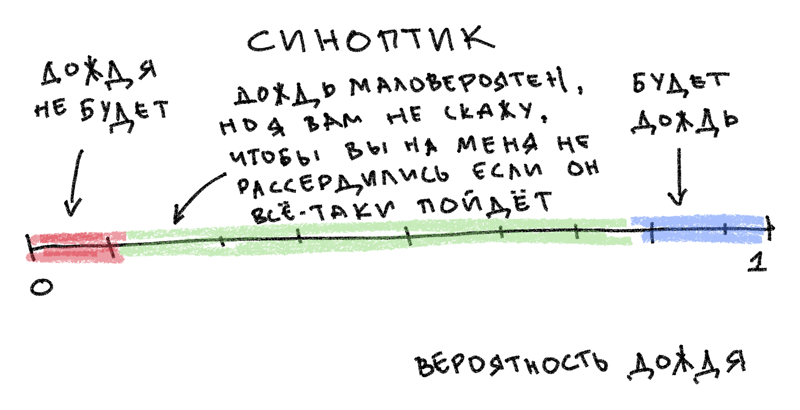
Здравствуйте! Вы - синоптик. Телевизионный толкователь облаков. Вы жестикулируете с убеждением и заканчиваете каждое выступление словами: "А теперь назад в студию.”
Также вы искажаете вероятности, чтобы люди не злились на вас.
Конечно, вы стараетесь быть честными. Когда говорите, что вероятность дождя 80%, вы абсолютно правы: в такие дни дождь идет в 80% случаев. Но когда дождь менее вероятен, вы завышаете цифры. Вы боитесь злых твитов от людей, которые оставляют свои зонты дома, а потом обвиняют вас во влажных проделках неба. Так что, когда вы прогнозируете 20% вероятность дождя, на самом деле он идет только в 10% случаев. Вы преувеличиваете вероятности, чтобы уменьшить количество недовольных писем.
Возможно, если бы люди лучше понимали вероятности, вы могли бы говорить то, что думаете на самом деле. Кажется, люди воспринимают "10%" как "не случится". Если бы они приняли его истинное значение ("случается один раз из десяти"), тогда вы могли бы раскрепостить свой язык и произнести “числа из глубин своей души”. А до тех пор вы — торговец полуправдами.
А теперь назад в студию.
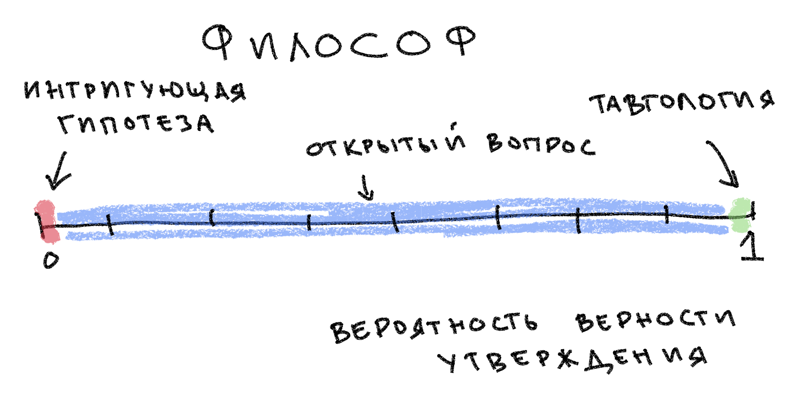
Привет! Вы - философ. Вы читаете странные книги, пишете ещё более странные и любите заходить в бар в компании священника и раввина.
Также, вероятности вас не пугают.
"Пусть вероятное останется у эмпириков", - говорите вы. Вы ищете идеи, которые кажутся нереальными. Вы задаете вопросы, на которые никто другой не решится, и думаете мысли, которые никто другой не подумает — в основном потому, что они занудные, технические и, скорее всего, неверные. Но это-то и хорошо для вас! В лучшие времена вы даете импульс новым областям знания. Психология, от Аристотеля до Уильяма Джеймса, имеет свои корни в философии. Даже в худшие времена ваши исследования провоцируют и освежают нас как ничто другое.
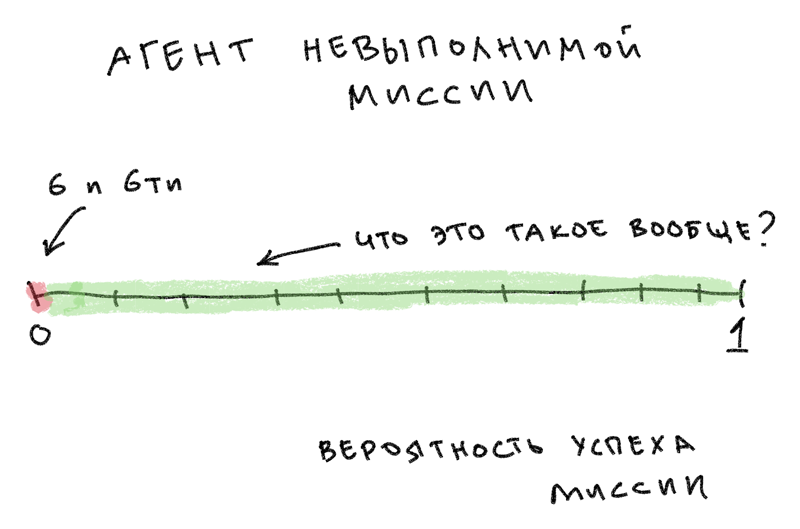
Здравствуйте! Вы агент “Невыполнимой Миссии”. Вы спускаетесь с потолков в запертые хранилища, цепляетесь присосками к небоскрёбам и раскрываете свою истинную личность предателям, с которым у вас пересеклись пути.
Кажется, вы не понимаете, что значит "невозможно".
"Невозможно" не означает "так же рутинно, как квартальный отчет о доходах". Это не значит "очень редко" или "довольно сложно" или "уф, хорошо, что лезвие ножа остановилось в миллиметре от глаза Тома Круза". Это значит "неосуществимо". И тем не менее это продолжает происходить. Название вашего фильма так же лживо, как и его захватывающая музыкальная тема.
В этом вы не одиноки. Вся художественная литература искажает вероятности. Один из моих любимых сериалов - “Огни ночной пятницы", скромное повествование о жизни маленького техасского городке, показывающее заботы и тяготы обычных людей. Но даже этот эталон правдоподобия кажды раз заканчивает повествование футбольной игрой с уникальными драматическими моментами: пасом на 90 ярдов, фамблом у линии ворот или ударом, отскакивающим от перекладины. Это заставляет меня задуматься: проецируем ли мы свои невероятные фантазии на экран телевизора, или же это телевизор внедряет фантазии в нас?

Здравствуйте! Вы - капитан "Тысячелетнего сокола". Вы - головорез, проходимец и мошенник с золотым сердцем. Ваш партнер по жизни - восьмифутовая космическая собака в бандольере.
К тому же, вы полностью отвергаете вероятности.
Вы не человек трезвого размышления и стратегического планирования. Вы - контрабандист, свергатель империи. Вы - быстрорукий дерзкий авантюрист, убивающий Гридо, для Вас сомнение - смертельно, а колебание - ещё хуже. В окопах нет места для вероятностников, а вы провели свою жизнь в окопах. Для вас, трудоёмкие вероятностные расчёты были бы так же обременительны, как и невротичный золотой робот, который постоянно твердит: «О, боже мой!» и «Если позволите мне заметить, сэр…»
Мне хочется верить, что в каждом из нас есть частичка вас. Вероятности хорошо служат нам в моменты спокойного и вдумчивого размышления, но иногда нам нужна вера, не покоящаяся на твёрдых фактах. В моменты инстинкивного действия, душа, спутанная вероятностям, может отпрянуть от необходимого прыжка. В такие моменты иногда нужно просто забыть о цифрах и лететь.






Комментарии
Оценивать вероятность проплаченного журналиста? Это пять!
Лиля Ахеджакова жужжит одинаково.
Перевод просто чудесный!)
Мне просто текст понравился, оптимистично написано, и картинки хорошие!
Если что теория вероятности это раздел математики, а не вот это вот все радостное!
Дел
Текст смешной местами, но, мягко говоря, очень сильно неверный.
Впрочем, в США 100% общественных и гуманитарных наук и 95% естественных представляют собой либо грантоедство, либо дилетантизм.
В свое время научно-популярная книга Тарасова "Вероятность.."
сильно повлияла на мировозрение и правильное понимание мира.
Там вступительная часть написана интересней и познавательней.
Случайность - это фундаментальное свойство природы (корпускулярно-волновой дуализм и квантовая механика подтверждает). Бытовое понимание вероятности, не связанное с независимыми испытаниями слишком примитивно.
То есть, вы полагаете, что вероятность не является чисто математическим приёмом... призванным исключительно с целью компенсировать наше незнание скрытых параметров?)
Какие могут быть скрытые параметры у сертифицированного ФСБ генератора шума (случайных чисел)?
Суровый вопрос подняли!
Угу. Вы бы ещё привели в качестве примера ряд, состоящий из простых чисел, расположенных по возрастающей... )
Зачем?
В качестве примера чего?
В качестве примера случайности. До сих пор не найдено закономерности в появлении простых чисел. Каждое следующее нечётное число может быть простым... с некоторой вероятностью.)
Похоже надо сближать точки зрения.
Говоря "не найдено" Вы говорите о непознанном.
Говоря о случайности, я говорю (к примеру) о напряжении на входе радиоприёмника, наводимом экваториальными грозами.
Вы знакомы с Яной Хазиной? Так вот, она утверждает, что колебания напряжения на входе радиоприёмника не являются случайными. В том смысле, что каждое колебание представляет собой цепочку из связанных друг с другом причин и следствий. И, имея достаточные вычислительные ресурсы, эти цепочки можно восстановить... )
Теперь почти понятно.
Детерменизм Ваше всё?
В классической механике да, у каждого следствия есть своя причина. В квантовой механике не так. А что касается Яны, то девчонка этого просто не понимает... )
А знаете, Яна в этом своем мнении далеко не одинока, у нее есть серьезные сторонники. Некоторые физики, среди которых даже нобелевские лауреаты наличествуют, имеют схожую точку зрения. Например, Хоофт (Gerard `t Hooft), нобелевский лауреат по физике, кучу статей и даже целую монографию написал на эту тему: см. например G. `t Hooft. The Cellular Automataon Interpretation of Quantum Mechanics, Springer, 2016 (монография open-access , между прочим). Он там прямо черным по белому с самого начала, в предисловии, оглашает вот такую крамолу:
И похоже, что он не очень-то и неправ. :)
Не споря с Вами а просто комментируя.
Нет ни одного утверждения. Одни предположения, которые сводятся к супердетерменизму, который сводится к религиозной догматике. Извините.
У кого нет ни одного утверждения? У Хоофта? А Вы что, уже всю его монографию прочитали? Там 300 страниц почти. :)
PS. А вообще математически доказано, что при вполне разумных физических предположениях случайность и жесткий детерминизм экспериментально неразличимы.
"PS. А вообще математически доказано, что при вполне разумных физических предположениях случайность и жесткий детерминизм экспериментально неразличимы."
Вот это вымораживает.
Когда надо говорить о предельном миропонимании некоторые допускают невъебен.. й компьютер, который может всё посчитать.
Когда их припрёшь к стенке, начинают говорить о том, что "1 математически доказано, что при вполне 2 разумных физических предположениях случайность и 3 жесткий детерминизм экспериментально неразличимы."
1 Кем доказано?
2 При каких предположения?
3 Кто сказал?
Например, вот эту статью прочитайте. Она в открытом доступе, журнал тоже вполне солидный.
https://www.mdpi.com/1099-4300/25/5/830
А что говорит эксперимент?)
Я выше написал --- случайность и детерминизм экспериментально неразличимы ввиду неизбежной ненулевой ошибки измерения физической величины. Это теорема.
Нет, так не годится. Рассмотрим случай разделения волновой функции фотона полупрозрачным зеркалом. Ставим на пути отклонившейся половинки детектор. Какова будет вероятность его срабатывания?
Одна вторая... И если он не сработал, значит ли это, что вероятность срабатывания второй половинки 100 процентов?)
Не в этом дело, а в том, что этот процесс имеет две модели: как чисто вероятностную, основанную на предположении об архимедовости, так и жестко детерминированную, основанную на неархимедовости.
Волновая функция может рассматриваться как непрерывная, т.е. как характеристическая функция абсолютно непрерывной случайной величины, имеющей, стало быть, плотность вероятности, а может и как дискретная, т.е. как характеристическая функция дискретной случайной величины. Обе функции живут в сепарабельных гильбертовых пространствах. И экспериментально выяснить, какая волновая функция "на самом деле" невозможно, потому что плотность вероятности в эксперименте строится как непрерывная огибающая конечного числа значений. Вот и все. Вероятность возникает и там, и там, и она одна и также в смысле значения, но происхождение ее абсолютно разное: в одном случае (непрерывном) она считается "извечно существующей" характеристикой процесса, а во втором --- обусловлена сложностью жестко детерминированного процесса. Экспериментатор может выбрать любую понравившуюся ему модель --- такая вот свобода выбора. :)
Это одно из проявлений модельно-зависимого реализма, говоря словами Хокинга (и Млодинова).
Может. Однако выбирают то, что проще и что работает. Да, ошибка измерения всегда есть (intrinsic). Но было бы нелогично для расчётов траекторий космических аппаратов использовать стохастические дифференциальные уравнения вместо Лагранжевой механики. С другой стороны для описания финансового рынка стохастические дифференциальные уравнения самое то. Хотя инсайд работает там лучше всего. Уравнения решают те, у кого нет инсайда. Лохи то есть.
Насчёт Яны, которая считает, что вероятности нет. Очевидно "вероятность" живёт в мире идей (Платоновском). Но если идеи могут изменять мир, притом мир материальный, - а они могут - то трудно отрицать их существование.
"Вероятность существует" - Воланд. А Яна - это Берлиоз(иха).
Док, вы знакомы с пролётным детектором? Это такая штука, которая не полностью перекрывает канал. Ща объясню...
Допустим, площадь сечения оптического кабеля равна 3х3 клеточки. Так вот, площадь детектора равна одной клеточке. И располагается он по центру канала. Таким образом, мы не уничтожаем эту половинку волновой функции. А позволяем ей лететь дальше. Триллион раз в секунду... включаем и выключаем мы детектор! Как вам такое?
В конце-концов, мы заставляем эту чёртову половинку провзаимодействовать с детектором! И её вторая половинка тут же коллапсирует. Да, будучи отнесённая хоть на противоположный край Вселенной!
Кароч, что остаётся в сухом остатке? Даже если исключить это устройство с пролётным детектором, мы знаем число, которое передали. И они знают число, которое передали нам... Поверьте, это не так уж и мало!)
Хоть и не мне адресовано, но отвечу аналогией.
Имеется круговая волна на воде, постоянно бежит, не затухая. Мы с вами находимся на диаметрально противоположных концах от центра волнообразования, но я нахожусь на полпериода волны ближе к центру, чем Вы. А мерить мы с вами можем только горбы или впадины: горб - это 1, 0 -- впадина. Поэтому когда Вы измеряете 1, у меня 0, и наоборот. И НИКАКОЙ информации ни от меня к Вам, ни от Вас ко мне НЕ ПЕРЕДАЕТСЯ, хоть какое расстояние между нами ни будь.
Ну и формально: нет никаких "половинок" у волновой функции. Есть волновая функция --- это характеристическая функция распределения случайной величины. Есть ДВЕ случайных величины, каждая со своим распределением, есть их характеристические функции. А вот СОВМЕСТНОГО распределения этих ДВУХ случайных величин может и НЕ БЫТЬ: это упрямый математический факт. А нет совместного распределения --- НЕТ И ОБЩЕЙ ВОЛНОВОЙ ФУНКЦИИ. Физикам почему-то не всегда это заходит: они считают, что совместное распределение у двух случайных величин есть всегда. А это не так.
Почему не заходит? Как раз с этим-то всё в порядке. А так всё верно. Я про половинки уже устал объяснять. А так же о том, что фотоны спутанными быть не могут (нет соответствующих законов сохранения). Они почтальоны, перенесчики информации. Более того, с волновой функцией фотона большие проблемы. Так как фотоны рождаются и умирают, то закон сохранения для плотности вероятности фотона невозможно обеспечить. Это раз. А два - это то, что Δx, там где локализован волновой пакет фотона, слишком большой (Δx≫λ≫Δλ).
Вот! С этим и я согласен. Хоть и я не физик, но математически это все корректно выглядит.
Атом излучает фотон в течении 10-10 секунды. За это время электрон на внешней орбитали успевает сделать 100 000 оборотов вокруг ядра. Это соответствует частоте видимого света. И всё это время электрон возбуждает в окружающем его электромагнитном поле волну... сферическую волну, в первом приближении. (Почему сферическую? - спрашивайте, отвечу.)
Один оборот электрона вокруг ядра соответствует одному периоду волны. Наглядной аналогией будет круговая волна на поверхности воды от брошенного камня. Ещё лучше будет, если мы возьмём... да, листок в клеточку.
Итак, рисуем 100 000 концентрических окружностей. И заставляем их... расширяться, силой мысли, разумеется. Нарисовали?
- Т-танки идут р-ромбом, ф-фотоны идут ц-цугом!
Вещал нам поэт Роберт Рождественский... (Василий Аксёнов. Таинственная страсть. Читали? - прим. моё) И как в воду смотрел! Именно такими словами описывают поведение фотонов многие наблюдатели. Цугом, значит, друг за другом. И как бы намекая, что невозможно определить, где кончается один фотон, и начинается следующий. Впрочем, не будем отвлекаться...
Проведём вертикальную и горизонтальную прямые из центра окружностей. И ещё одну - под углом в 45 градусов. Да, это оно, полупрозрачное зеркалó. Извините, что в рифму...
Итак, фотонная волна падает на полупрозрачное зеркало... и взаимодействует с атомом серебра. Тот возбуждается и... начинается фотоноизвержение. Под углом в 90 градусов к пришедшему лучу света. А где же сфера, возможно, спросите вы?
Сфера образуется у одиночного атома, вдали от других атомов. В нашем же случае у нас имеется поверхность зеркала, которая является простейшим оптическим устройством. Да, это она, вычитающая интерференция. И соседние атомы серебра вносят в неё свой посильный вклад.
Итак, одна половина... волновой функции фотона отразилась под углом в 90 градусов, а другая прошла прямо, сквозь зеркало...
Можем провести ещё две парочки прямых... так, чтобы образовались сектора... сектора обстрела, как говорим мы, артиллеристы... ну или волновой пакет, как говорят физики. И даже невооружённым глазом будет заметно, что пакет расплывается... по мере расширения окружностей. Ну, это так, в качестве дополнения. Вообще говоря, этот рисунок даёт богатую пищу для размышлений.
Главное, не ограничивайте свою фантазию!)
Очень образно. :)
Только вот половина волновой функции напрягает как-то. Да и вообще, хоть даже и целая функция. Как это "она отразилась", да еще и от зеркала? Если волновая функция --- это функция (а она таки да), то у нее должна быть область определения и область значений. Ну, меня так в школе учили. И где же они в этом красивом описании? Нету. А значит, и функции нету, даже и половинки. :)
А фотоны да, есть. И волны есть. :)
Танки идут ромбом,
Фотоны летят цугом.
Кто этот мир придумал,
Наверняка, был Богом!
" - S’il y a quelque chose de fondamental dans ce monde, c’est bien l’amplitude du photon, égale à 1."
Силь йа келькью шюз... тьфу, ты... то ись, в переводе с немецкого, если и есть в этом мире что-то фундаментальное, так это амплитуда фотона, равная 1. Если вы читали мои работы и слушали мои выступления на симпозиумах и конференциях, то вам должна быть знакома эта фраза, которую я не устаю повторять вот уже на протяжении... эмм... многих лет, да!
Что вас смущает, половинки волновой функции фотона? Но это зависит только от прозрачности зеркала. Если мы сделаем зеркало менее или более прозрачным, тогда волновая функция может разделиться в соотношении, например, 1/4 и 3/4. Почему нет?
Приглядимся повнимательнее к круговой волне на воде. У вас не возникает никаких мыслей по этому поводу? А между тем, и круговая волна на воде, и электромагнитная волна в нашем 3-мерном пространстве являются поперечными волнами... Правда, в первом случае волна колеблется в дополнительном измерении, то есть, в третьем... Нет, нет, я не хочу сказать, что и для электромагнитной волны тоже необходимо ввести ещё одно, дополнительное, четвёртое измерение. Боже упаси!
Как воспримут волну на поверхности воды жители двухмерного мира? Как чередование сжатия и растяжения. Что будет аналогом ему в нашем мире? Продольные волны... да, а не электромагнитные. Отнюдь! Впрочем...
Впрочем, идея о наличии в нашем мире четвёртого и пятого измерений представляется мне весьма плодотворной. И я бы не стал её отвергать, вот прямо так, с порога.)
Меня смущает сам термин "половинка волновой функции". Например, вот волновая функция свободной частицы: 𝚿(x,t)=Aei(kx-ωt) Что есть "половинка" именно ЭТОЙ волновой функции? Напишите, пожалуйста, эту "половинку" в явном виде для ЭТОЙ волновой функции, заданной в явном виде.
Кажется, мне удалось найти удачную и наглядную аналогию... Заменим наше 3-мерное пространство 2-мерной поверхностью. Тогда вместо фотонной сферы будет расширяющаяся окружность, а колебания поля будут происходить в плоскости поверхности и перпендикулярно движению волны. И это будет доступно нашим органам чувств и измерительным приборам... Колебания же перпендикулярно поверхности будут происходить в дополнительном измерении, которое мы можем воспринимать только в виде проекции на нашу поверхность... Так вот, эта круговая расширяющаяся волна, колеблющаяся в дополнительном измерении и будет фотоном. С амплитудой, равной 1. То есть, колебаться будут все детекторы, через которые она пройдёт. Но, в дополнительном измерении, недоступном для нас... А срабатывать будет только один из них. После чего вдоль окружности пойдёт сигнал на схлопывание. Мгновенное схлопывание. И там нету ограничения на скорость... Что же касается формулы волновой функции, то она зависит от оптической системы и от размера части волновой функции.)
Ну, то, что есть (или чего нет) в измерениях, недоступных для нас, можно и нужно считать несуществующим. Потому что если это "что-то" в принципе никак не воздействует на то, что мы можем физически померить, то этого "что-то" просто нет, поскольку никакой информации об этом "что-то" получить в принципе невозможно. Это "что-то" даже в модель включить будет тяжело, раз оно себя вообще никак не проявляет. Я попытаюсь объяснить, что именно мне не нравится в этой Вашей аналогии, с помощью другой Вашей аналогии, которая мне нравится и которая рабочая.
Ваша реально работающая аналогия --- это лист бумаги в клеточку. Берем Ваш любимый лист бумаги в клеточку и рисуем на нем прямую. Лист бумаги --- это действительная плоскость. Клеточки --- решетка на действительной плоскости. Факторизуем плоскость по решетке и получаем --- внимание!!! --- тор! Трехмерный объект! Появилось ЕЩЕ ОДНО измерение, о как! Вы хотели еще одного измерения? Так вот оно!
А что стало с прямой на плоскости? А она превратилась --- внимание!!! --- в обмотку тора! Причем эта обмотка всюду плотная на торе, если угловой коэффициент прямой иррационален, и периодическая (=замкнутая), если рационален. Записывая уравнение обмотки тора в цилиндрических координатах и заменяя всякие синусы-косинусы комплексным представлением, получаем --- ну что бы Вы думали? --- волновую функцию свободной частицы, причем как раз в той форме, которую я написал выше в своем комментарии. Вот теперь можно задаваться вопросом, а как интерпретировать клеточки, а что будет, если нарисовать много прямых, а не одну, или взять не плоскость, а трехмерное пространство, и т.д, И на все эти вопросы можно получить вполне конкретные, математически корректные ответы, имеющие, к тому же, вполне ясный физический смысл. Откуда берутся всякие базисы, которые выбирает экспериментатор? А с какой стороны он на тор с обмоткой смотрит, значит, такой базис он и выбрал для записи этой обмотки! Может с другой посмотреть, другой базис будет. И интерференционную картинку можно получить, аккурат как в двухщелевом эксперименте. Так даже соотношение неопределенности можно вывести, в энтропийной форме, причем, фактически, из школьной формулы sin2x+cos2x=1. Ну, немножко подкрутить ее, и все получится. :)
Но что вот тут Вы имеете в виду?
Что такое "часть волновой функции"? Отрезок прямой на бумаге в клеточку? НО можно МАТЕМАТИЧЕСКИ ДОКАЗАТЬ, что если есть в мире хоть какая-то причинность, то если на бумаге в клеточку нарисовать отрезок прямой, пусть самый коротенький, то на торе появится ВСЯ обмотка, т.е. вся волновая функция! Нет у нее кусков, половинок, четвертинок и т.д. По одному самому маленькому кусочку АВТОМАТИЧЕСКИ воспроизведется все! Такая вот голограмма, ага.
И никаких "неведомых не обнаруживаемых сущностей". :)
И это вы ещё не упомянули следующую логическую ошибку. Ведь, если фотон отражается от атома серебра в полупрозрачном зеркале, то, разве, остальная часть волновой функции не должна схлопнуться?
Ведь, что такое отражение как не взаимодействие? Атом сначала должен поглотить один фотон, а потом излучить другой. Однако, Роджер Пенроуз в своём "Новом уме короля" словно не замечает этого и с упорством, достойным лучшего применения, продолжает пихать этот пример из издание в издание.
Док, положа руку на сердце, скажите нам, что вы думает об этом?)
Я НЕ ПОНИМАЮ, что такое "часть волновой функции"!!! Ну вот совсем не понимаю.
Какой "другой фотон"? Вы умеете различать такие фотоны? Как Вы это делаете? Мы же не можем нанести метки на фотоны как на подопытных мышей или мух.
Есть квантовая система (в данном примере, атом серебра), есть воздействие на эту систему (поглощение фотона атомом), есть реакция системы (испускание фотона атомом). Больше ничего нет. Есть МНОГО таких систем, набираем статистику, прогнозируем поведение на основе мат. модели. Проводим эксперименты, сверяем результаты с предсказаниями модели, если совпадают, то все, модель годная. Больше ничего сказать нельзя.
Вообще, где находится фотон, когда он перепрыгивает с орбитали на орбиталь? И сколько времени длится этот "перепрыг"? Эти два вопроса лишены физического смысла (по крайней мере, ПОКА лишены физического смысла), т.к. на первый надо отвечать "нигде", потому что на второй вопрос ответ "за время, равное нулю". "Схлопывание" волновой функции --- это НЕ физический процесс потому что физический процесс происходит за ненулевое время, а волновая функция, согласно современным представлениям, схлопывается "мгновенно". Значит, волновая функция --- это просто наша модель, удобный математический объект, позволяющий вычислять вероятности перехода физической системы из одного состояния в другое. Даже сам термин "состояние", строго говоря, не имеет физического смысла, но он удобен потому что позволяет объяснить. почему одинаковые системы ведут себя по-разному при одних и тех же воздействиях на них и, главное, сосчитать соответствующие вероятности той или иной реакции системы на одно и то же воздействие. Ведь это чисто автоматная терминология, из математической теории, а именно, из теории автоматов!
Ну, а коль скоро это так, раз волновая функция --- это функция в математическом смысле этого слова, то нет у нее никаких "частей", "половинок" и т.п. Или надо вводить ФОРМАЛЬНОЕ математическое определения этих понятий, раз уж волновая функция сама по себе математический объект, а именно, характеристическая функция распределения.
Как говорил мой учитель физики, аналогии легко могут завести не туда: например, "ананас" пишется слитно, но "а на вас" --- раздельно. :)
С частями всё как раз понятно. Если вы вводите предельную, максимально возможную скорость взаимодействия в системе, как у старика Эйнштейна... то всё остальное вытекает логически и автоматически.
Плоская волна света, интенсивностью один фотон в секунду, падает на группу детекторов, но срабатывать будет всегда один и только один, выбранный случайным образом. Отсюда делаем вывод, что детектор может сработать от любой, самой маленькой части... волновой функции. Да, чёрт возьми, ВОЛ-НО-ВОЙ ФУНК-ЦИ-И!
Ладно, не обращайте внимание. Обзовите это как хотите. Да хоть сферой квантового потенциала... )
Кем выбранный? Имеем физический факт: срабатывает ровно один детектор. Случайный. НО если много фотонов послать, то получим распределение. Почему всегда только один? Фиг его знает, жизнь так устроена: Волга впадает в Каспийское море, а детектор срабатывает один. А нам надо всего лишь предсказать, с какой вероятностью фотон попадет туда или сюда, или с какой вероятностью Волга впадет ЗАВТРА в Каспийское море. Во втором случае с вероятностью 1 (а через 100 млн лет --- фиг знает), а для фотона --- надо считать, используя волновую функцию и правило Борна. Все, это работает. Пока работает.
Но вывод Ваш не обоснован --- из того, что Вы написали, можно только сделать вывод, что детектор срабатывает от попадания на него фотона (как Каспийское море пополнится водами Волги), а произойдет это попадание с такой-то вероятностью. Больше ничего. И никаких частей волновой функции.
Сфера квантового потенциала --- тоже математический трюк, по сути-то. Удобный для тех, кто любит и умеет пользоваться этим инструментом. Некоторые мои коллеги вполне уверенно и эффективно его используют. Заметим, я сейчас не об интерпретации КМ говорю, а просто о мат. модели. Работает? Ну и хорошо, хотите с помощью нее рассчитывайте, хотите с помощью другой модели. Какая больше нравится. Лишь бы результат правильный давала, в смысле, правильно предсказывала исход экспериментов.
Модельно-зависимый реализм в чистом виде.
Ладно. Изменим чуть-чуть рассуждения старика Роджера. Перекрывать будем не отражённый канал, а прямой, через зеркало. Окей. Ничего не изменилось. По-прежнему продолжают интерферировать...
Итак, какой же вывод? Фотон провзаимодействовал с атомом серебра и "отразился" под углом в 90 градусов... В кавычках, док, в кавычках... И что же произошло с той частью его волновой функции, что прошла сквозь зеркало? Она не сколлапсировала!)
Что такое "часть волновой функции"? Куда она прошла? Волновая функция --- это характеристическая функция распределения. Идеальный объект из мира идей. А зеркало --- объект реального мира.
Например, погрузили кольцо в воду, наполовину. Целое кольцо выглядит теперь согнутым посередине, да и видимый размер кольца вроде как изменился... Это как трактовать? Что число 𝞹, погрузившись в воду, превратилось в 𝞹/2 что ли? Поймите, для меня это звучит точно так же, как и "часть волновой функции, прошедшая сквозь зеркало".
Хочите, чтобы я заменил волновую функцию на просто волну? Да ради бога!
Итак, волна разделилась на две части... Так лучше звучит?)
Хуже. Для того, чтобы сосчитать вероятность, нужна корректная мат. модель, причем прошедшая экспериментальную апробацию. Иначе доверие к результату нулевое. Волновая функция + уравнение Шредингера --- это (пока) именно такая корректная мат. модель. И в ней никаких "половинок" от волновой функции нет.
Шредингер ведь зачем-то заменил волновое уравнение на свое? Чего бы ему не пользоваться просто волновым уравнением? Ан нет ...
Хорошо. Вот мы и подошли к теме двухщелевого эксперимента. Теме, которой посвящено целое море литературы... Волна фотона разделяется там на две части, которые начинают интерферировать друг с другом. Или вы предпочли бы по-другому сформулировать?)
Да, по-другому: это не разделение волновой функции пополам, и даже не разделение волны пополам, это принцип Гюйгенса-Френеля.
Надо будет попросить доктора Спинора... или, как говорят у них в Оксфорде, доктора Спайнера, написать статью об этом. У него хорошо получается. Кстати, вы в курсе, что Спинор коренной англичанин?)
Да кокни он, кокни! Шотландский кокни из Уэльса. :)
Между прочим, Спинор самостоятельно выучил русский язык. Причём, сделал это ещё в глубоком детстве. Не без помощи родителей, конечно. Но, тем не менее...
Дело в том, что русский математик и русский физик это своеобразный бренд. Примерно такой же, как бразильский футболист, английский гитарист или русский шахматист. И действительно, многие иностранные шахматисты не только знают русский, но и берут себе русские имена, под которыми играют в он-лайн турнирах.
Ну и в самом деле, жизнь на захолустном острове на самом краю Европы была далеко не сахар. Постоянные дожди вперемежку с тяжёлыми лондонскими туманами сделают меланхоликом кого угодно. Повсеместный бытовой алкоголизм и деревянные игрушки, приколоченный к полу... Какое будущее было уготовано юному Спинору?
Дикие нравы местных аборигенов, орущих на заполненных под завязку футбольных стадионах, где 22 таких же придурка гоняют один(!) кожаный мяч на всех... И только лишь виртуозная игра на электрогитарах и барабанах хоть как-то оправдывала существование этого острова. И такие вокально-инструментальные ансамбли, как Битлз, Пинк Флойд, Лед Зеппелин, Назарет, Блэк Саббат, Дип Пёрпл и ряд других не дадут соврать...
Поговаривают, что во времена Юлия Цезаря на этот остров ссылали опальных военноначальников и философов... )
Страницы