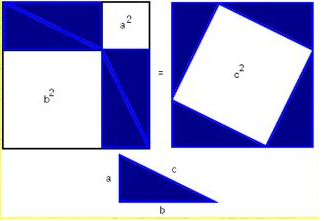
Вероятно, почти все помнят школьное доказательство теоремы Пифагора (ТП).
В книге Нила Стивенсона "Анафем" чертеж необычного доказательства "теоремы Адрахонеса" (аналог ТП в мире автора) играет существенную роль в сюжете.
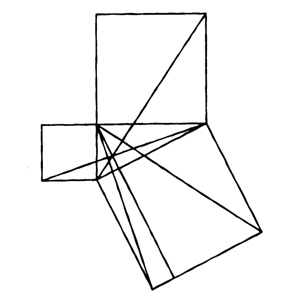
Доказательство для тех, кто не сообразил сам
Это доказательство натолкнуло меня на доказательство с совсем простым чертежом.
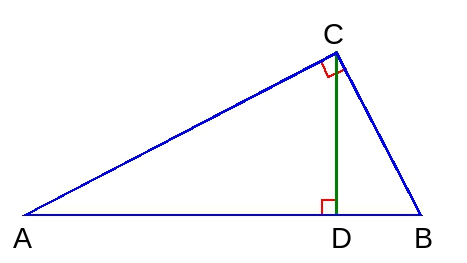
Доказательство
Использованные источники:





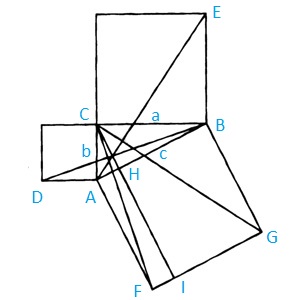
Комментарии
Браво!
Откуда вы взяли подобие треугольников?
Прямоугольные треугольники с одинаковыми углами.
Понятие "прямоугольный треугольник" уже включает угол.
Вы в своеи "доказательстве" использовали теорему Пифагора, собственно, то, что и хотели доказать.
Врочем от вас ничего другого и не ждешь.
Ты зря быкуешь, быдлячок... Впрочем, от тебя с твоей кармой 2% вряд ли стоит ожидать большего.
Признак подобия "по двум углам". Опровергни, если сможешь...
Вы два сапога пара ))))))
Еще раз, повторю, может так получится понять у вас, двух мегамозгов.
Итак он доказывает теорему Пифагора, используя, ба бам!, теорему Пифагора.
Поэтому его доказательство такое короткое. Он говорит поскольку теорема Пифагора верна, то из этого следует, что теорема Пифагора верна.
Если вы этого не видите, инженер, то у меня для вас плохие новости.
Ты спросил о подобии треугольников?
Тебе ответили, что подобие по острому углу прямоугольного треугольника? Что не так, умник? Не нравится "по острому углу...", пусть будет "по двум углам: острому и прямому'. Это одно и тоже...
Ну давай, расскажи мне, как вводится определение прямоугольного треугольника? И как признаки подобия жесточайше увязаны с теоремой Пифагора?
Вы безнадежны. Не стоит на весь ресурс показывать свою тупость. Я уже вам даже намек дал, что бы исправиться, но вы слишком недалеки.
Итак. Подобие треугольников , получающихся если из прямого угла опустить высоту на гипотенузу нужно доказывать, а не просто сказать , что они подобны. Такое происходит только у прямоугольных треугольников. На этом подобии и стоится "доказательство". А доказывается это подобие в том числе через теорему Пифагора.
Поэтому Владимир просто написал что теорема Пифагора верна, потому что теорема Пифагора верна. Он глуп , что бы осознать это. Вы получается тоже.
Послушай, олень... Объясняю последний раз: признак подобия по двум углам. Если треугольник прямоугольный, то можно говорить о признаке подобия по острому углу, по умолчанию понимая, что второй угол - прямой.
Общий острый угол делает доказательство подобия в данном случае очевидным.
Понятие подобия в общем случае не привязано к Пифагору.
Ну вот и оскорбления пошли. У людей с низким интеллектом всегда так. Поздравляю вас.
Итак, мой недалекий друг, вы в этой части обошли Пифагора, что разумеется можно сделать, так так сама теорема конечно верна. Но вам тогда нужно доказать правомерность сокращения К. Дерзайте.
Для удобства сконцентрирую вам мысль. Ваше доказательство подобия происходит попарно. К1, к2 к3 , далее же Володимир в уме приравнивает их, выносит за скобки и сокращает как общий множитель. Докажите что к1 равно к2 равно к3 равно к.
Это ты, что ли, переживаешь об обзываниях? Нашлась девственница из публичного дома.
Насчёт k автор ошибся.
https://aftershock.news/?q=comment/14012892#comment-14012892
Ааа ааа , Аааааааа, ааааааааа.
Вот это эпичный слив. На моей памяти такое наверно еще не случалось.
Значит Владимир обкакался и вы вместе с ним тоже обкакались ?
Как интересно жить.
Надеюсь вы признаете, что вы эээээ обгадились и принесете извинения.
Твоё?
Твоё?
Олень, успокойся... Ты ни черта не смыслишь ни в признаках подобия, ни в теореме Пифагора. Иди в школу, эксперт.
Процитируйте мое ошибочное утверждение.
Обращаю внимание, что бывают неверные утверждения, а бывают пробелы в обосновании. Уточните, что именно Вы называете "ошибкой": неверное утверждение или пробел в обосновании?
Давайте я.
Ваше к не может быть единым и сокращаться. Так как малый треугольник не может относится к большому и к среднему (даже вам должно быть очевидно, что они разные) с одинаковым коэффициентом К. Они действительно пропорциональны, но через три разных коэффициента к1, к2, к3, и эти коэффициенты совершенно точно не равны (вернее могут быть равны два из них в частных случаях, но не могут быть равны все три). И значит сокращать их нельзя и значит ВСЕ ваше доказательство неверно.
Вы обосрались.
То, что ты дебил, уже стало ясно. Обсуждать с тобой что-то смысла нет. Так что, иди лесом. Бан на неделю.
Ошибочное, потому что не довели до конца.
Система уравнений:
Первые три уравнения: отношения площадей треугольников, как квадраты соответствующих линейных размеров:
S1/S2 = a1^2 / а2^2
Кроме того: сумма S двух малых треугольников = S большого треугольника.
Кроме того: c = c1 +c2, где с - гипотенуза, а с1 и с2 - её части, полученные при пересечении с высотой.
Вот из этой системы вы путем алгебраических преобразований получите искомое с^2 = а^2 + b^2.
Только такие кульбиты ничуть не проще и не лучше, чем обычные школьные доказательства. Хотя имеют право на существование. И через подобие треугольников теорему Пифагора доказывали:
Вы ввели коэффициент пропорциональности k. Во-первых, он лишний (только усложняет). Во-вторых, никто не обещал (а вы не доказали), что коэффициент пропорциональности при сравнении разных треугольников и их линейных размеров - одинаковые. Вам уже несколько раз об этом разные люди сказали.
Еще раз: ПРОЦИТИРУЙТЕ тот МОЙ фрагмент который критикуете. Иначе у Вас беседа с самим собой получается.
Почему k - одинаковое?
(Это надо доказать).
Я использую теорему
a, b и c - аналогичные линейные элементы в подобных треугольниках (гипотенузы).
Площади этих треугольников пропорциональны квадратам длин этих элементов (характеризующих линейный размер). k - коэффициент пропорциональности между площадью и квадратом линейного размера (гипотенузы). Существование такого коэффициента вытекает из вышеприведенной теоремы.
Принял. Да, вы правы.
Сначало желательно было написать S1 / S2 = a1^2 /а2^2, откуда S1 = k1*a1^2 и S2 = k2*a2^2. Получаем k1=k2 для выполнения равенства в соотношении.
Однако остаюсь при своем мнении. Есть один нюанс:
Прежде, чем изучать различные типы "движения" и "признаки подобия", для лучшего понимания желательно ознакомиться со всеми свойствами углов и треугольников. В т.ч. тригонометрией, а значит, прямоугольными треугоььниками и т.д. Методологически, в школе так и изучают: движения и подобия много позже, чем понятие прямоугольного треугольника (значит, и теоремы Пифагора).
Вы для доказательства теоремы Пифагора взяли "математический аппарат будущего изучения". Это не запрещено, но методологически не совсем верно... Скажем так, первое доказательство теоремы Пифагора для школьника должно быть как можно более простым и наглядным. И доказательство с помощью четырех прямоугольных треугольников, по разному уложенных в квадрате - самое простое и наглядное (по личному мнению).
P.S.: Вы знаете, что sin, cos, tg, ctg и др. тригонометрические функции - это "ошибка истории"? Их вообще бы можно было не вводить, если сразу пользоваться теорией функций комплексного переменного:
Но sin, cos, tg, ctg и др. продолжают изучать в школе. Так как до ТФКП многие дорастают мозгами лишь в ВУЗе.
А так-то, да... Скинуть тригонометрию с парохода современности путём элементарных выводов из ТФКП... Красота!
Оригинальный у Вас заход. Как по мне: тригонометрические функции - штука сложная, нетривиальная и абстрактная. Я же демонстрирую детишкам "закон площадей" на примере квадратиков: "Вот один квадратик, а вот - в два раза больше. Давай посчитаем, как увеличилась его площадь?". А потом обобщаю по принципу из анекдота "Вот так и птички" на другие формы.
P.S.: Если чо, то тригонометрия - не про прямоугольные треугольники (это только способ определения функций), а про свойства треугольников вообще: тригоно-метрия. И играть эти синусы и косинусы начинают только при "овеществлении" признаков равенства треугольников, т.е. "как по трем элементам треугольника найти остальные".
Хотите сказать, что решать треугольники ну никак не возможно без знания комплексных чисел?
Напомню, что понятие мнимого числа появилось при попытке вывода формулы корней кубического уравнения. И где тут треугольники?
Да, позже появилась геометрическая интерпретация комплексного числа, а оттуда и тригонометрические функции. Но брать это за основу тригонометрии (как по мне) - ставить телегу впереди лошади.
Если кто-то говорит о прямоугольном треугольнике, это еще не значит, что он использует теорему Пифагора. У прямоугольных треугольников есть и другие интересные свойства, например, что сумма двух острых углов равна 90о. Или что высота делит гипотенузу на части, произведение которых равно квадрату этой высоты.
Короче подучите геометрию, интересная наука.
На чертеже нет ни одной пары подобных треугольников.
Вы можете назвать две пары равных углов в треугольниках, которые считаете подобными?
Edit: а не все верно. Доказательство верное
Вы будете удивлены, но на чертеже три подобных треугольника.
Да, уже успел удивиться. Пришлось опереться на свойство Евклидовой геометрии: все треугольники имеют сумму углов равную сумме двух прямых углов.
В школе обычно подобие изучают после теоремы Пифагора. Поэтому здешнее доказательство не очень распространенное в учебниках геометрии.
Да, методологически, всё же, лучше теорему Пифагора учить до изучения механизмов подобия. Так в современной школе принято.
Но и обратное не запрещено. Более того, весьма распространено было раньше.
Бред сивой кобылы. Или двоечника. Давайте еще заявим, что все прямоугольные треугольники подобны? А?
Вы придуриваетесь, или, правда дурак?
Разумеется ∠CAD = ∠BCD, a ∠ACD = ∠CBD - подобие по двум (трем) углам.
Либо Вы круглый дурак и невежда, либо Вы настолько меня не любите, что это начисто отшибает Вашу природную сообразительность.
Да дурак он просто. Во всём.
По двум углам. ( один из них прямой) Канонично.
площадь нельзя описать при помощи циркуля и линейки. это сложное понятие и не уверен что ее можно описать без теоремы пифагора
При чем тут циркуль и линейка? Площадь прямоугольника доказывается естественно без теоремы Пифагора.
А площадь прямоугольного треугольника - это половина площади прямоугольника, ввиду того что он получается путем разделения прямоугольника на две одинаковые части диагональю.
А S это что?
Площадь.
Первый раз вижу, чтобы площадь прямоугольника выражали через квадрат диагонали. Как это работает?
Обычно вопрос начинают с цитаты. Мол, Вы написали "то-то", а я не понимаю "это".
"Тогда S(CBD) = k*a2, S(ACD) = k*b2, S(ABC) = k*c2, причем k != 0"
Где a,b,c гипотенузы этих же треугольников, а k непонятно что, но при его заданном значении площади всех треугольников на картинке должны быть равными нулю, что противоречит как самой картинке, так и свойствам материального мира. ))
Посмотрел, что вы имели ввиду, там соотношение, но из вашей записи это если и очевидно, то далеко не всем.
Ну, я то не для первоклассников писал. Очевидные вещи пропускал.
a, b, c - сходные линейные элементы подобных треугольников (гипотенузы). Я использовал факт, что площади подобных фигур пропорциональны квадратам линейных размеров. А k - коэффициент пропорциональности.
Ну в геометрию я очень хорошо умел, правда лет так сорок-сорокпять назад и не все очевидности всплывают в памяи. ))
Всё остальное ок.
Да, спасибо! Кстати, второе из приведенных мной доказательств там тоже было
Кароч, ждём Арбалета. Как он скажет, так тому и быть.)
Еще мне не хватало в этом возиться. Тут на АШ то на 0 делят, то про ТО с КМ всякие глупости пишут, а я разбирайся? Нафиг мне оно надо?
Рукопожимаю.
Низвергатели физики куда-то подевались... Я жду, когда они запилят свой космолёт на альтернативных принципах... Ну или хотя бы Ковчег. И брутально свалят недалеко, но громко.
Слова не мальчика, но мужа
Это доказательство есть в википедии, в чуть измененном виде (не через формулу площади, а через соотношение площадей)
https://ru.wikipedia.org/wiki/Теорема_Пифагора#Через_площади_подобных_треугольников
Страницы