До шестнадцатого века люди производили вычисления «столбиками». Но с развитием наук, связанных с большими расстояниями, в частности, астрономии, умножать и делить большие числа таким способом стало трудным делом – столбики просто перестали умещаться на листе бумаги. Тогда учёные пришли к решению – они степенную функцию «вывернули наизнанку» и, создав таким образом логарифм, заменили умножение и деление на более простые сложение и вычитание. В результате применения логарифмов и их свойствам экспоненциальности сложные расчёты облегчились и их результаты в графическом виде стали более компактными.
Напомним для тех, кто забыл логарифмы. Например, нам надо возвести в квадрат число 25. Можно умножить столбиком 25 на 25 и получить результат 625. Но можно в таблице логарифмов найти логарифм числа 25 и, увеличив его путём сложения в два раза, опять заглянуть в таблицу логарифмов. Там найдём искомый результат – число 625. В этом примере взяты небольшие числа, которые можно перемножить и столбиком, а что делать, если необходимо, например, возводить в степень многозначные числа или перемножать их и делить? Коротко говоря, появление логарифмов сыграло большую роль в развитии наук. Образно логарифмирование можно сравнить с микроскопом и телескопом, оно подобно им раздвинуло границы познаваемого мира. Именно благодаря логарифмированию возникла термодинамика, которая, начав своё шествие с паровых двигателей, распространилась на химию, атомную и ядерную физику, астрофизику, метеорологию и другие сферы.
Сейчас на очереди проникновение термодинамики в социалогию и экономику. И здесь возникает некоторая проблема, заключающаяся в том, что необходимо учесть специфику социально-экономических систем. Во-первых, здесь элементами систем являются не частицы, а люди с присущими им степенями свободы. Во-вторых, число людей, как элементов системы, несравненно меньше. Для сведения: в газе (воздухе) в одном кубическом сантиметре находится 1019(миллиард раз по десять миллиардов) молекул, то есть в миллиард раз больше населения Земли.
В экономических системах число их участников может быть как большим, так и совсем маленьким, начиная с одного человека (самозанятого). Поэтому надо разобраться, насколько пригодны к социологии общепринятые сейчас логарифмические ряды, успешно работающие с физическими системами.
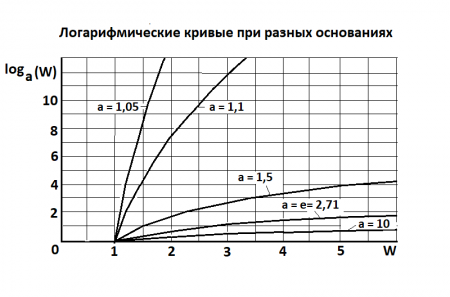
На приведённом выше графике показаны логарифмические кривые, рассчитанные по формуле:
s = loga w , (1) где: s – логарифм, a – основание логарифма,
W – логарифмируемое число
Исторически первой и применяемой до настоящего времени таблицей логарифмов я вляется «десятичная», созданная на основании a=10. Четыре века назад учёные сочли такое основание логарифмов оптимальным.
Однако позже была создана другая таблица логарифмов, названных «натуральными». К этому был причастен учёный Л.Эйлер, который ввёл в своё время в дифференциальное и интегральное исчисление странное число e=2,7182818284. Д.Бернулли исследовал это число с точки зрения «сложного банковского процента», позволяющего получать дополнительный доход, но не более чем в e раз. Эта логарифмическая система с основанием e прочно вошла в математику, но, кажется, нематематикам безразлично какую таблицу логарифмов использовать для ведения своих расчётов.
Описанные логарифмические ряды с основаниями a=10 и e = 2,718 по всей вероятности могут быть применены и в экономике.
В IXX веке Л.Больцман сформулировал понятие энтропии, опираясь именно на натуральную логарифмическую систему счёта с основанием e. Возникает мысль, не потому ли это произошло, что этот вариант логарифмического изменения численного ряда действительно ближе к природе? Но, как видно из приведённого на рисунке выше семейства логарифмических кривых «натуральный» вариант не является крайним, предельным, явно отличным от других.
Преобразуем выражение (1) в формулу энтропии по Больцману:
S0 = K. lnW0 , (2) где: K – постоянная Больцмана,
W0 – термодинамическая вероятность.
Представляется, что большая часть смысловой нагрузки в этой короткой формуле приходится на натуральный логарифм. Задаём тот же вопрос: возможно такое, что натуральный логарифм больше других подобен процессам, протекающим в неживых термодинамических системах, для которых и была создана теория Больцмана?
Если это так, то не стоит ли поискать другую логарифмическую зависимость для описания процессов в социально-экономической сфере? Например, одну из показанных на графике, когда: а = 1,5; 1,1 или 1,05?
Видимо, ответ на этот вопрос можно будет получить только при проведении практических исследований.
Что касается постоянной Больцмана, в экономическом варианте она должна быть другой, ведь люди не атомы.





Комментарии
Ага. Атомам нафиг не нужен внешний источник, чтобы не загнуться, и понятия удовлетворённости или неудовлетворённости нет. Поэтому у атомов постоянная Б., а у людей переменная.
На атомно-молекулярном уровне тоже большая неразбериха, но на человеческом гораздо больше.
Беспорядочные ковалентные связи?
В конце-концов найдётся специалист одновременно химик и социолог-экономист, найдёт аналогии, свяжет валентности с человеческими страстями и законами. Типа Бернулли, котрый вроде бы разбрасывался, но сделал многое в разных сегодняшних отдельных науках.
Я к большим специалистам себя не отношу, поэтому ограничиваюсь доступными мне скромными пределами по высоте и ширине.
Накаркаете чесслово. Подмены ХХ и ХУ на стопицот "гендеров" недостаточно что ль?
Кто сможет записать число 10 с показателем степени, состоящим из единицы и 10 миллиардов нулей?
Тот получит сладкую конфету.)
X (тыщелион) = 10 с показателем степени, состоящим из единицы и 10 миллиардов нулей
Жду конфету.
Только после того, как напишете. И если вы начнёте писать нули прямо сейчас, то... эмм... к утру закончите?)
Дык я написал Х это ваше число, условия написать в арабской нотации не было.
Окей же ж. Тогда уточняем условия. Написать это число прямо здесь, в комментарии, пользуясь ашевским текстовым редактором. В арабской нотации, разумеется!)
101010 000 000 000
Неплохо. Получилась степенная башня. Высотой в 3 этажа. А 4-этажную слабо изобразить?)
Легко
10101010
Причем работаю именно в АШ-вском "простом текстовом редакторе":
<p>10<sup>10<sup>10 <sup> 10 </sup> </sup></sup></p>
Ух ты, круто! Ну лан, окей. А можете оценить, что это за число и с чем его можно сравнить?)
Тут даже жалкому гуголу 10100 физического смысла не смогли найти:
Гугол больше, чем количество атомов в известной нам части Вселенной, которых, по разным оценкам, насчитывается от 1079 до 1081
Если тема интересует, могу отослать к книжке "Математическая смесь". Так есть отдельная глава про по-настоящему большие числа.
Не-не-не-не... Мы реалисты и всякие бесплодные фантазии нас не интересуют. Давайте разобьём нашу Вселенную на кубики со стороной, равной планковской длине, то есть, 10-35 м. Этот элементарный кубик называется планк. Свет будет пролетать это расстояние за 10-43 секунды. Этот элементарный временной промежуток называется хроноквант.
А теперь подсчитаем число состояний нашей Вселенной, начиная от Большого взрыва и заканчивая Большим коллапсом. Можно для начала подсчитать число состояний, как если бы во Вселенной была всего одна частица.
Это делается оч. просто. В следующий момент времени, так называемый хроноквант, центр массы частицы можно обнаружить в одном из 26 планков окрестности или оставшимся на месте. Кубик Рубика вам в помощь.
Итого будет 27 вариантов, они же состояния. Ещё через один хроноквант число состояний увеличится до 273 и так далее. Алгоритм, надеюсь, вы уловили.
Ну и вот, экстраполируем наши рассуждения на 10100 частиц нашей Вселенной. Ой, да хоть и на 101000. Нам не жалко. Таким образом, мы находим самое большое реальное число, которое может нам встретиться. Число состояний нашего Мультиверса. Оно же число параллельных вселенных. Да, с маленькой буквы.
И чтобы не городить степенные башни, мы с Гудстейном придумали тетрацию - гипероператор четвёртого уровня. Для нашего Мультиверса это число навряд ли будет больше
410
В крайнем случае, можем увеличить его до 510. Нам не жалко...)
Это для трехмерной вселенной, но...
Уже не интересно я напишу - вы потом опять уточните.
Вам бы школьный курс подучить. Так, например, понятие энтропии ввёл Клаузиус, Эйлер не вводил число e (первым о нём упоминал Непер), он ввел новое обозначение этого числа (именно "e"). Ну и ещё ряд нестыковок. И, да, чтобы умножить 25 на 25 не нужно ни считать в столбик, ни использовать таблицу логарифмов. Достаточно умножить 2 на 3 и справа дописать 25. Это работает и с другими числами, оканчивающимися на 5.
И последнее
Какой всё-таки век Вы имели ввиду?
Благодарю за замечания, учту после проверки. Я вообще-то не историк науки, но это не снимает ответственности за неточность.
Меня больше порадовало бы Ваше мнение по существу затронутой темы, если Вы в теме.
В теме логарифмов? Логарифм позволил перейти от умножения к сложению, ибо логарифм произведения равен сумме логарифмов. Облегчение расчётов, больше ничего. При современном уровне развития электронно-счетных машин не имеет особо важного значения.
Для борьбы с инфляцией можно вести логарифмические деньги :)
Точно! Если кассиры и бухгалтера вывихнут моск, тоговля остановится.
< Для борьбы с инфляцией....>
В инфляции можно обнаружить энтропию. Так что Ваше предложение можно считать стоящим внимания.
Да, сейчас таблица логарифмов явно или потенциально в каждом калькуляторе.
Но логарифмировние никуда не делось,наооборот расширилось.
Каждый может создать свою систему (таблицу) Поэтому и вопрос о поиске лог. кривой для экономике становится реальным. А может и не надо искать, может достаточно имеющихся двух?
Прям вот так - свою? А Брадиса куда теперь?
Немного подержать, а потом в антикварный магазин. Будет стоить как средневековая икона.
Я долго хранил лог. линейку, потом выбросил, так как движок потерялся.
Ещё в каждом калькуляторе явно или потенциально скрыта таблица умножения. Но это секрет.
Ну конечно же он имеет значение. И именно в экономике, где много разных экспоненциальных вещей.
Экспонента на логарифмической шкале превращается в прямую, иногда и двойна логарифмическая пригоджается.
Но, конечно, никакой мистики там нету. Просто человек неплохо может линейно экстраполировать/интерпоолировать, а с экспонентой интуиция плохо работает, вот и всё.
Да-да. Таблицы Брадиса, то, сё, логарифмическая линейка. Всё очень важно!
Зачем здесь этот парад математической гордости?
< Зачем здесь этот парад >
С моей стороны парада нет. Хочу узнать мнения .
Заодно кто-то вспомнит. Тоже полезно.
Вы просили- позвольте влезть по-существу.
Кмк, сравнивать людей и молекулы, как единичные элементы системы- слишком грубое упрощение.
Дело в том, что (ИМХО, конечно) молекула, как элемент гораздо проще, чем элемент-человек.
Она имеет заведомо сильно меньшее число степеней свободы в системе. Ну, она может перемещаться в системе, динамически контактировать, химически связываться(тогда вообще исчезает , как элемент системы)..... Всё?
А вот человек, в силу природных качеств, кроме первых двух возможностей молекул, имеет массу других степеней свободы в системе. Напр., он имеет воспитание, образование, характер, физические данные( отдельная масса параметров), эмоциональные предпочтения (очень вариабельные в зависимости от условий), возможность развития всех этих качеств. Далее можно рассмотреть общественный аспект разнообразия человеков (партии, родственные общины, сообщества по интересам, профессиям, национальностям, корпоративность, гражданство, отношения с законами, ..) . Ну и ваше любимое- экономические критерии: по уровню доходов, по источникам доходов, по виду траты доходов, по легальности, по сфере деятельности... И это только навскидку...
А теперь посчитайте варианты различных сочетаний этих критериев и получите такие логарифмы!!!!!
Основание по е будет грустно вздыхать от зависти.
Почти всё Вами сказанное не подлежит сомнению.
Почти.
Но остаются очень большие перспективы рассматривать экономику вместе с социльной сферой не путём точных расчётов, что где когда произойдёт, а оценивать и с какой-то вероятностью предвидеть. Это без логарифмов, кажется сделать нельзя.
Перспективный чат детектед! Сим повелеваю - внести запись в реестр самых обсуждаемых за последние 4 часа.
Я вот только не понял: последняя часть — это “шутка смишная” или автор реально не понимает, что вот та самая формула, из которой он высасывает “особость” натурального логарифма S0 = K. lnW0 от формулы S0 = K0. lgW0 будет отличаться только другой константой и более ничем?
P.S. Собственно потому и когда обсуждают, скажем, сложность сортировки, то никто никогда даже не задумывается о том, какое основание использовать: да пофиг, реально же. Главное чтобы всегда одно и то же было и ln A не сравнивали с lg B.
< какое основание использовать: да пофиг, >
Беру Ваш ответ как существенный.
Несколько заставляет задуматься то, что при больших основаниях выход лог. кривой от 1 визуально грубо выглядит.
Дык вы, собственно, и особенность натурального логарифма не углядели потому, что график криво нарисовали: у вас на картинке числа идут от 0 до 13 по вертикали и от 0 до 6 по горизонтали, при этом картинка ещё и неквадратная и вытянута по горизонтали. Чтобы увидеть красивую симметричную картинку (как Wikipedia рисует), масштаб по осям одинаковый нужен:
Но в натуральном логарифме нет никакой мистики: просто его график под 45° ось пересекает и всё, ничего более.
< нет никакой мистики >
Мистику нагнал А.Эйнштейн. Пишут, что очень сильно удивлялся свойству числа 2,7218 как предела прибыли от сложного банковского процента. Да и другие загадки около этого числа...
Спасибо за разъяснение.
Эйнштейн не любил математику: "Математика - лучший способ водить самого себя за нос".
Не раскрыта тема про логарифмов с основанием 2. А она полюбилась некоему Клоду, Шеннону. И стал он измерят информацию битами, а были оные просчитанные с основанием 2.
Поговаривают, что е еще - оптимальное количество состояний некоего элемента состояния, типа да-нет-хз. Но тк встретилися технические трудности с 3-мя состояниями, то люди сделали элементы на основе 2 состояний и пошло.
То есть ваша извилина тугодумает на основаниях 2ва и 3три? Простите, не удержался!
Спасибо за тему ТС и спасибо за комменты! Лучший спсоб дать ребёнку понять науку и смысл вычислений. ~если победит в своей голове текст и комменты, то учиться надо. Если нет, то НЕТ. Универсальный тест, таксказать...
< понять науку и смысл вычислений...>
Чтобы иметь с экономикой разумные отношения надо в первую очередь уловить её суть через образы, в том числе физические и математические. А рассчитывать экономику в целом невозможно, только некоторые процессы.
Уважаемый genri-lezin:
Ну вот я сам когда-то давно учил термодинамику и всякие там социальные науки. В термодинамике мы проходили функции, достигающие экстремумов в системах без потоков энергии. Типа: закрытая система (где нет обмена материей, энергией, и изменений объёма) стремится к состоянию с максимальной энтропией S. Если есть обмен тепловой энергией с окружающим пространством и объём фиксирован, то минимизируется свободная энергия Гельмгольца F = U - TS. Если есть обмен тепловой энергией и фиксировано давление, то минимизируется энергия Гиббса G = H - TS.
Жизнь характеризуется тем что усаживается на всякий потоках материи и энергии и перенаправляет эти потоки для повышения собственной стабильности. Развитие жизни сопровождается появлением экосистем где некоторые живые существа пользуются этими самыми потоками, другие живые существа вместо того чтобы медленно накапливать жирок за счёт этих самых потоков приходят и съедают этих самых живых существ которые накопили; третьи гоняются за вторыми и их поедают снаружи; четвёртые поедают третьих; пятые, не отличаясь умом, скоростью и силой, поедают четвёртых изнутри - итд. Обособленно стоят цивилизации, которые ведут себя сродни многоклеточным организмам, в которых роль клеток выполняют физически отделённые - и иногда весьма друг от друга отдалённые, но тесно друг с другом сотрудничающие организмы.
Соответственно, меня интересует вопрос - какая именно функция стремится к экстремуму в открытой системе в которой присутствуют потоки материи и энергии. Знать бы ответ на этот вопрос - можно было бы определить, каких высот достигнет экосистема, цивилизация, итд.
Но - увы; пока что ответ на этот вопрос я нигде не нашёл.
< какая именно функция стремится к экстремуму в открытой системе >
К экстремуму не знаю, но предел есть. В самом общедоступном образе -- пузырь. В более сложном образе можно увидеть кое-что в рамках обсуждаемой темы.
В другой статье попробую высказать своё мнение.
Новояз, подслушанный в российских научно-административных кругах:
"..наклонить в позу, пригодную для логарифмирования.."