Как и зачем "появилась на свет" тёмная материя
Тёмная материя появилась на свет вовсе не в результате Большого Взрыва, а в университетской столовке на дверях которой висело объявление "Столовая закрывается за 15 минут до своего закрытия" и почему-то на иностранном языке. За столом сидела всё ещё привлекательная феминистка бальзаковского возраста, судя по акценту то ли польского то ли литовского происхожения, и задумчиво возила вилкой в тарелке. Напротив Веры сидел Кент Форд Младший и молча жевал. Кент, к слову сказать, почти всегда молчал - особенно в присутствии Веры - так лучше.
В своих бухгалтерских записях Вера обнаружила недостачу - не хватало массы и притом очень-очень много. И в этом она винила Кента. Сегодня массы не доставало в данных измерений угловых скоростей вращения рукавов спиральной галактики в зависимости от расстояния до её центра. Эту галактику позже назовут Верубиновой Туманностью (The Verubin Nebula) в каком-то очередном американском сериале. И это была не первая проблемная галактика. А точнее, как получалось из данных Кента, почти все галактики были проблемными, особенно спиральные.
Кент Форд Младший занимася фотометрией достаточно давно и не был наивен. Он настаивал на том, что делал всё правильно. Со своей стороны он довёл электростатический фото-мультипликатор в своём спектрометре до совершенства и получил воможность измерять массу удалёных звёзд используя соотношение масса-светимость с очень высокой точностью, а также использовать спектроскопические методы для измерения скоростей. Свои уникальные на тот момент измерения Кент передавал Вере.
Вера выросла в еврейской религиозной семье и с детства свободно читала на древне-египетском. Она прекрасно знала откуда Кеплер взял свои законы и тоже считала эти законы священными. Из третьего закона Кеплера в частности следовало, что если предположить, что основная масса галактики сосредоточена в её центре (galactic bulge), что вполне логично, то орбитальная скорость вещества в диске и в хало должна спадать как квадратный корень от растояния до центра, то есть vcirc = (GM/r)1/2, где М - это масса, а G - гравитационная постоянная. Этот закон великолепно соблюдается для всех известых планетарных систем включая, разумеется, и нашу. Из данных, однако, следовало, что в большинстве случаев орбитальная скорость не только постояна vcirc = const, но может даже и расти с расстоянием от центра. В таком случае получалось, что масса тоже растёт линейно с расстоянием как минимум. Учитывая размеры галактик колличество пропавшей массы потрясало и не поддавалось никакому объяснению.
Многие верят в существование чего-то большого и невидимого, что стоит за спиной мира видимого и тайно им управляет. Так было всегда начиная с древнего Египта и Вавилона. Да и сейчас, если подумать, кто такие Ротшильды с Рокфеллерами как не тёмные силы, которых не видно, но они повсюду. С тёмной материей всё точно также – это по-сути конспирологическая теория. Далее, если предположить, что плотность тёмной материи распределена в галактике как C₀/r², то интеграл от такой плотности в сферической системе координат и даст нужную линейную зависимость. Более того, предполагая, что C₀ есть какая-то функция от r, то можно зафитить любую зависимость величины орбитальной скорости от расстояния, то есть объяснить наблюдаемые кривые вращения.
Английский канал в ясную погоду: Трое в лодке, не считая Махмуда
Уравнения мелкой воды (shallow water equations) вполне себе детерминистические хоть и нелинейные. Детерминизм здесь означает то, что распространение любого возмущения на поверхности воды можно численно промоделировать с очень высокой точностью, чем-то подобным, впрочем, занимается и целая армия предсказателей климата. Но если даже в ясную и безветренную погоду посмотреть на поверхность Английского канала - в простонародье почему-то называемым Ла-Маншем - из корзинки воздушного шара или кабинки дирижабля, то поверхность канала не будет выглядеть идеально гладкой и предсказуемой.
Первое что бросается в глаза, так это богатое разнообразие маленьких волн и волн побольше бегущих с разной скоростью буквально во всех направлениях и интерферирующих между собой. И правда, с высоты волновая картинка выглядит хаотичной. Если, например, лазерной указкой ткнуть в какую-либо точку на поверхности воды, то скорее всего мы не сможем предсказать точно в какой момент времени она подпрыгнет вверх и когда опустится вниз. Хотя понятно, что обязательно когда-то и подпрыгнет и опустится. Модель, которая лучше всего подходит в данном случае, так это стохастическое описание уровня воды как случайного во времени поля (a random field).
Более того, если мысленно провести линию по поверхности воды из точки А в точку В выбрав её, например, как пересечение поверхности воды и перпендикулярной ей плоскости, то длина такой линии (в каждый момент времени и в среднем тоже) будет заведомо больше, чем длина лазерного луча из А в В. А насколько больше - это зависит от статистических характеристик данного случайного поля и от расстояния. При достаточно больших расстояниях вклад шума не должен быть существенным. Так, например, длина экватора на сфере с "зашумлённой поверхностью” должна стремиться к значению длины экватора на идеальной сфере при увеличении радиуса, если, конечно, уровень шума фиксирован.
Опять посмотрев вниз в бинокль и приглядевшись мы вдруг замечаем резиновую надувную лодку с мигрантами следующую из Кале́ видимо к английскому побережью. У лодки заглох мотор. Пока остальные возились с мотором Махмуд сортировал рис, целый мешок которого они отбили в жёсткой поножовщине с какими-то азиатами в порту Кале́. Рис оказался поражён грибком и здоровые зёрнышки следовало отобрать. Махмуд выуживал из мешка годные зёрнышки и аккуратно складывал их в горку на перевёрнутую картонную коробку. Лодку слегка покачивало на волнах. Махмуда мучила изжога от тушёной кошки с грибами, которую он съел в подпольном китайском ресторане незадолго до отплытия из Кале́ и ему приходилось прилагать немало усилий чтобы сконцентрироваться.
Горка риса разъезжалась в разные стороны и всё меньше и меньше напоминала Гауссиан. Более того в ней стали появляться другие горбики и она действительно начинала смахивать на гистограммы Шноля с какого боку на неё не посмотри. Такие отдельные горбики обычно говорят о нескольких случайных процессах наложенных друг на друга. Наверное где-то за горизонтом на круизном лайнере началась дискотека, а может это вызванно приближающейся стаей вечно голодных гено-модифицированных пирано-акул – живущих в холодной солёной воде, жрущих даже резину, и выведенных по заказу правительства Великобритании специально для борьбы с мигрантами.
Гистограммы Шноля говорят, прочем, о том же - наша Земля плывёт в океане пространства-времени до краёв наполненым космическим шумом. Именно космос скорее всего и является истинным источником хаоса. Музыка небесных сфер при повторном прослушивании оказалась рваным панком.
Стохастика
Казалось бы, чего общего в бирживых спекуляциях, обменном курсе валют и мелкой ряби галактического пространства-времени? Однако общее есть - всё это стохастические процессы которые, соответственно, описываются стохастическими дифференциальными уравнениями в основе которых лежит формула Итô (Kiyosi Itô, японец).
Если взять пространственное изменение координаты какой-нибудь частицы со временем, то это изменение может содержать вполне себе детерминистический дрейф (drift term), благодаря, например, потоку несущему эту частицу, и случайные хаотичные изменения траектории. Если хаотичные изменения носят характер Броуновского движения, то это Итô процесс, который также часто называют Винеровским (Norbert Wiener). Математически, изменение случайной величины X можно представить в виде dX = b(X,t)dt + σ(X,t)dB, где первый член с b – дрейф/дрифт, а второй - броуновское движение. Если с дрифтом всё понятно, то второй член с dB следует пояснить.
Выберем к примеру дискретную переменную W принимающую значения 1 и -1 случайным образом за один временной тик. Из неё можно построить условно непрерывную случайную величину B совокупив W с dt. Колмогоров в своё время изучая турбулентность обнаружил (1940), что среднее значение квадрата разности подобных случайных величин ведёт себя как (B’ - B)2 ∼ |t’ – t |n–1, где n появляется из энергетического спектра процесса ∼|ω|-n и удовлетворяет условию: 1 < n < 3. Полагая n = 2 мы получаем Броуновское движение.
Далее зададимся вопросом: а как будет вести себя функция от случайной величины X(t) и времени t? Возьмём какую-то функцию f(X,t), разложим её в ряд Тейлора и подставим туда Итô процесс dX. Далее, учтём свойства броуновского движения, а именно то, что dB⋅ dB = dt, и оставим в разложении члены только первого порядка малости. Таким образом мы получим дифференциальное уравнение по времени для функции f в котором кроме дрифта будут присутствовать чисто стохастический член с dB и дополнительный член появляющийся из условия dB⋅ dB = dt, что, как не трудно догадаться судя по σσT (если σ – матрица, и σ2 - если скаляр), соответствует ковариации. Коэффициент при dt в этом члене будет в общем виде содержать смешанную производную второго порядка от f, то есть, таким образом без дрифта уравнение сводится к уравнению диффузии. Как видим, в отличии от “обычного” дифференциального уравнения (когда dB = 0) стохастическое содержит дополнительные члены и поэтому ведёт себя более хитро и порой даже вероломно. Это уравнение можно формально проинтегрировать и получить знаменитую формулу Итô.
Конечно тут можно бросить карты на стол и вскочив закричать:
– Позвольте-позвольте! Причём тут японцы! Это же уравнение Фоккера-Планка! Это обман и шулерство!
В целом, конечно, зерно истины здесь есть - за азиатами нужен глаз да глаз. Но в защиту Итô всё же можно сказать, что это именно он разработал формализм и технику математических манипуляций с такими процессами (Itô calculus), что удобно. Тем более формула Итô содержит и чисто стохастический член которого нет ни у Фоккера-Планка ни у Колмогорова, что тоже полезно для численного моделирования. Но самое главное это то, что с помощью формализма Итô можно получать (и решать) стохастические уравнения для гораздо более широкого класса функций, чем это изначально предполагало уравнение Фоккера-Планка (его, правда, потом "расширили и углубили" как раз на основе формализма Итô, но функция распределения по определению не может быть отрицательной хотя бы потому, что с её помощью вычисляются вероятности). Так, например, Итô формализм позволяет написать уравнения для синуса и косинуса (или комплексной экспоненты) как функций случайных величин, или, что более значимо для нас, для скалярного произведения случайных векторов - компонент метрического тензора.
Во многих случаях представляют интерес уравнения для математических ожиданий функций от случайных величин. Это тоже можно сделать: применяя оператор мат-ожидания к формуле Итô мы получаем формулу “врага народа” Дынкина в которой по понятным причинам отсутствуют члены с dB и которая действительно очень похожа на Фоккера-Планка, но как и в случае с Итô обоснована для более широкого класса функций. Разумеется, везде вместо времени может быть использован и другой параметр такой как, например, длина.
Галактический шум
Возмём какую-нибудь галактику, желательно спиральную так как они все долбанутые в отличии, например, от эллиптических. Среди последних тоже есть свои девианты, но их поведение не идёт ни в какое сравнение со поведением спиральных. Далее, введём сферическую систему координат с центром в ядре спирального ушлёпка и рассмотрим следующую метрику:
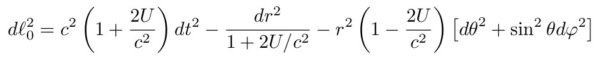
где U - гравитационный потенциал тусовки звёзд в центре галактики равный -GM/r, а M - суммарная масса. Эта метрика очень похожа на Шварцшильдовскую и это не случайно. Однако, в данном случае масса размазана в пространстве и никакого горизонта событий данная метрика не предполагает. К тому же она приближенная, то есть хорошо работает только вдали от центра галактики. При удалении от центра потенциал быстро спадает и метрика сдувается в метрику Минковского, а уравнения движения становятся Ньютоновскими - они выводятся из компонент метрического тензора. А почему Ньютоновскими? - потому что при скоростях в несколько десятков и сотен километров в секунду движение материи нерелятивистское. Это именно то, что предполагала Вера и всё остальные. И мы предположим.
Далее представим радиальную координату r как случайную величину dX = dr + σdB, где σ – вариация шума случайного поля гравитационных волн и прочих гравитационных неоднородностей. Так как в метрику входит r2, то рассмотрим функцию f(r) = r2 как функцию от случайной величины X. Далее, из формулы Итô, а также из Итô-изометрии, которая нам понадобится для усреднения результата, а в частности члена с B2, мы получим среднее значение в виде: <r>2 = r2 + σ2r. Вроде бы результат на первый взгляд неинтересный. И так ясно, что по колдобинам и ухабам расстояние больше, чем по идеальной прямой. Однако, в квадрате расстояния <r> появилась линейная зависимость от r, что весьма любопытно. К чему это ведёт мы обсудим чуть позже. Тот же результат можно получить и из формулы Дынкина несколько более простым путём.
Более того, если мы допустим, что σ меняется в зависимости от r достаточно медленно по сравнению с броуновским процессом B, то в принципе можем применить метод à la Лапласа и посчитать интегралы приближенно. Тогда будет вполне законно использовать среднее значение <r>2 = r2(1 + σ2/r) с σ-ой “умеренно” зависящей от r, что развязывает нам руки. Будем считать также, что σ2/r << 1. Это допущение позволит нам не искать уравнения движения в изменившейся метрике пространства-времени, а воспользоваться Ньютоновскими законами рассматривая σ2/r как малое возмущение.
Навскидку отметим следующее. Во-первых, множитель (1 ± σ2/r) вносит дополнительный вклад в кривизну пространства-времени. То есть, наша Вселенная ещё кривее, чем кажется, особенно в зашумлённых областях. Вдали от них всё более менее устаканивается, но, возможно, не полностью. Во-вторых, дополнительная кривизна неоднородна в пространстве. Естественно предположить, что галактики и их скопления более шумные, чем межгалактическое пространство. Более того, если допустить зависимость σ ещё и от времени (а почему бы и нет?), то можно, кстати, по аналогии космической погодой (space weather) ввести понятие погоды галактической. Ну и галактического климата разумеется!
Законы Кеплера для галактических украинцев
Сведущие люди говорят, что в центре каждой галактики затаилась чёрная дыра. Что ж, может быть. Но в любом случае её Шварцшильдовский радиус настолько мал по сравнению с размерами галактики, что искривлением пространства-времени, которое она вносит, можно смело пренебречь на огромных галактических просторах. Суммарный гравитационный потенциал звёзд тусующихся в центре гораздо более существенен. Но и он спадает с расстоянием тоже достаточно быстро при удалении от центра чтобы заметно искривить пространство-время, а в центр мы не полезем - незачем. Однако, с шумом всё может быть иначе (по крайней мере гистограммы Шноля об этом недвусмысленно говорят). Он может быть повсюду.
А теперь забудем про плоское пространство-время Минковского и попробуем сконструировать свою метрику которая более-менее разумно описывала бы данные наблюдений не впадая в "ересь тёмной материи". Мы уже знаем, что собственная длина окружности длиннее той, что видит удалённый наблюдатель в (1 + σ2/r)1/2 раз. Поэтому квадрат этого множителя войдёт в угловую часть метрики. Далее, собственный радиус тоже будет длиннее (интеграл от этого множителя). Соответствующую компоненту метрического тензора мы запишем приближенно как 1 / (1 - σ2/r) по аналогии со Шварцшильдовской. Далее, если мы хотим (а мы хотим!), чтобы наша метрика удовлетворяла уравнениям Эйнштейна, то мы должны ввести временную компоненту метрического тензора как (1 - σ2/r). То есть, в зашумлённой области время течёт медленнее, а это уже весьма любопытно. В результате с точностью до членов первого порядка малости получим:
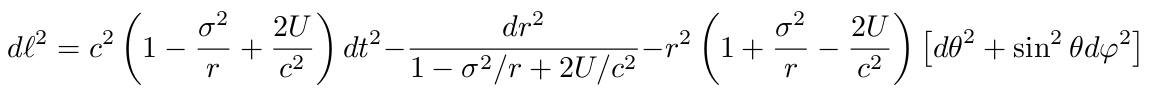
где ℓ - “улучшенное” расстояние в пространстве-времени. Как и раньше пренебрежём гравитационным потенциалом U вдали от центра и будем считать, что уравнения движения Ньютоновские, что в данном случае то же самое, что и Кеплеровские.
Эта метрика справедлива для стационарного поля. В реальности, конечно, гравитационное поле в галактике нестационарно и наверняка ведёт себя более сложным образом и было бы интересно узнать как именно. Однако, для наших целей стационарной метрики вполне достаточно предполагая, что все устаканилось и орбитальные скорости звёзд и их скоплений от времени почти не зависят по крайней мере вдали от центра. То есть, мы говорим о разумном приближении.
Изменение компонент метрического тензора автоматически приводит к изменению геодезических. Уравнения геодезических выражаются через коэффициенты связности Кристоффеля, которые в свою очередь содержат производные компонент метрического тензора. Изогнутые геодезические для света в данном случае приводят к эффекту увеличительного стекла. Однако, считая σ2/r << 1 мы пренебрежём этим эффектом вдали от звёздной тусовки балджа галактики. А центр выглядит больше чем есть и без нас - гравитационного потенциала там для этого вполне достаточно.
Мы знаем, что на окраинах далёких галактик живут украинцы. Зададимся вопросом, а что если для наблюдателя - галактического украинца, летящего вместе с какой-нибудь звездой достаточно далеко от центра “всё хорошо” и третий закон Кеплера для него выполняеся? А именно для круговой орбиты закон работает: ρdψ/dτ = C0/ρ1/2, где ρ - собственное радиальное расстояние, ψ - собственный угол, то что галактический украинец измеряет непосредственно "на месте", τ - собственное время (у него наверняка есть часы - у наших звёздонавтов они постоянно пропадают. Кстати, в прошлый раз аборигены спёрли кофемолку. Наши долго пи...нали ногами их вождя, но кофемолку так и не нашли.), C0 - константа, а ρdψ/dτ – собственная круговая орбитальная скорость, обзовём её wcirc.
Пересчитаем все собственные величины в абсолютные (координатные) - в те, которые использует удалённый наблюдатель за пределами галактики. Для этого нам нашей метрики и сказаного выше вполне достаточно. Далее потребуем, чтобы для удалённого наблюдателя орбитальная скорость звёзд vcirc должна быть постоянной, то есть это то, что мы видим и что так потрясло Веру (кстати, Талли и Фишера не очень потрясло – всё померили без истерики и опубликовали). Это можно сделать собрав все члены зависящие от σ2 и r в коэффициент перед vcirc = rdϕ/dt, где r, ϕ и время t - абсолютные. Тогда мы получим f(σ,r)vcirc = const. А так как vcirc постояна, то и f(σ,r) тоже. Для положительной σ2 условие f = const выполняется не для всех r. Введём параметер R0 - максимальный радиус, который может быть равен радиусу диска галактики или нескольким таким радиусам, и приравняем f к его квадратному корню (всё что дальше R0 не обязанно подчиняться f = const). Полученное уравнение нетрудно разрешить относительно σ2/r даже после пол-бутылки хорошего скотча. В результате получаем σ2/r для радиуса R0, например, в 100 килопарсек в таком виде:
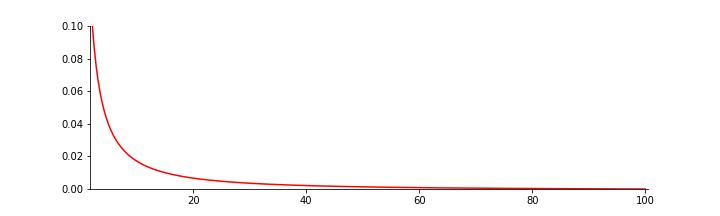
Поясним в двух словах, что же мы имеем. Итак, эффект замедления времени проявляется как "оптический эффект” замедления орбитального вращения звёзд и их скоплений при движении от края к центру галактики. В результате удалённый наблюдатель видит плоские кривые вращения, хотя для аборигенов всё вращается как надо. Во-вторых, звёзды которые ближе к центру выглядят слегка голубее для галактических украинцев, чем, скажем, для англичан. Это вызванно гравитационным красным смещением в результате замедления течения времени. Однако, так как вариация гравитационного шума сравнительно умеренная вдали от центра, то и красное смещение весьма небольшое. В-третьих, решение асимптотическое и вблизи центра не работает. Там “рулит” не шум, а суммарный гравитационный потенциал скопления звёзд. Но мы в центр и не лезли, тем более там не соблюдается видимое постоянство орбитальной скорости - то есть, не очень-то и надо туда лезть. В-четвёртых, всё это шутка, в которой, возможно, есть только доля шутки. Но самое главное это в-пятых: тёмная материя - тоже шутка, но несмешная и с бородой.






Комментарии
Да, как-то так.
Для того чтобы не было всяких там дурацких ЧД, ТМ и ТЭ, и вообще всяких там тёмных сил, надо признать один простейший постулат:
Источником гравитации служит не материя, она лишь реагирует на гравитационный потенциал пространства, и в ней гравитация индуцируется.
ситуация аналогичная металлическим опилкам в магнитном поле. Самт опилки изначально размагничены, но реагируют на магнитный поток и благодаря своей ферромагнитности сами становятся проводником и источником магнитного потока...
Ну и появляются всякие рисунки япобв магнитных полей.
На самом деле это враньё, потому что опилки показывают результирующую картинку взаимодействия исходного магнитного поля и магнитного поля индуцированного в опилках.
С гравитацией тоже самое. Видимые формы туманностей, галактик и звёзд, это лишь отображение результирующего гравиполя от сложения исходного гравиполя в пространстве и "скатившегося" в эти воронки барионнлго вещества, которые сами стало источником и проводником гравиполя...
Другая аналогия, дшарики пенопласта на поверхности воды или земли, будут показывать фому вихрей жидкости или воздуха...
Мощщщно.
А ведь это заявка. ВладиславЛ нервно почесывается.
Заявка? На что?
тут мамомомта обычно расчесывают, а Владислав в этом плане скала!
Spinor на лит.премию имени Бумса тянет, я бы сказал
Если не секрет, что именно понравилось?)
Кое что заценить сложно, поскольку Левич и Ландлившиц привезены скорее как память. Контрабандой. Учебники запрещено вывозить. Урмат сдали в мукулатуру Мой предел сейчас общий курс.
Мой предел сейчас общий курс.
Стиль Иона Тихого напоминает.
Это как? Серьёзно?
Из Узбекистана. Бешенные штрафы. Но я кое что вывезла. Повезло, что контейнер им влом вскрывать было для проверки. И книги старше 50 лет нельзя. Культурные ценности. Так что 2 тонны книг на макулатуру. В том числе учебники. Ещё тонну желающим раздали. Довезла с полтонны. В общем на пару икеевских Билли.
Удивительно! А разве правительство или там университеты закупить то, что нужно не могут? А интернет на что? Весь Ландавщиц есть в свободном доступе в любом формате.
Я ваш пустой коммент внизу удалю?
Могут всё. И есть до сих пор. Общалась с преподами ТашГу. Просто законы такие.
Удаляйте. Я сначала не там ответить нажала.
Эти люди - наш потенциал. Узбекистан, Англия, Америка... Все русские стремятся в Россию...
И это нормально. Подобное стремится к подобному... Айзек Ньютон просил Ивана Грозного предоставить ему российское гражданство...
Об этом мало кому известно... И Джеймс Максвелл тоже просил... )
Да не только русские. Узбеки и татары с образованием и советским менталитетом тоже в Россию едут. Кто то в Европу и Штаты.
Спинор не признаёт замедления времени. Что же касается тёмной материи, то это и без него понятно... Впрочем...
Впрочем, не будем распыляцца... Остановимся пока на времени... Пока... )
Ньютон не знал Ивана. Он мог Петра только о чём-то просить. Но на самом деле всё было как раз наоборот. Это молодой Пётр ездил к Ньютону в Кэмбридж слушать его лекции под предлогом учиться якобы корабельному делу. Мы понимаем, что Голландия тогда была английской провинцией и визы не требовались. А центр Петербурга Пётр срисовал с Лондона.
Увлекательно , но сильно сложно для меня)
Хорошо быть умным.. эххх
статья как научпоп информация-ну так себе
потому как методически не выдержана.
имеющих необходимый физ.-мат. уровень для понимания написанного тут (на этом ресурсе)-с гулькин нос.
для остальных интересующихся (заметное число посетителей данного ресурса, хотя и не большинство)-слишком заумная и стебная.
для квалифицированного большинства (50%+1 чел) посетителей АШ, статья-инфомусор, написанный русскими буквами на непонятном языке и с туманными целями.
гораздо интересней и правильней было бы использование стиля изложения и языка а-ля Дробышевский (тот , правда, по биологии/палеонтологии специалист).
тогда б -зашло.
хотя местами научный стеб и извивы мысли- годные, да...
Это не научпроп. Я просвещать никого не собирался. Научпропа и без меня полно.
ну тогда вы попытались засунуть круглый вал в квадратное отверстие.
Что ж, засунул так засунул.
неа,
не получилось впихнуть невпихуемое
Я не старался, что получилось, то получилось.
Может тогда квадратный вал в круглое отверстие, не?
Вот и Сэры Геи на АШ маршируют.
Тёмную материю можно купить в любом мелкооптовом магазине тканей и фурнитуры. Недорого.
А тёмную энергию качают нефтяники, и даже придумали для него специальное короткое слово.
Это только по-русски звучит похоже.
Ну ее нафиг ту физику. Путь одна.. темная.
Я вот другим сейчас на ночь увлекся:
Уже минут 15 выдерживаю без всхрапываний!
+100 500! АффтАр, жги!
Так то прикольно, конечно, одно осталось непонятно - куда галактика то делась ?
Неужели на Орионе ?) (MIB)
Взорвали случайно.
Закон есть, а вот откуда планетарные, да и галактические системы изначально получили крутящий момент, никто не объяснил.
Те, что не получили или недополучили схлопнулись.
Для возникновения вихря (спиральной галактики) нужен поток, протекающий через сечение с изменяющейся метрикой, без потока (направленного движения) и препятствий на пути потока завихрений нет. Результат мы видим, хотя бы со стороны - плоская спиральная галактика, но что за поток придал веществу форму и вращение галактики? Закон всемирного тяготения может объяснить орбитальные движения, но не может объяснить его возникновение. Как газопылевое облако сжимаясь, приобрело момент вращения и сплющилось в диск? Для солнечной системы центр диска в конце концов превратился в звезду, а остатки диска в планеты, система изначально имеет момент вращения, но откуда она его получила? Что её раскрутило?
Угловой момент сохраняется. Поэтому при сжимании система будет всё сильнее и сильнее раскручиваться. А изначально это может быть просто флуктуация. Вообще-то трудно представить себе какую-либо систему (пылевое облако) совсем без момента.
Всегда хотел узнать, почему галактики в разных плоскостях и крутятся каждая в своей плоскости?
По идее если все вылетели из одной точки - центра Вселенной, у каждого края от центра они должны быть почти параллельны друг дружке?
Они ниоткуда не вылетали, а сформировались из вещества, которое охлаждалось с расширением пространства-времени. Тем более, как считается, у Вселенной нет центра.
А где тогда произошёл БВ? Опять же, расширяться, по идее, она должна во все стороны. Во все стороны от какого места?
Опять же, по Фридману Вселенная это поверхность сферы в многомерном пространстве-времени (если воспользоваться вложением). А у поверхности нет центра. И нет границ. И она всё время раздувется. Более того, теория Большого Взрыва противоречит существованию чёрных дыр. Либо одно - либо другое. Либо ни того, ни другого.
Давеча один человек сообщил под строгим секретом - что тёмная материя и антивещество лежит за границей скорости света - и нужно построить корапь , достичь скорости , открыть форточку и отщипнуть и того и другого . И даже указал как - дескать - нужно сложить пространство время как полотенце - и тогда , вода нам как земля , и тогда - нам экипаж семья. В ютубах блистает лекционно донатно. В целом всегда всё одобряю, сурово насупивЪ айброу..
Хороший юмор. В стиле Лема.
шизофазией попахивает, а так интересно! половину только осилил, после обеда дочитаю
Шизофазия - это что такое? Вы доктор? Поясните.
Ну нет уж, написать такой текст и спрашивать!!! Сами, всё сами
Не дохтур я, окадемиев не кончал, в ваших ландонах не бывал, из колхозу мы, так что адьёс амиго
"Шизофазия" это фраза "звезды выглядят голубее из-за красного смещения"
Это просто праздник какой-то!
И темную энергию туда же, - а то в XX веке
астрологиякосмология стала вся ad hoc и только, а потом начались поиски Ноева ковчега.Перспективный чат детектед! Сим повелеваю - внести запись в реестр самых обсуждаемых за последние 4 часа.
прекрасная задница?
Страницы